Gaussian Mean Field Variational Inference can Overestimate Predictive Variance

Mean Field Variational Inference (MFVI) is widely understood to underestimate posterior variance. By analysing conjugate Bayesian Linear Regression (BLR), we show that this characterization is incomplete: while MFVI underestimates the variance in parameter space, it can overestimate the predictive variance compared to the exact posterior. We show that if the MFVI posterior underestimates predictive variances in some directions, it necessarily overestimates them in others. Crucially, this overestimation occurs in directions where the training data concentrates. This leads to the surprising result that, for a test point drawn from the training distribution, MFVI's expected predictive variance exceeds that of the exact posterior. We demonstrate a pathological case of this effect, where the MFVI posterior fails to reduce predictive variance compared to the prior on in distribution data. We connect these results to the Cold Posterior Effect, arguing that varying the temperature can correct this overestimation, yielding predictions closer to those of the exact posterior. We validate our theory on synthetic and real-world regression tasks.

Standard Acquisition Is Sufficient for Asynchronous Bayesian Optimization

Asynchronous Bayesian optimization is widely used for gradient-free optimization in domains with independent parallel experiments and varying evaluation times. Existing methods posit that standard acquisitions lead to redundant and repeated queries, proposing complex solutions to enforce diversity in queries. Challenging this fundamental premise, we show that methods, like the Upper Confidence Bound, can in fact achieve theoretical guarantees essentially equivalent to those of sequential Thompson sampling. A conceptual analysis of asynchronous Bayesian optimization reveals that existing works neglect intermediate posterior updates, which we find to be generally sufficient to avoid redundant queries. Further investigation shows that by penalizing busy locations, diversity-enforcing methods can over-explore in asynchronous settings, reducing their performance. Our extensive experiments demonstrate that simple standard acquisition functions match or outperform purpose-built asynchronous methods across synthetic and real-world tasks.

Mixed-Output Gaussian Process Latent Variable Models

This work develops a Bayesian non-parametric approach to signal separation where the signals may vary according to latent variables. Our key contribution is to augment Gaussian Process Latent Variable Models (GPLVMs) to incorporate the case where each data point comprises the weighted sum of a known number of pure component signals, observed across several input locations. Our framework allows the use of a range of priors for the weights of each observation. This flexibility enables us to represent use cases including sum-to-one constraints for estimating fractional makeup, and binary weights for classification. Our contributions are particularly relevant to spectroscopy, where changing conditions may cause the underlying pure component signals to vary from sample to sample. To demonstrate the applicability to both spectroscopy and other domains, we consider several applications: a near-infrared spectroscopy data set with varying temperatures, a simulated data set for identifying flow configuration through a pipe, and a data set for determining the type of rock from its reflectance.

Practical Path-based Bayesian Optimization

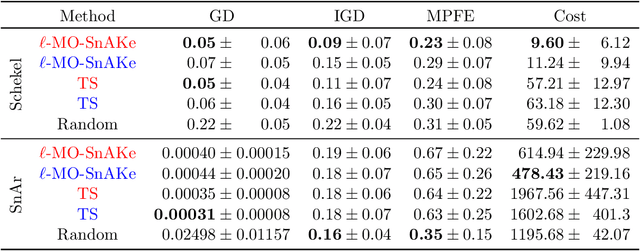
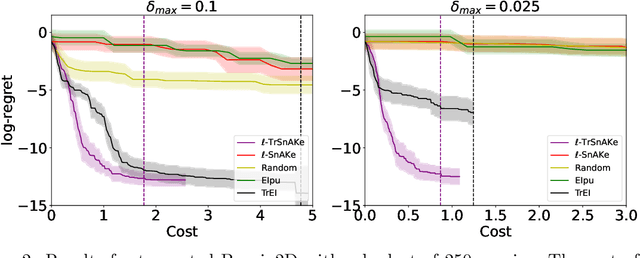
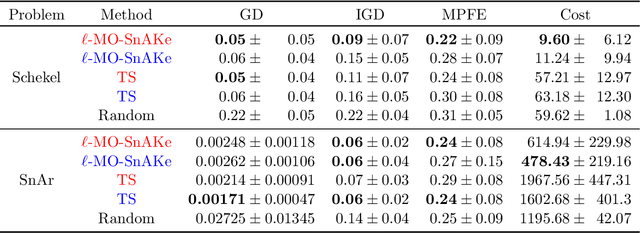
There has been a surge in interest in data-driven experimental design with applications to chemical engineering and drug manufacturing. Bayesian optimization (BO) has proven to be adaptable to such cases, since we can model the reactions of interest as expensive black-box functions. Sometimes, the cost of this black-box functions can be separated into two parts: (a) the cost of the experiment itself, and (b) the cost of changing the input parameters. In this short paper, we extend the SnAKe algorithm to deal with both types of costs simultaneously. We further propose extensions to the case of a maximum allowable input change, as well as to the multi-objective setting.