BoFire: Bayesian Optimization Framework Intended for Real Experiments

Our open-source Python package BoFire combines Bayesian Optimization (BO) with other design of experiments (DoE) strategies focusing on developing and optimizing new chemistry. Previous BO implementations, for example as they exist in the literature or software, require substantial adaptation for effective real-world deployment in chemical industry. BoFire provides a rich feature-set with extensive configurability and realizes our vision of fast-tracking research contributions into industrial use via maintainable open-source software. Owing to quality-of-life features like JSON-serializability of problem formulations, BoFire enables seamless integration of BO into RESTful APIs, a common architecture component for both self-driving laboratories and human-in-the-loop setups. This paper discusses the differences between BoFire and other BO implementations and outlines ways that BO research needs to be adapted for real-world use in a chemistry setting.

System-Aware Neural ODE Processes for Few-Shot Bayesian Optimization

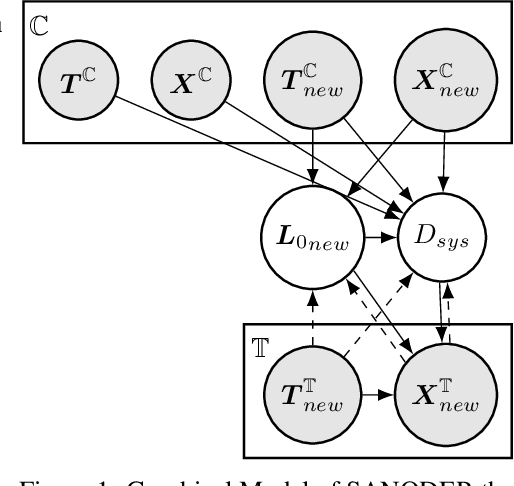
We consider the problem of optimizing initial conditions and timing in dynamical systems governed by unknown ordinary differential equations (ODEs), where evaluating different initial conditions is costly and there are constraints on observation times. To identify the optimal conditions within several trials, we introduce a few-shot Bayesian Optimization (BO) framework based on the system's prior information. At the core of our approach is the System-Aware Neural ODE Processes (SANODEP), an extension of Neural ODE Processes (NODEP) designed to meta-learn ODE systems from multiple trajectories using a novel context embedding block. Additionally, we propose a multi-scenario loss function specifically for optimization purposes. Our two-stage BO framework effectively incorporates search space constraints, enabling efficient optimization of both initial conditions and observation timings. We conduct extensive experiments showcasing SANODEP's potential for few-shot BO. We also explore SANODEP's adaptability to varying levels of prior information, highlighting the trade-off between prior flexibility and model fitting accuracy.

Scalarisation-based risk concepts for robust multi-objective optimisation

Robust optimisation is a well-established framework for optimising functions in the presence of uncertainty. The inherent goal of this problem is to identify a collection of inputs whose outputs are both desirable for the decision maker, whilst also being robust to the underlying uncertainties in the problem. In this work, we study the multi-objective extension of this problem from a computational standpoint. We identify that the majority of all robust multi-objective algorithms rely on two key operations: robustification and scalarisation. Robustification refers to the strategy that is used to marginalise over the uncertainty in the problem. Whilst scalarisation refers to the procedure that is used to encode the relative importance of each objective. As these operations are not necessarily commutative, the order that they are performed in has an impact on the resulting solutions that are identified and the final decisions that are made. This work aims to give an exposition on the philosophical differences between these two operations and highlight when one should opt for one ordering over the other. As part of our analysis, we showcase how many existing risk concepts can be easily integrated into the specification and solution of a robust multi-objective optimisation problem. Besides this, we also demonstrate how one can principally define the notion of a robust Pareto front and a robust performance metric based on our robustify and scalarise methodology. To illustrate the efficacy of these new ideas, we present two insightful numerical case studies which are based on real-world data sets.

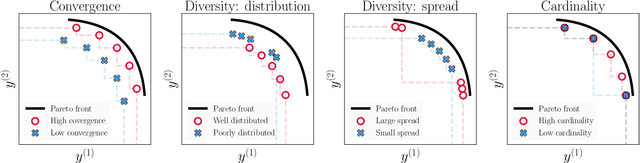
Random Pareto front surfaces

The Pareto front of a set of vectors is the subset which is comprised solely of all of the best trade-off points. By interpolating this subset, we obtain the optimal trade-off surface. In this work, we prove a very useful result which states that all Pareto front surfaces can be explicitly parametrised using polar coordinates. In particular, our polar parametrisation result tells us that we can fully characterise any Pareto front surface using the length function, which is a scalar-valued function that returns the projected length along any positive radial direction. Consequently, by exploiting this representation, we show how it is possible to generalise many useful concepts from linear algebra, probability and statistics, and decision theory to function over the space of Pareto front surfaces. Notably, we focus our attention on the stochastic setting where the Pareto front surface itself is a stochastic process. Among other things, we showcase how it is possible to define and estimate many statistical quantities of interest such as the expectation, covariance and quantile of any Pareto front surface distribution. As a motivating example, we investigate how these statistics can be used within a design of experiments setting, where the goal is to both infer and use the Pareto front surface distribution in order to make effective decisions. Besides this, we also illustrate how these Pareto front ideas can be used within the context of extreme value theory. Finally, as a numerical example, we applied some of our new methodology on a real-world air pollution data set.

Transition Constrained Bayesian Optimization via Markov Decision Processes

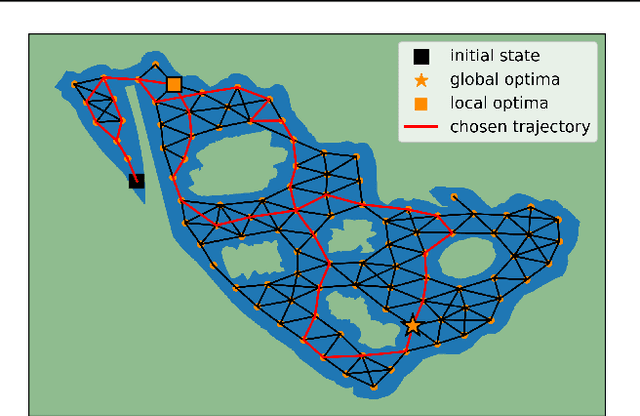
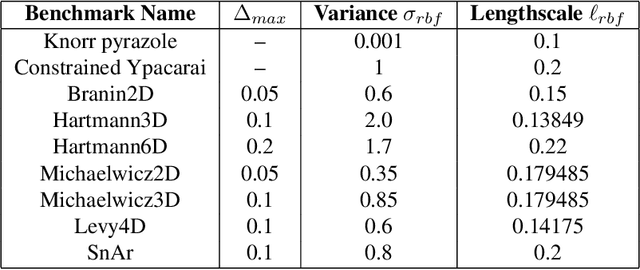
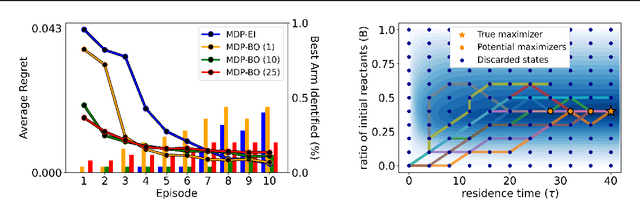
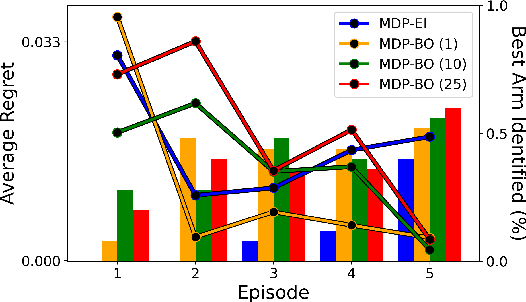
Bayesian optimization is a methodology to optimize black-box functions. Traditionally, it focuses on the setting where you can arbitrarily query the search space. However, many real-life problems do not offer this flexibility; in particular, the search space of the next query may depend on previous ones. Example challenges arise in the physical sciences in the form of local movement constraints, required monotonicity in certain variables, and transitions influencing the accuracy of measurements. Altogether, such transition constraints necessitate a form of planning. This work extends Bayesian optimization via the framework of Markov Decision Processes, iteratively solving a tractable linearization of our objective using reinforcement learning to obtain a policy that plans ahead over long horizons. The resulting policy is potentially history-dependent and non-Markovian. We showcase applications in chemical reactor optimization, informative path planning, machine calibration, and other synthetic examples.

Practical Path-based Bayesian Optimization

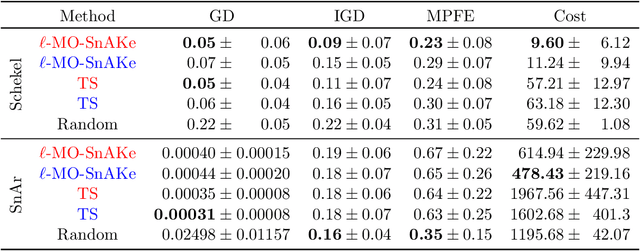
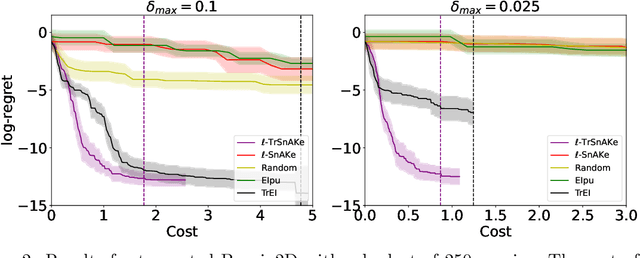
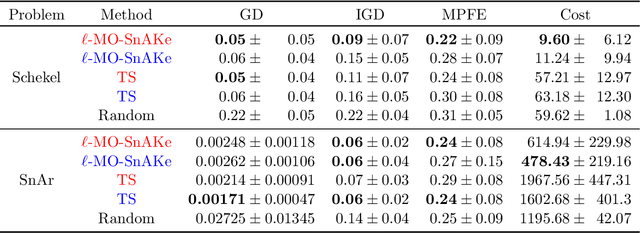
There has been a surge in interest in data-driven experimental design with applications to chemical engineering and drug manufacturing. Bayesian optimization (BO) has proven to be adaptable to such cases, since we can model the reactions of interest as expensive black-box functions. Sometimes, the cost of this black-box functions can be separated into two parts: (a) the cost of the experiment itself, and (b) the cost of changing the input parameters. In this short paper, we extend the SnAKe algorithm to deal with both types of costs simultaneously. We further propose extensions to the case of a maximum allowable input change, as well as to the multi-objective setting.

Multi-Objective Optimization Using the R2 Utility

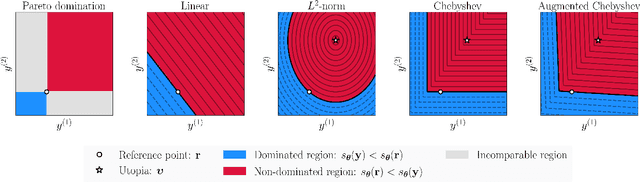
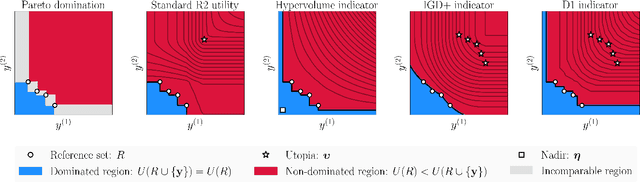
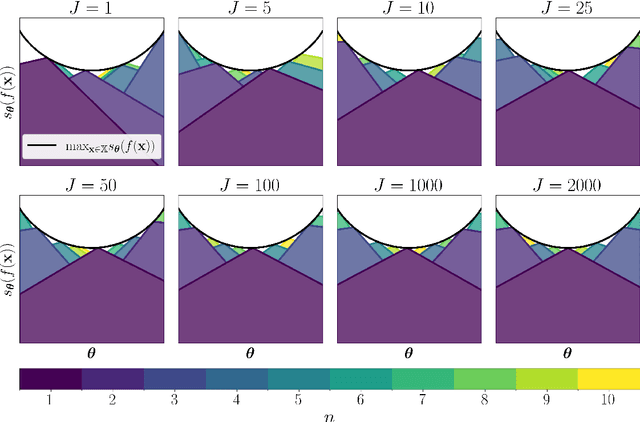
The goal of multi-objective optimization is to identify a collection of points which describe the best possible trade-offs between the multiple objectives. In order to solve this vector-valued optimization problem, practitioners often appeal to the use of scalarization functions in order to transform the multi-objective problem into a collection of single-objective problems. This set of scalarized problems can then be solved using traditional single-objective optimization techniques. In this work, we formalise this convention into a general mathematical framework. We show how this strategy effectively recasts the original multi-objective optimization problem into a single-objective optimization problem defined over sets. An appropriate class of objective functions for this new problem is the R2 utility function, which is defined as a weighted integral over the scalarized optimization problems. We show that this utility function is a monotone and submodular set function, which can be optimised effectively using greedy optimization algorithms. We analyse the performance of these greedy algorithms both theoretically and empirically. Our analysis largely focusses on Bayesian optimization, which is a popular probabilistic framework for black-box optimization.

Combining Multi-Fidelity Modelling and Asynchronous Batch Bayesian Optimization

Bayesian Optimization is a useful tool for experiment design. Unfortunately, the classical, sequential setting of Bayesian Optimization does not translate well into laboratory experiments, for instance battery design, where measurements may come from different sources and their evaluations may require significant waiting times. Multi-fidelity Bayesian Optimization addresses the setting with measurements from different sources. Asynchronous batch Bayesian Optimization provides a framework to select new experiments before the results of the prior experiments are revealed. This paper proposes an algorithm combining multi-fidelity and asynchronous batch methods. We empirically study the algorithm behavior, and show it can outperform single-fidelity batch methods and multi-fidelity sequential methods. As an application, we consider designing electrode materials for optimal performance in pouch cells using experiments with coin cells to approximate battery performance.

Joint Entropy Search for Multi-objective Bayesian Optimization

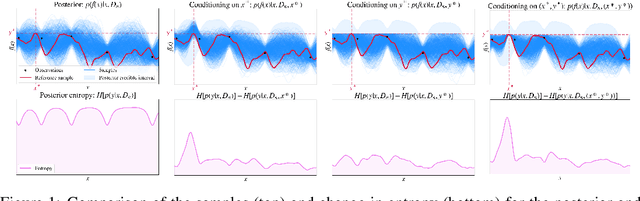
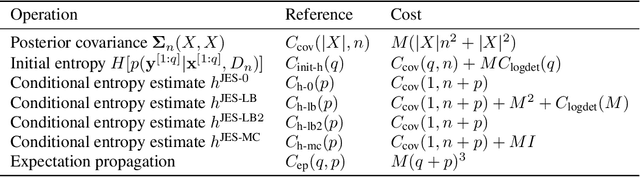
Many real-world problems can be phrased as a multi-objective optimization problem, where the goal is to identify the best set of compromises between the competing objectives. Multi-objective Bayesian optimization (BO) is a sample efficient strategy that can be deployed to solve these vector-valued optimization problems where access is limited to a number of noisy objective function evaluations. In this paper, we propose a novel information-theoretic acquisition function for BO called Joint Entropy Search (JES), which considers the joint information gain for the optimal set of inputs and outputs. We present several analytical approximations to the JES acquisition function and also introduce an extension to the batch setting. We showcase the effectiveness of this new approach on a range of synthetic and real-world problems in terms of the hypervolume and its weighted variants.

Tree ensemble kernels for Bayesian optimization with known constraints over mixed-feature spaces

Tree ensembles can be well-suited for black-box optimization tasks such as algorithm tuning and neural architecture search, as they achieve good predictive performance with little to no manual tuning, naturally handle discrete feature spaces, and are relatively insensitive to outliers in the training data. Two well-known challenges in using tree ensembles for black-box optimization are (i) effectively quantifying model uncertainty for exploration and (ii) optimizing over the piece-wise constant acquisition function. To address both points simultaneously, we propose using the kernel interpretation of tree ensembles as a Gaussian Process prior to obtain model variance estimates, and we develop a compatible optimization formulation for the acquisition function. The latter further allows us to seamlessly integrate known constraints to improve sampling efficiency by considering domain-knowledge in engineering settings and modeling search space symmetries, e.g., hierarchical relationships in neural architecture search. Our framework performs as well as state-of-the-art methods for unconstrained black-box optimization over continuous/discrete features and outperforms competing methods for problems combining mixed-variable feature spaces and known input constraints.