Scalarisation-based risk concepts for robust multi-objective optimisation

Robust optimisation is a well-established framework for optimising functions in the presence of uncertainty. The inherent goal of this problem is to identify a collection of inputs whose outputs are both desirable for the decision maker, whilst also being robust to the underlying uncertainties in the problem. In this work, we study the multi-objective extension of this problem from a computational standpoint. We identify that the majority of all robust multi-objective algorithms rely on two key operations: robustification and scalarisation. Robustification refers to the strategy that is used to marginalise over the uncertainty in the problem. Whilst scalarisation refers to the procedure that is used to encode the relative importance of each objective. As these operations are not necessarily commutative, the order that they are performed in has an impact on the resulting solutions that are identified and the final decisions that are made. This work aims to give an exposition on the philosophical differences between these two operations and highlight when one should opt for one ordering over the other. As part of our analysis, we showcase how many existing risk concepts can be easily integrated into the specification and solution of a robust multi-objective optimisation problem. Besides this, we also demonstrate how one can principally define the notion of a robust Pareto front and a robust performance metric based on our robustify and scalarise methodology. To illustrate the efficacy of these new ideas, we present two insightful numerical case studies which are based on real-world data sets.

Random Pareto front surfaces

The Pareto front of a set of vectors is the subset which is comprised solely of all of the best trade-off points. By interpolating this subset, we obtain the optimal trade-off surface. In this work, we prove a very useful result which states that all Pareto front surfaces can be explicitly parametrised using polar coordinates. In particular, our polar parametrisation result tells us that we can fully characterise any Pareto front surface using the length function, which is a scalar-valued function that returns the projected length along any positive radial direction. Consequently, by exploiting this representation, we show how it is possible to generalise many useful concepts from linear algebra, probability and statistics, and decision theory to function over the space of Pareto front surfaces. Notably, we focus our attention on the stochastic setting where the Pareto front surface itself is a stochastic process. Among other things, we showcase how it is possible to define and estimate many statistical quantities of interest such as the expectation, covariance and quantile of any Pareto front surface distribution. As a motivating example, we investigate how these statistics can be used within a design of experiments setting, where the goal is to both infer and use the Pareto front surface distribution in order to make effective decisions. Besides this, we also illustrate how these Pareto front ideas can be used within the context of extreme value theory. Finally, as a numerical example, we applied some of our new methodology on a real-world air pollution data set.

Multi-Objective Optimization Using the R2 Utility

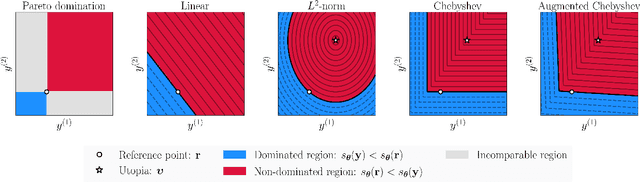
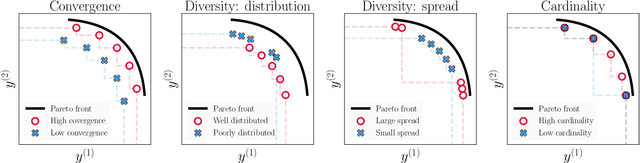
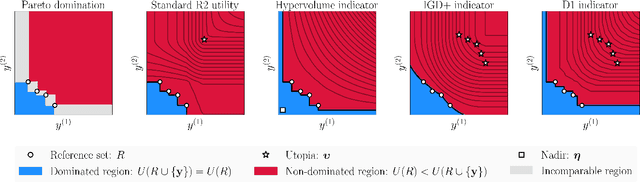
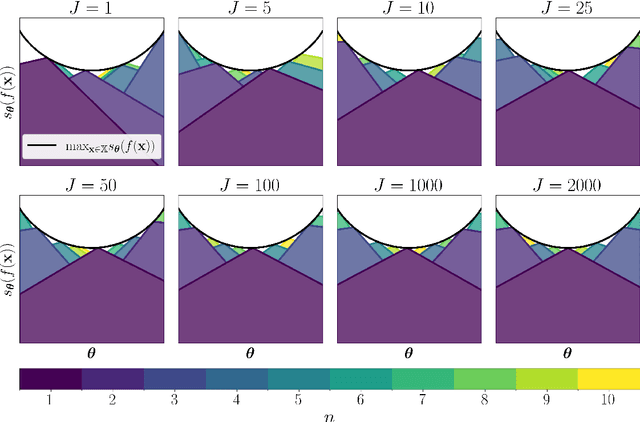
The goal of multi-objective optimization is to identify a collection of points which describe the best possible trade-offs between the multiple objectives. In order to solve this vector-valued optimization problem, practitioners often appeal to the use of scalarization functions in order to transform the multi-objective problem into a collection of single-objective problems. This set of scalarized problems can then be solved using traditional single-objective optimization techniques. In this work, we formalise this convention into a general mathematical framework. We show how this strategy effectively recasts the original multi-objective optimization problem into a single-objective optimization problem defined over sets. An appropriate class of objective functions for this new problem is the R2 utility function, which is defined as a weighted integral over the scalarized optimization problems. We show that this utility function is a monotone and submodular set function, which can be optimised effectively using greedy optimization algorithms. We analyse the performance of these greedy algorithms both theoretically and empirically. Our analysis largely focusses on Bayesian optimization, which is a popular probabilistic framework for black-box optimization.

Joint Entropy Search for Multi-objective Bayesian Optimization

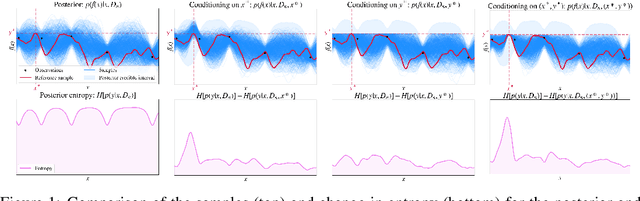
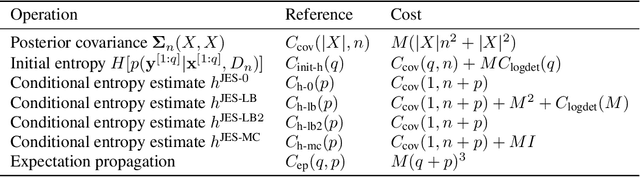
Many real-world problems can be phrased as a multi-objective optimization problem, where the goal is to identify the best set of compromises between the competing objectives. Multi-objective Bayesian optimization (BO) is a sample efficient strategy that can be deployed to solve these vector-valued optimization problems where access is limited to a number of noisy objective function evaluations. In this paper, we propose a novel information-theoretic acquisition function for BO called Joint Entropy Search (JES), which considers the joint information gain for the optimal set of inputs and outputs. We present several analytical approximations to the JES acquisition function and also introduce an extension to the batch setting. We showcase the effectiveness of this new approach on a range of synthetic and real-world problems in terms of the hypervolume and its weighted variants.