BoFire: Bayesian Optimization Framework Intended for Real Experiments

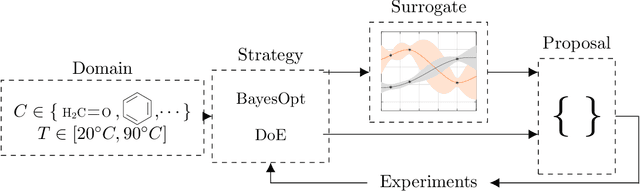
Our open-source Python package BoFire combines Bayesian Optimization (BO) with other design of experiments (DoE) strategies focusing on developing and optimizing new chemistry. Previous BO implementations, for example as they exist in the literature or software, require substantial adaptation for effective real-world deployment in chemical industry. BoFire provides a rich feature-set with extensive configurability and realizes our vision of fast-tracking research contributions into industrial use via maintainable open-source software. Owing to quality-of-life features like JSON-serializability of problem formulations, BoFire enables seamless integration of BO into RESTful APIs, a common architecture component for both self-driving laboratories and human-in-the-loop setups. This paper discusses the differences between BoFire and other BO implementations and outlines ways that BO research needs to be adapted for real-world use in a chemistry setting.

Scalarisation-based risk concepts for robust multi-objective optimisation

Robust optimisation is a well-established framework for optimising functions in the presence of uncertainty. The inherent goal of this problem is to identify a collection of inputs whose outputs are both desirable for the decision maker, whilst also being robust to the underlying uncertainties in the problem. In this work, we study the multi-objective extension of this problem from a computational standpoint. We identify that the majority of all robust multi-objective algorithms rely on two key operations: robustification and scalarisation. Robustification refers to the strategy that is used to marginalise over the uncertainty in the problem. Whilst scalarisation refers to the procedure that is used to encode the relative importance of each objective. As these operations are not necessarily commutative, the order that they are performed in has an impact on the resulting solutions that are identified and the final decisions that are made. This work aims to give an exposition on the philosophical differences between these two operations and highlight when one should opt for one ordering over the other. As part of our analysis, we showcase how many existing risk concepts can be easily integrated into the specification and solution of a robust multi-objective optimisation problem. Besides this, we also demonstrate how one can principally define the notion of a robust Pareto front and a robust performance metric based on our robustify and scalarise methodology. To illustrate the efficacy of these new ideas, we present two insightful numerical case studies which are based on real-world data sets.

Random Pareto front surfaces

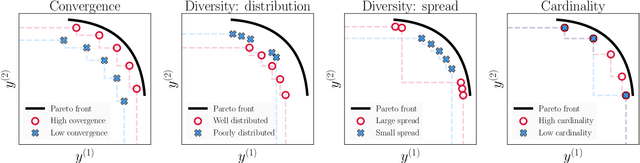
The Pareto front of a set of vectors is the subset which is comprised solely of all of the best trade-off points. By interpolating this subset, we obtain the optimal trade-off surface. In this work, we prove a very useful result which states that all Pareto front surfaces can be explicitly parametrised using polar coordinates. In particular, our polar parametrisation result tells us that we can fully characterise any Pareto front surface using the length function, which is a scalar-valued function that returns the projected length along any positive radial direction. Consequently, by exploiting this representation, we show how it is possible to generalise many useful concepts from linear algebra, probability and statistics, and decision theory to function over the space of Pareto front surfaces. Notably, we focus our attention on the stochastic setting where the Pareto front surface itself is a stochastic process. Among other things, we showcase how it is possible to define and estimate many statistical quantities of interest such as the expectation, covariance and quantile of any Pareto front surface distribution. As a motivating example, we investigate how these statistics can be used within a design of experiments setting, where the goal is to both infer and use the Pareto front surface distribution in order to make effective decisions. Besides this, we also illustrate how these Pareto front ideas can be used within the context of extreme value theory. Finally, as a numerical example, we applied some of our new methodology on a real-world air pollution data set.

Multi-Objective Optimization Using the R2 Utility

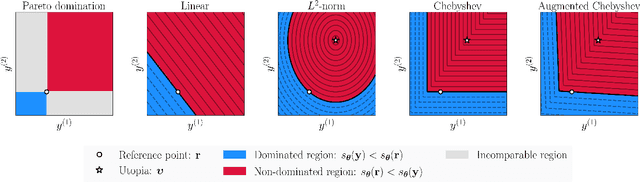
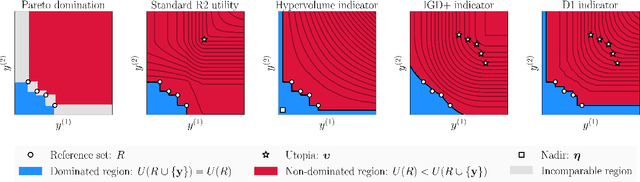
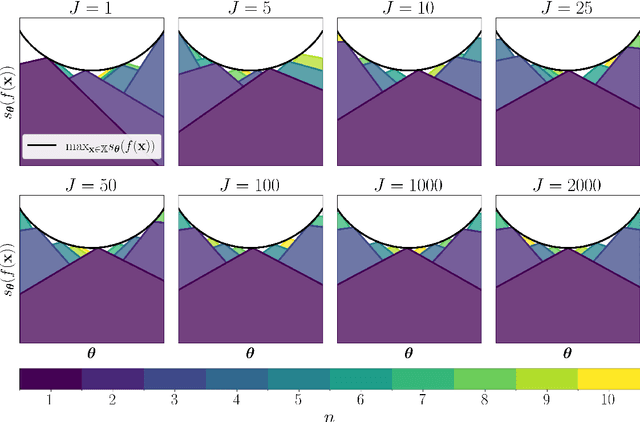
The goal of multi-objective optimization is to identify a collection of points which describe the best possible trade-offs between the multiple objectives. In order to solve this vector-valued optimization problem, practitioners often appeal to the use of scalarization functions in order to transform the multi-objective problem into a collection of single-objective problems. This set of scalarized problems can then be solved using traditional single-objective optimization techniques. In this work, we formalise this convention into a general mathematical framework. We show how this strategy effectively recasts the original multi-objective optimization problem into a single-objective optimization problem defined over sets. An appropriate class of objective functions for this new problem is the R2 utility function, which is defined as a weighted integral over the scalarized optimization problems. We show that this utility function is a monotone and submodular set function, which can be optimised effectively using greedy optimization algorithms. We analyse the performance of these greedy algorithms both theoretically and empirically. Our analysis largely focusses on Bayesian optimization, which is a popular probabilistic framework for black-box optimization.

Tree ensemble kernels for Bayesian optimization with known constraints over mixed-feature spaces

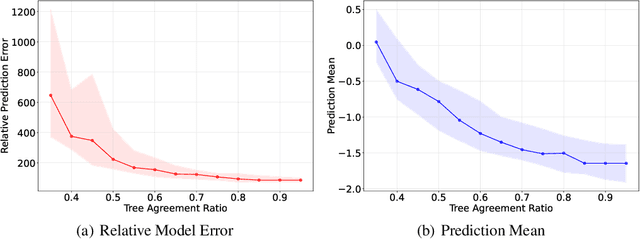
Tree ensembles can be well-suited for black-box optimization tasks such as algorithm tuning and neural architecture search, as they achieve good predictive performance with little to no manual tuning, naturally handle discrete feature spaces, and are relatively insensitive to outliers in the training data. Two well-known challenges in using tree ensembles for black-box optimization are (i) effectively quantifying model uncertainty for exploration and (ii) optimizing over the piece-wise constant acquisition function. To address both points simultaneously, we propose using the kernel interpretation of tree ensembles as a Gaussian Process prior to obtain model variance estimates, and we develop a compatible optimization formulation for the acquisition function. The latter further allows us to seamlessly integrate known constraints to improve sampling efficiency by considering domain-knowledge in engineering settings and modeling search space symmetries, e.g., hierarchical relationships in neural architecture search. Our framework performs as well as state-of-the-art methods for unconstrained black-box optimization over continuous/discrete features and outperforms competing methods for problems combining mixed-variable feature spaces and known input constraints.

Multi-Objective Constrained Optimization for Energy Applications via Tree Ensembles

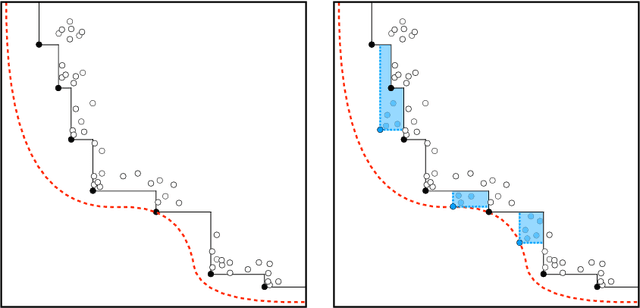
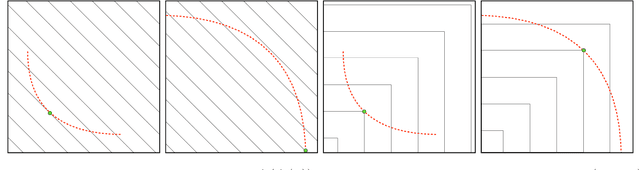
Energy systems optimization problems are complex due to strongly non-linear system behavior and multiple competing objectives, e.g. economic gain vs. environmental impact. Moreover, a large number of input variables and different variable types, e.g. continuous and categorical, are challenges commonly present in real-world applications. In some cases, proposed optimal solutions need to obey explicit input constraints related to physical properties or safety-critical operating conditions. This paper proposes a novel data-driven strategy using tree ensembles for constrained multi-objective optimization of black-box problems with heterogeneous variable spaces for which underlying system dynamics are either too complex to model or unknown. In an extensive case study comprised of synthetic benchmarks and relevant energy applications we demonstrate the competitive performance and sampling efficiency of the proposed algorithm compared to other state-of-the-art tools, making it a useful all-in-one solution for real-world applications with limited evaluation budgets.

ENTMOOT: A Framework for Optimization over Ensemble Tree Models

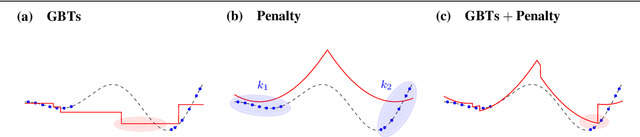
Gradient boosted trees and other regression tree models perform well in a wide range of real-world, industrial applications. These tree models (i) offer insight into important prediction features, (ii) effectively manage sparse data, and (iii) have excellent prediction capabilities. Despite their advantages, they are generally unpopular for decision-making tasks and black-box optimization, which is due to their difficult-to-optimize structure and the lack of a reliable uncertainty measure. ENTMOOT is our new framework for integrating (already trained) tree models into larger optimization problems. The contributions of ENTMOOT include: (i) explicitly introducing a reliable uncertainty measure that is compatible with tree models, (ii) solving the larger optimization problems that incorporate these uncertainty aware tree models, (iii) proving that the solutions are globally optimal, i.e. no better solution exists. In particular, we show how the ENTMOOT approach allows a simple integration of tree models into decision-making and black-box optimization, where it proves as a strong competitor to commonly-used frameworks.

Mixed-Integer Convex Nonlinear Optimization with Gradient-Boosted Trees Embedded

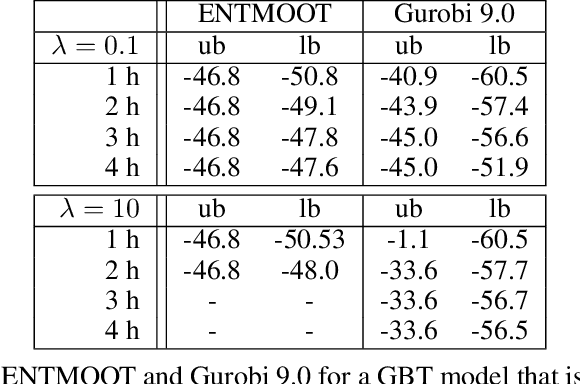
Decision trees usefully represent sparse, high dimensional and noisy data. Having learned a function from this data, we may want to thereafter integrate the function into a larger decision-making problem, e.g., for picking the best chemical process catalyst. We study a large-scale, industrially-relevant mixed-integer nonlinear nonconvex optimization problem involving both gradient-boosted trees and penalty functions mitigating risk. This mixed-integer optimization problem with convex penalty terms broadly applies to optimizing pre-trained regression tree models. Decision makers may wish to optimize discrete models to repurpose legacy predictive models, or they may wish to optimize a discrete model that particularly well-represents a data set. We develop several heuristic methods to find feasible solutions, and an exact, branch-and-bound algorithm leveraging structural properties of the gradient-boosted trees and penalty functions. We computationally test our methods on concrete mixture design instance and a chemical catalysis industrial instance.