Tree ensemble kernels for Bayesian optimization with known constraints over mixed-feature spaces

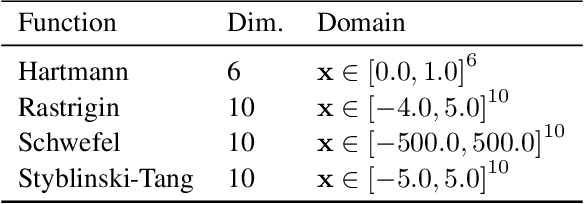
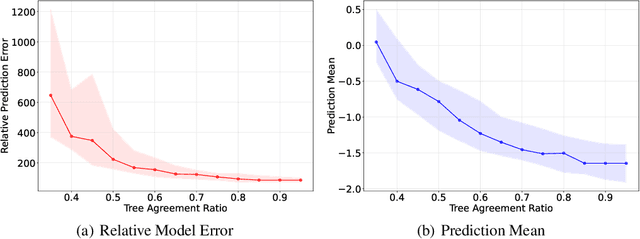
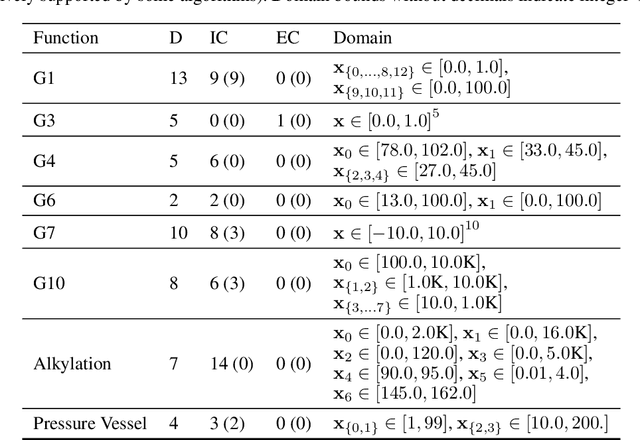
Tree ensembles can be well-suited for black-box optimization tasks such as algorithm tuning and neural architecture search, as they achieve good predictive performance with little to no manual tuning, naturally handle discrete feature spaces, and are relatively insensitive to outliers in the training data. Two well-known challenges in using tree ensembles for black-box optimization are (i) effectively quantifying model uncertainty for exploration and (ii) optimizing over the piece-wise constant acquisition function. To address both points simultaneously, we propose using the kernel interpretation of tree ensembles as a Gaussian Process prior to obtain model variance estimates, and we develop a compatible optimization formulation for the acquisition function. The latter further allows us to seamlessly integrate known constraints to improve sampling efficiency by considering domain-knowledge in engineering settings and modeling search space symmetries, e.g., hierarchical relationships in neural architecture search. Our framework performs as well as state-of-the-art methods for unconstrained black-box optimization over continuous/discrete features and outperforms competing methods for problems combining mixed-variable feature spaces and known input constraints.

Multi-Objective Constrained Optimization for Energy Applications via Tree Ensembles

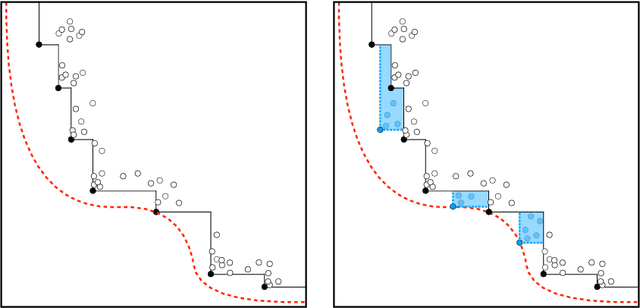
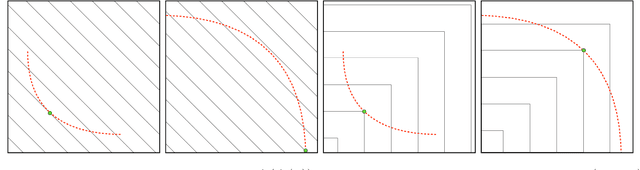
Energy systems optimization problems are complex due to strongly non-linear system behavior and multiple competing objectives, e.g. economic gain vs. environmental impact. Moreover, a large number of input variables and different variable types, e.g. continuous and categorical, are challenges commonly present in real-world applications. In some cases, proposed optimal solutions need to obey explicit input constraints related to physical properties or safety-critical operating conditions. This paper proposes a novel data-driven strategy using tree ensembles for constrained multi-objective optimization of black-box problems with heterogeneous variable spaces for which underlying system dynamics are either too complex to model or unknown. In an extensive case study comprised of synthetic benchmarks and relevant energy applications we demonstrate the competitive performance and sampling efficiency of the proposed algorithm compared to other state-of-the-art tools, making it a useful all-in-one solution for real-world applications with limited evaluation budgets.

ENTMOOT: A Framework for Optimization over Ensemble Tree Models

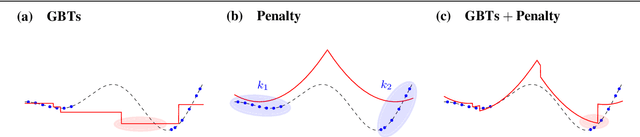
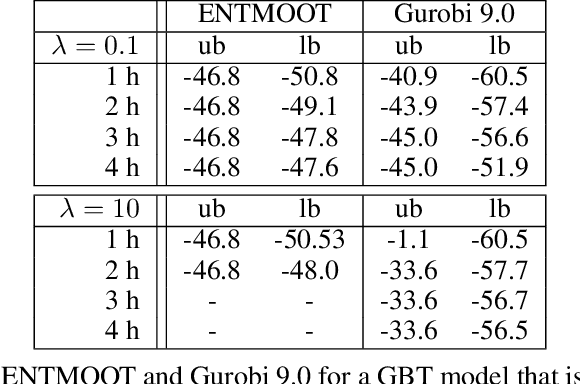
Gradient boosted trees and other regression tree models perform well in a wide range of real-world, industrial applications. These tree models (i) offer insight into important prediction features, (ii) effectively manage sparse data, and (iii) have excellent prediction capabilities. Despite their advantages, they are generally unpopular for decision-making tasks and black-box optimization, which is due to their difficult-to-optimize structure and the lack of a reliable uncertainty measure. ENTMOOT is our new framework for integrating (already trained) tree models into larger optimization problems. The contributions of ENTMOOT include: (i) explicitly introducing a reliable uncertainty measure that is compatible with tree models, (ii) solving the larger optimization problems that incorporate these uncertainty aware tree models, (iii) proving that the solutions are globally optimal, i.e. no better solution exists. In particular, we show how the ENTMOOT approach allows a simple integration of tree models into decision-making and black-box optimization, where it proves as a strong competitor to commonly-used frameworks.