ENTMOOT: A Framework for Optimization over Ensemble Tree Models

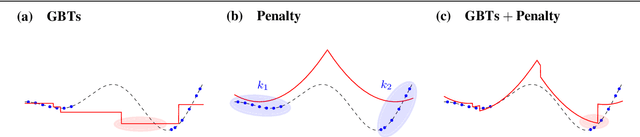
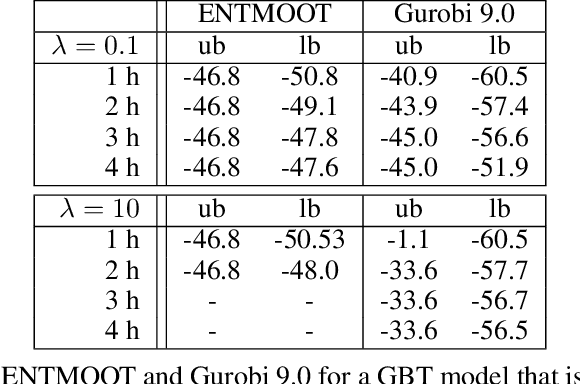
Gradient boosted trees and other regression tree models perform well in a wide range of real-world, industrial applications. These tree models (i) offer insight into important prediction features, (ii) effectively manage sparse data, and (iii) have excellent prediction capabilities. Despite their advantages, they are generally unpopular for decision-making tasks and black-box optimization, which is due to their difficult-to-optimize structure and the lack of a reliable uncertainty measure. ENTMOOT is our new framework for integrating (already trained) tree models into larger optimization problems. The contributions of ENTMOOT include: (i) explicitly introducing a reliable uncertainty measure that is compatible with tree models, (ii) solving the larger optimization problems that incorporate these uncertainty aware tree models, (iii) proving that the solutions are globally optimal, i.e. no better solution exists. In particular, we show how the ENTMOOT approach allows a simple integration of tree models into decision-making and black-box optimization, where it proves as a strong competitor to commonly-used frameworks.

Mixed-Integer Convex Nonlinear Optimization with Gradient-Boosted Trees Embedded

Decision trees usefully represent sparse, high dimensional and noisy data. Having learned a function from this data, we may want to thereafter integrate the function into a larger decision-making problem, e.g., for picking the best chemical process catalyst. We study a large-scale, industrially-relevant mixed-integer nonlinear nonconvex optimization problem involving both gradient-boosted trees and penalty functions mitigating risk. This mixed-integer optimization problem with convex penalty terms broadly applies to optimizing pre-trained regression tree models. Decision makers may wish to optimize discrete models to repurpose legacy predictive models, or they may wish to optimize a discrete model that particularly well-represents a data set. We develop several heuristic methods to find feasible solutions, and an exact, branch-and-bound algorithm leveraging structural properties of the gradient-boosted trees and penalty functions. We computationally test our methods on concrete mixture design instance and a chemical catalysis industrial instance.