Argumentation for Explainable Scheduling (Full Paper with Proofs)

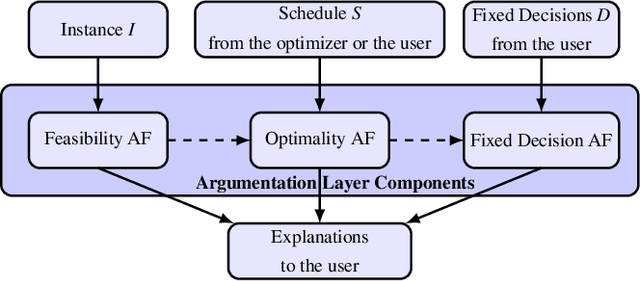
Mathematical optimization offers highly-effective tools for finding solutions for problems with well-defined goals, notably scheduling. However, optimization solvers are often unexplainable black boxes whose solutions are inaccessible to users and which users cannot interact with. We define a novel paradigm using argumentation to empower the interaction between optimization solvers and users, supported by tractable explanations which certify or refute solutions. A solution can be from a solver or of interest to a user (in the context of 'what-if' scenarios). Specifically, we define argumentative and natural language explanations for why a schedule is (not) feasible, (not) efficient or (not) satisfying fixed user decisions, based on models of the fundamental makespan scheduling problem in terms of abstract argumentation frameworks (AFs). We define three types of AFs, whose stable extensions are in one-to-one correspondence with schedules that are feasible, efficient and satisfying fixed decisions, respectively. We extract the argumentative explanations from these AFs and the natural language explanations from the argumentative ones.

Mixed-Integer Convex Nonlinear Optimization with Gradient-Boosted Trees Embedded

Decision trees usefully represent sparse, high dimensional and noisy data. Having learned a function from this data, we may want to thereafter integrate the function into a larger decision-making problem, e.g., for picking the best chemical process catalyst. We study a large-scale, industrially-relevant mixed-integer nonlinear nonconvex optimization problem involving both gradient-boosted trees and penalty functions mitigating risk. This mixed-integer optimization problem with convex penalty terms broadly applies to optimizing pre-trained regression tree models. Decision makers may wish to optimize discrete models to repurpose legacy predictive models, or they may wish to optimize a discrete model that particularly well-represents a data set. We develop several heuristic methods to find feasible solutions, and an exact, branch-and-bound algorithm leveraging structural properties of the gradient-boosted trees and penalty functions. We computationally test our methods on concrete mixture design instance and a chemical catalysis industrial instance.