A stochastic smoothing framework for nonconvex-nonconcave min-sum-max problems with applications to Wasserstein distributionally robust optimization

Applications such as adversarially robust training and Wasserstein Distributionally Robust Optimization (WDRO) can be naturally formulated as min-sum-max optimization problems. While this formulation can be rewritten as an equivalent min-max problem, the summation of max terms introduces computational challenges, including increased complexity and memory demands, which must be addressed. These challenges are particularly evident in WDRO, where existing tractable algorithms often rely on restrictive assumptions on the objective function, limiting their applicability to state-of-the-art machine learning problems such as the training of deep neural networks. This study introduces a novel stochastic smoothing framework based on the \mbox{log-sum-exp} function, efficiently approximating the max operator in min-sum-max problems. By leveraging the Clarke regularity of the max operator, we develop an iterative smoothing algorithm that addresses these computational difficulties and guarantees almost surely convergence to a Clarke/directional stationary point. We further prove that the proposed algorithm finds an $\epsilon$-scaled Clarke stationary point of the original problem, with a worst-case iteration complexity of $\widetilde{O}(\epsilon^{-3})$. Our numerical experiments demonstrate that our approach outperforms or is competitive with state-of-the-art methods in solving the newsvendor problem, deep learning regression, and adversarially robust deep learning. The results highlight that our method yields more accurate and robust solutions in these challenging problem settings.

BoFire: Bayesian Optimization Framework Intended for Real Experiments

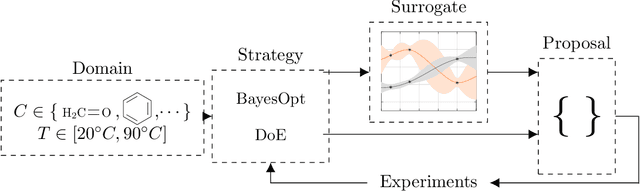
Our open-source Python package BoFire combines Bayesian Optimization (BO) with other design of experiments (DoE) strategies focusing on developing and optimizing new chemistry. Previous BO implementations, for example as they exist in the literature or software, require substantial adaptation for effective real-world deployment in chemical industry. BoFire provides a rich feature-set with extensive configurability and realizes our vision of fast-tracking research contributions into industrial use via maintainable open-source software. Owing to quality-of-life features like JSON-serializability of problem formulations, BoFire enables seamless integration of BO into RESTful APIs, a common architecture component for both self-driving laboratories and human-in-the-loop setups. This paper discusses the differences between BoFire and other BO implementations and outlines ways that BO research needs to be adapted for real-world use in a chemistry setting.

Variance-reduced accelerated methods for decentralized stochastic double-regularized nonconvex strongly-concave minimax problems

In this paper, we consider the decentralized, stochastic nonconvex strongly-concave (NCSC) minimax problem with nonsmooth regularization terms on both primal and dual variables, wherein a network of $m$ computing agents collaborate via peer-to-peer communications. We consider when the coupling function is in expectation or finite-sum form and the double regularizers are convex functions, applied separately to the primal and dual variables. Our algorithmic framework introduces a Lagrangian multiplier to eliminate the consensus constraint on the dual variable. Coupling this with variance-reduction (VR) techniques, our proposed method, entitled VRLM, by a single neighbor communication per iteration, is able to achieve an $\mathcal{O}(\kappa^3\varepsilon^{-3})$ sample complexity under the general stochastic setting, with either a big-batch or small-batch VR option, where $\kappa$ is the condition number of the problem and $\varepsilon$ is the desired solution accuracy. With a big-batch VR, we can additionally achieve $\mathcal{O}(\kappa^2\varepsilon^{-2})$ communication complexity. Under the special finite-sum setting, our method with a big-batch VR can achieve an $\mathcal{O}(n + \sqrt{n} \kappa^2\varepsilon^{-2})$ sample complexity and $\mathcal{O}(\kappa^2\varepsilon^{-2})$ communication complexity, where $n$ is the number of components in the finite sum. All complexity results match the best-known results achieved by a few existing methods for solving special cases of the problem we consider. To the best of our knowledge, this is the first work which provides convergence guarantees for NCSC minimax problems with general convex nonsmooth regularizers applied to both the primal and dual variables in the decentralized stochastic setting. Numerical experiments are conducted on two machine learning problems. Our code is downloadable from https://github.com/RPI-OPT/VRLM.