Using Perturbation to Improve Goodness-of-Fit Tests based on Kernelized Stein Discrepancy

Kernelized Stein discrepancy (KSD) is a score-based discrepancy widely used in goodness-of-fit tests. It can be applied even when the target distribution has an unknown normalising factor, such as in Bayesian analysis. We show theoretically and empirically that the KSD test can suffer from low power when the target and the alternative distribution have the same well-separated modes but differ in mixing proportions. We propose to perturb the observed sample via Markov transition kernels, with respect to which the target distribution is invariant. This allows us to then employ the KSD test on the perturbed sample. We provide numerical evidence that with suitably chosen kernels the proposed approach can lead to a substantially higher power than the KSD test.

A High-dimensional Convergence Theorem for U-statistics with Applications to Kernel-based Testing

We prove a convergence theorem for U-statistics of degree two, where the data dimension $d$ is allowed to scale with sample size $n$. We find that the limiting distribution of a U-statistic undergoes a phase transition from the non-degenerate Gaussian limit to the degenerate limit, regardless of its degeneracy and depending only on a moment ratio. A surprising consequence is that a non-degenerate U-statistic in high dimensions can have a non-Gaussian limit with a larger variance and asymmetric distribution. Our bounds are valid for any finite $n$ and $d$, independent of individual eigenvalues of the underlying function, and dimension-independent under a mild assumption. As an application, we apply our theory to two popular kernel-based distribution tests, MMD and KSD, whose high-dimensional performance has been challenging to study. In a simple empirical setting, our results correctly predict how the test power at a fixed threshold scales with $d$ and the bandwidth.

Joint Entropy Search for Multi-objective Bayesian Optimization

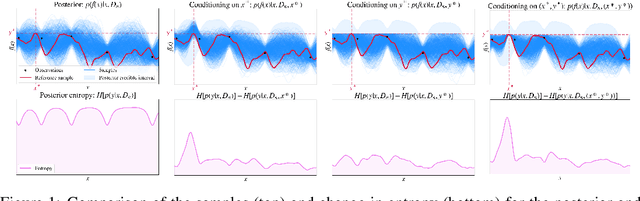
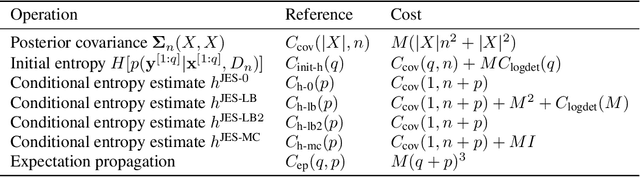
Many real-world problems can be phrased as a multi-objective optimization problem, where the goal is to identify the best set of compromises between the competing objectives. Multi-objective Bayesian optimization (BO) is a sample efficient strategy that can be deployed to solve these vector-valued optimization problems where access is limited to a number of noisy objective function evaluations. In this paper, we propose a novel information-theoretic acquisition function for BO called Joint Entropy Search (JES), which considers the joint information gain for the optimal set of inputs and outputs. We present several analytical approximations to the JES acquisition function and also introduce an extension to the batch setting. We showcase the effectiveness of this new approach on a range of synthetic and real-world problems in terms of the hypervolume and its weighted variants.

Can a latent Hawkes process be used for epidemiological modelling?

Understanding the spread of COVID-19 has been the subject of numerous studies, highlighting the significance of reliable epidemic models. Here, we introduce a novel epidemic model using a latent Hawkes process with temporal covariates for modelling the infections. Unlike other models, we model the reported cases via a probability distribution driven by the underlying Hawkes process. Modelling the infections via a Hawkes process allows us to estimate by whom an infected individual was infected. We propose a Kernel Density Particle Filter (KDPF) for inference of both latent cases and reproduction number and for predicting the new cases in the near future. The computational effort is proportional to the number of infections making it possible to use particle filter type algorithms, such as the KDPF. We demonstrate the performance of the proposed algorithm on synthetic data sets and COVID-19 reported cases in various local authorities in the UK, and benchmark our model to alternative approaches.

BART-based inference for Poisson processes

The effectiveness of Bayesian Additive Regression Trees (BART) has been demonstrated in a variety of contexts including non parametric regression and classification. Here we introduce a BART scheme for estimating the intensity of inhomogeneous Poisson Processes. Poisson intensity estimation is a vital task in various applications including medical imaging, astrophysics and network traffic analysis. Our approach enables full posterior inference of the intensity in a nonparametric regression setting. We demonstrate the performance of our scheme through simulation studies on synthetic and real datasets in one and two dimensions, and compare our approach to alternative approaches.

Joint analysis of clinical risk factors and 4D cardiac motion for survival prediction using a hybrid deep learning network

In this work, a novel approach is proposed for joint analysis of high dimensional time-resolved cardiac motion features obtained from segmented cardiac MRI and low dimensional clinical risk factors to improve survival prediction in heart failure. Different methods are evaluated to find the optimal way to insert conventional covariates into deep prediction networks. Correlation analysis between autoencoder latent codes and covariate features is used to examine how these predictors interact. We believe that similar approaches could also be used to introduce knowledge of genetic variants to such survival networks to improve outcome prediction by jointly analysing cardiac motion traits with inheritable risk factors.