Transition Constrained Bayesian Optimization via Markov Decision Processes

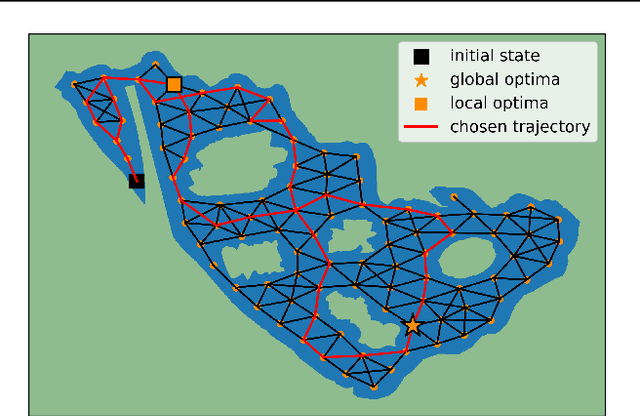
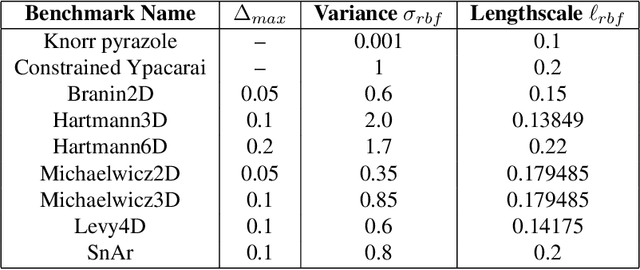
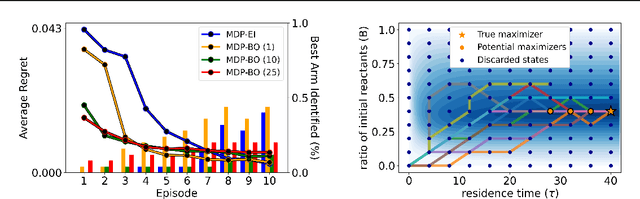
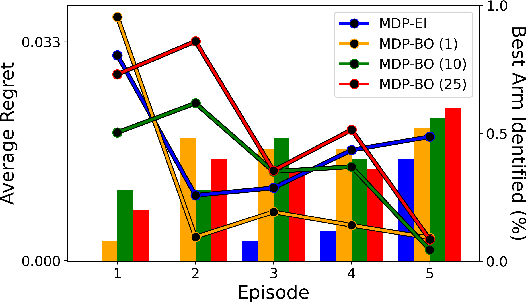
Bayesian optimization is a methodology to optimize black-box functions. Traditionally, it focuses on the setting where you can arbitrarily query the search space. However, many real-life problems do not offer this flexibility; in particular, the search space of the next query may depend on previous ones. Example challenges arise in the physical sciences in the form of local movement constraints, required monotonicity in certain variables, and transitions influencing the accuracy of measurements. Altogether, such transition constraints necessitate a form of planning. This work extends Bayesian optimization via the framework of Markov Decision Processes, iteratively solving a tractable linearization of our objective using reinforcement learning to obtain a policy that plans ahead over long horizons. The resulting policy is potentially history-dependent and non-Markovian. We showcase applications in chemical reactor optimization, informative path planning, machine calibration, and other synthetic examples.

Likelihood Ratio Confidence Sets for Sequential Decision Making

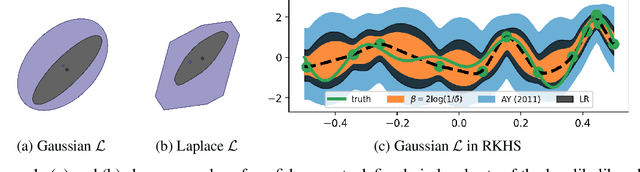
Certifiable, adaptive uncertainty estimates for unknown quantities are an essential ingredient of sequential decision-making algorithms. Standard approaches rely on problem-dependent concentration results and are limited to a specific combination of parameterization, noise family, and estimator. In this paper, we revisit the likelihood-based inference principle and propose to use likelihood ratios to construct any-time valid confidence sequences without requiring specialized treatment in each application scenario. Our method is especially suitable for problems with well-specified likelihoods, and the resulting sets always maintain the prescribed coverage in a model-agnostic manner. The size of the sets depends on a choice of estimator sequence in the likelihood ratio. We discuss how to provably choose the best sequence of estimators and shed light on connections to online convex optimization with algorithms such as Follow-the-Regularized-Leader. To counteract the initially large bias of the estimators, we propose a reweighting scheme that also opens up deployment in non-parametric settings such as RKHS function classes. We provide a non-asymptotic analysis of the likelihood ratio confidence sets size for generalized linear models, using insights from convex duality and online learning. We showcase the practical strength of our method on generalized linear bandit problems, survival analysis, and bandits with various additive noise distributions.

Submodular Reinforcement Learning

In reinforcement learning (RL), rewards of states are typically considered additive, and following the Markov assumption, they are $\textit{independent}$ of states visited previously. In many important applications, such as coverage control, experiment design and informative path planning, rewards naturally have diminishing returns, i.e., their value decreases in light of similar states visited previously. To tackle this, we propose $\textit{submodular RL}$ (SubRL), a paradigm which seeks to optimize more general, non-additive (and history-dependent) rewards modelled via submodular set functions which capture diminishing returns. Unfortunately, in general, even in tabular settings, we show that the resulting optimization problem is hard to approximate. On the other hand, motivated by the success of greedy algorithms in classical submodular optimization, we propose SubPO, a simple policy gradient-based algorithm for SubRL that handles non-additive rewards by greedily maximizing marginal gains. Indeed, under some assumptions on the underlying Markov Decision Process (MDP), SubPO recovers optimal constant factor approximations of submodular bandits. Moreover, we derive a natural policy gradient approach for locally optimizing SubRL instances even in large state- and action- spaces. We showcase the versatility of our approach by applying SubPO to several applications, such as biodiversity monitoring, Bayesian experiment design, informative path planning, and coverage maximization. Our results demonstrate sample efficiency, as well as scalability to high-dimensional state-action spaces.

Active Exploration via Experiment Design in Markov Chains

A key challenge in science and engineering is to design experiments to learn about some unknown quantity of interest. Classical experimental design optimally allocates the experimental budget to maximize a notion of utility (e.g., reduction in uncertainty about the unknown quantity). We consider a rich setting, where the experiments are associated with states in a {\em Markov chain}, and we can only choose them by selecting a {\em policy} controlling the state transitions. This problem captures important applications, from exploration in reinforcement learning to spatial monitoring tasks. We propose an algorithm -- \textsc{markov-design} -- that efficiently selects policies whose measurement allocation \emph{provably converges to the optimal one}. The algorithm is sequential in nature, adapting its choice of policies (experiments) informed by past measurements. In addition to our theoretical analysis, we showcase our framework on applications in ecological surveillance and pharmacology.

Experimental Design for Linear Functionals in Reproducing Kernel Hilbert Spaces

Optimal experimental design seeks to determine the most informative allocation of experiments to infer an unknown statistical quantity. In this work, we investigate the optimal design of experiments for {\em estimation of linear functionals in reproducing kernel Hilbert spaces (RKHSs)}. This problem has been extensively studied in the linear regression setting under an estimability condition, which allows estimating parameters without bias. We generalize this framework to RKHSs, and allow for the linear functional to be only approximately inferred, i.e., with a fixed bias. This scenario captures many important modern applications, such as estimation of gradient maps, integrals, and solutions to differential equations. We provide algorithms for constructing bias-aware designs for linear functionals. We derive non-asymptotic confidence sets for fixed and adaptive designs under sub-Gaussian noise, enabling us to certify estimation with bounded error with high probability.

Diversified Sampling for Batched Bayesian Optimization with Determinantal Point Processes

In Bayesian Optimization (BO) we study black-box function optimization with noisy point evaluations and Bayesian priors. Convergence of BO can be greatly sped up by batching, where multiple evaluations of the black-box function are performed in a single round. The main difficulty in this setting is to propose at the same time diverse and informative batches of evaluation points. In this work, we introduce DPP-Batch Bayesian Optimization (DPP-BBO), a universal framework for inducing batch diversity in sampling based BO by leveraging the repulsive properties of Determinantal Point Processes (DPP) to naturally diversify the batch sampling procedure. We illustrate this framework by formulating DPP-Thompson Sampling (DPP-TS) as a variant of the popular Thompson Sampling (TS) algorithm and introducing a Markov Chain Monte Carlo procedure to sample from it. We then prove novel Bayesian simple regret bounds for both classical batched TS as well as our counterpart DPP-TS, with the latter bound being tighter. Our real-world, as well as synthetic, experiments demonstrate improved performance of DPP-BBO over classical batching methods with Gaussian process and Cox process models.

Sensing Cox Processes via Posterior Sampling and Positive Bases

We study adaptive sensing of Cox point processes, a widely used model from spatial statistics. We introduce three tasks: maximization of captured events, search for the maximum of the intensity function and learning level sets of the intensity function. We model the intensity function as a sample from a truncated Gaussian process, represented in a specially constructed positive basis. In this basis, the positivity constraint on the intensity function has a simple form. We show how an minimal description positive basis can be adapted to the covariance kernel, non-stationarity and make connections to common positive bases from prior works. Our adaptive sensing algorithms use Langevin dynamics and are based on posterior sampling (\textsc{Cox-Thompson}) and top-two posterior sampling (\textsc{Top2}) principles. With latter, the difference between samples serves as a surrogate to the uncertainty. We demonstrate the approach using examples from environmental monitoring and crime rate modeling, and compare it to the classical Bayesian experimental design approach.

Data Summarization via Bilevel Optimization

The increasing availability of massive data sets poses a series of challenges for machine learning. Prominent among these is the need to learn models under hardware or human resource constraints. In such resource-constrained settings, a simple yet powerful approach is to operate on small subsets of the data. Coresets are weighted subsets of the data that provide approximation guarantees for the optimization objective. However, existing coreset constructions are highly model-specific and are limited to simple models such as linear regression, logistic regression, and $k$-means. In this work, we propose a generic coreset construction framework that formulates the coreset selection as a cardinality-constrained bilevel optimization problem. In contrast to existing approaches, our framework does not require model-specific adaptations and applies to any twice differentiable model, including neural networks. We show the effectiveness of our framework for a wide range of models in various settings, including training non-convex models online and batch active learning.

Efficient Pure Exploration for Combinatorial Bandits with Semi-Bandit Feedback

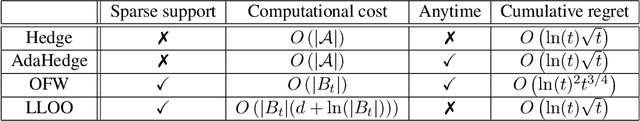
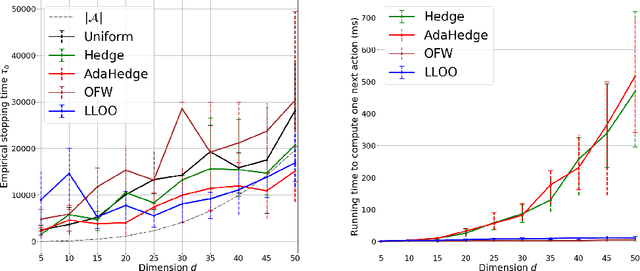
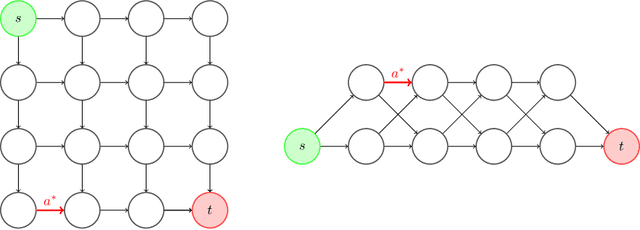
Combinatorial bandits with semi-bandit feedback generalize multi-armed bandits, where the agent chooses sets of arms and observes a noisy reward for each arm contained in the chosen set. The action set satisfies a given structure such as forming a base of a matroid or a path in a graph. We focus on the pure-exploration problem of identifying the best arm with fixed confidence, as well as a more general setting, where the structure of the answer set differs from the one of the action set. Using the recently popularized game framework, we interpret this problem as a sequential zero-sum game and develop a CombGame meta-algorithm whose instances are asymptotically optimal algorithms with finite time guarantees. In addition to comparing two families of learners to instantiate our meta-algorithm, the main contribution of our work is a specific oracle efficient instance for best-arm identification with combinatorial actions. Based on a projection-free online learning algorithm for convex polytopes, it is the first computationally efficient algorithm which is asymptotically optimal and has competitive empirical performance.

Coresets via Bilevel Optimization for Continual Learning and Streaming

Coresets are small data summaries that are sufficient for model training. They can be maintained online, enabling efficient handling of large data streams under resource constraints. However, existing constructions are limited to simple models such as k-means and logistic regression. In this work, we propose a novel coreset construction via cardinality-constrained bilevel optimization. We show how our framework can efficiently generate coresets for deep neural networks, and demonstrate its empirical benefits in continual learning and in streaming settings.