The Catechol Benchmark: Time-series Solvent Selection Data for Few-shot Machine Learning

Machine learning has promised to change the landscape of laboratory chemistry, with impressive results in molecular property prediction and reaction retro-synthesis. However, chemical datasets are often inaccessible to the machine learning community as they tend to require cleaning, thorough understanding of the chemistry, or are simply not available. In this paper, we introduce a novel dataset for yield prediction, providing the first-ever transient flow dataset for machine learning benchmarking, covering over 1200 process conditions. While previous datasets focus on discrete parameters, our experimental set-up allow us to sample a large number of continuous process conditions, generating new challenges for machine learning models. We focus on solvent selection, a task that is particularly difficult to model theoretically and therefore ripe for machine learning applications. We showcase benchmarking for regression algorithms, transfer-learning approaches, feature engineering, and active learning, with important applications towards solvent replacement and sustainable manufacturing.

Global optimization of graph acquisition functions for neural architecture search

Graph Bayesian optimization (BO) has shown potential as a powerful and data-efficient tool for neural architecture search (NAS). Most existing graph BO works focus on developing graph surrogates models, i.e., metrics of networks and/or different kernels to quantify the similarity between networks. However, the acquisition optimization, as a discrete optimization task over graph structures, is not well studied due to the complexity of formulating the graph search space and acquisition functions. This paper presents explicit optimization formulations for graph input space including properties such as reachability and shortest paths, which are used later to formulate graph kernels and the acquisition function. We theoretically prove that the proposed encoding is an equivalent representation of the graph space and provide restrictions for the NAS domain with either node or edge labels. Numerical results over several NAS benchmarks show that our method efficiently finds the optimal architecture for most cases, highlighting its efficacy.

Global Optimization of Gaussian Process Acquisition Functions Using a Piecewise-Linear Kernel Approximation

Bayesian optimization relies on iteratively constructing and optimizing an acquisition function. The latter turns out to be a challenging, non-convex optimization problem itself. Despite the relative importance of this step, most algorithms employ sampling- or gradient-based methods, which do not provably converge to global optima. This work investigates mixed-integer programming (MIP) as a paradigm for \textit{global} acquisition function optimization. Specifically, our Piecewise-linear Kernel Mixed Integer Quadratic Programming (PK-MIQP) formulation introduces a piecewise-linear approximation for Gaussian process kernels and admits a corresponding MIQP representation for acquisition functions. We analyze the theoretical regret bounds of the proposed approximation, and empirically demonstrate the framework on synthetic functions, constrained benchmarks, and a hyperparameter tuning task.

Verifying message-passing neural networks via topology-based bounds tightening

Since graph neural networks (GNNs) are often vulnerable to attack, we need to know when we can trust them. We develop a computationally effective approach towards providing robust certificates for message-passing neural networks (MPNNs) using a Rectified Linear Unit (ReLU) activation function. Because our work builds on mixed-integer optimization, it encodes a wide variety of subproblems, for example it admits (i) both adding and removing edges, (ii) both global and local budgets, and (iii) both topological perturbations and feature modifications. Our key technology, topology-based bounds tightening, uses graph structure to tighten bounds. We also experiment with aggressive bounds tightening to dynamically change the optimization constraints by tightening variable bounds. To demonstrate the effectiveness of these strategies, we implement an extension to the open-source branch-and-cut solver SCIP. We test on both node and graph classification problems and consider topological attacks that both add and remove edges.

Practical Path-based Bayesian Optimization

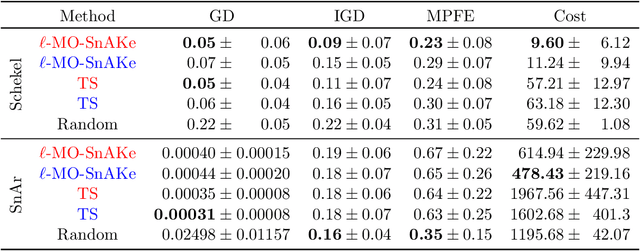
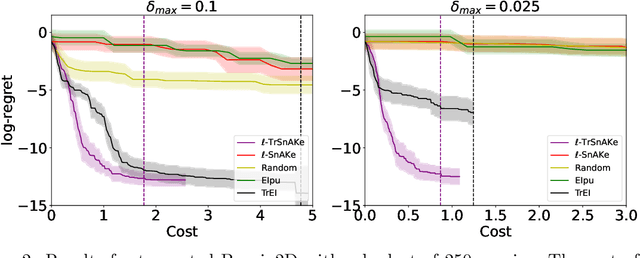
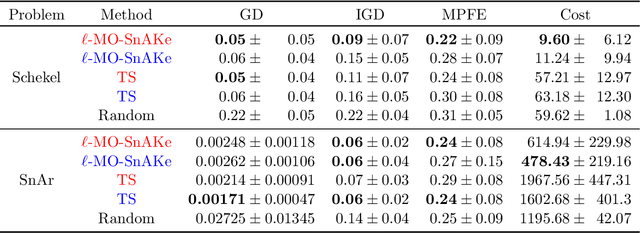
There has been a surge in interest in data-driven experimental design with applications to chemical engineering and drug manufacturing. Bayesian optimization (BO) has proven to be adaptable to such cases, since we can model the reactions of interest as expensive black-box functions. Sometimes, the cost of this black-box functions can be separated into two parts: (a) the cost of the experiment itself, and (b) the cost of changing the input parameters. In this short paper, we extend the SnAKe algorithm to deal with both types of costs simultaneously. We further propose extensions to the case of a maximum allowable input change, as well as to the multi-objective setting.

Edge-assisted U-Shaped Split Federated Learning with Privacy-preserving for Internet of Things

In the realm of the Internet of Things (IoT), deploying deep learning models to process data generated or collected by IoT devices is a critical challenge. However, direct data transmission can cause network congestion and inefficient execution, given that IoT devices typically lack computation and communication capabilities. Centralized data processing in data centers is also no longer feasible due to concerns over data privacy and security. To address these challenges, we present an innovative Edge-assisted U-Shaped Split Federated Learning (EUSFL) framework, which harnesses the high-performance capabilities of edge servers to assist IoT devices in model training and optimization process. In this framework, we leverage Federated Learning (FL) to enable data holders to collaboratively train models without sharing their data, thereby enhancing data privacy protection by transmitting only model parameters. Additionally, inspired by Split Learning (SL), we split the neural network into three parts using U-shaped splitting for local training on IoT devices. By exploiting the greater computation capability of edge servers, our framework effectively reduces overall training time and allows IoT devices with varying capabilities to perform training tasks efficiently. Furthermore, we proposed a novel noise mechanism called LabelDP to ensure that data features and labels can securely resist reconstruction attacks, eliminating the risk of privacy leakage. Our theoretical analysis and experimental results demonstrate that EUSFL can be integrated with various aggregation algorithms, maintaining good performance across different computing capabilities of IoT devices, and significantly reducing training time and local computation overhead.

SnAKe: Bayesian Optimization with Pathwise Exploration

Bayesian Optimization is a very effective tool for optimizing expensive black-box functions. Inspired by applications developing and characterizing reaction chemistry using droplet microfluidic reactors, we consider a novel setting where the expense of evaluating the function can increase significantly when making large input changes between iterations. We further assume we are working asynchronously, meaning we have to decide on new queries before we finish evaluating previous experiments. This paper investigates the problem and introduces 'Sequential Bayesian Optimization via Adaptive Connecting Samples' (SnAKe), which provides a solution by considering future queries and preemptively building optimization paths that minimize input costs. We investigate some convergence properties and empirically show that the algorithm is able to achieve regret similar to classical Bayesian Optimization algorithms in both the synchronous and asynchronous settings, while reducing the input costs significantly.

Efficient Curvature Estimation for Oriented Point Clouds

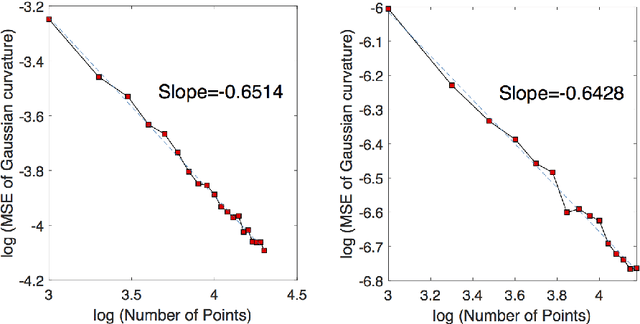
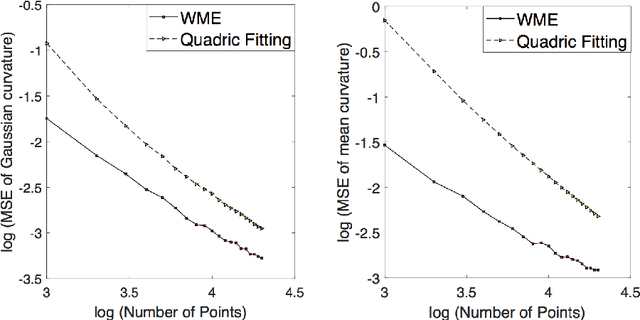
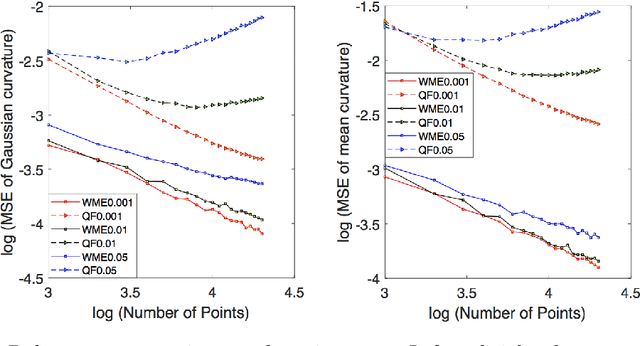
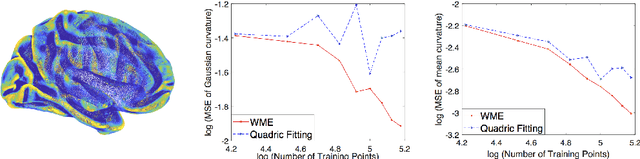
There is an immense literature focused on estimating the curvature of an unknown surface from point cloud dataset. Most existing algorithms estimate the curvature indirectly, that is, to estimate the surface locally by some basis functions and then calculate the curvature of such surface as an estimate of the curvature. Recently several methods have been proposed to estimate the curvature directly. However, these algorithms lack of theoretical guarantee on estimation error on small to moderate datasets. In this paper, we propose a direct and efficient method to estimate the curvature for oriented point cloud data without any surface approximation. In fact, we estimate the Weingarten map using a least square method, so that Gaussian curvature, mean curvature and principal curvatures can be obtained automatically from the Weingarten map. We show the convergence rate of our Weingarten Map Estimation (WME) algorithm is $n^{-2/3}$ both theoretically and numerically. Finally, we apply our method to point cloud simplification and surface reconstruction.