LDA-MIG Detectors for Maritime Targets in Nonhomogeneous Sea Clutter

This paper deals with the problem of detecting maritime targets embedded in nonhomogeneous sea clutter, where limited number of secondary data is available due to the heterogeneity of sea clutter. A class of linear discriminant analysis (LDA)-based matrix information geometry (MIG) detectors is proposed in the supervised scenario. As customary, Hermitian positive-definite (HPD) matrices are used to model the observational sample data, and the clutter covariance matrix of received dataset is estimated as geometric mean of the secondary HPD matrices. Given a set of training HPD matrices with class labels, that are elements of a higher-dimensional HPD matrix manifold, the LDA manifold projection learns a mapping from the higher-dimensional HPD matrix manifold to a lower-dimensional one subject to maximum discrimination. In the current study, the LDA manifold projection, with the cost function maximizing between-class distance while minimizing within-class distance, is formulated as an optimization problem in the Stiefel manifold. Four robust LDA-MIG detectors corresponding to different geometric measures are proposed. Numerical results based on both simulated radar clutter with interferences and real IPIX radar data show the advantage of the proposed LDA-MIG detectors against their counterparts without using LDA as well as the state-of-art maritime target detection methods in nonhomogeneous sea clutter.

AWCD: An Efficient Point Cloud Processing Approach via Wasserstein Curvature

In this paper, we introduce the adaptive Wasserstein curvature denoising (AWCD), an original processing approach for point cloud data. By collecting curvatures information from Wasserstein distance, AWCD consider more precise structures of data and preserves stability and effectiveness even for data with noise in high density. This paper contains some theoretical analysis about the Wasserstein curvature and the complete algorithm of AWCD. In addition, we design digital experiments to show the denoising effect of AWCD. According to comparison results, we present the advantages of AWCD against traditional algorithms.

Efficient Curvature Estimation for Oriented Point Clouds

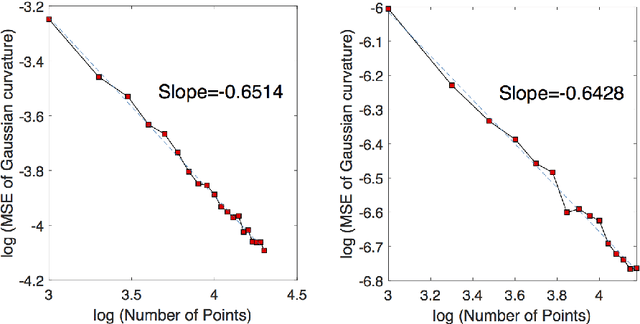
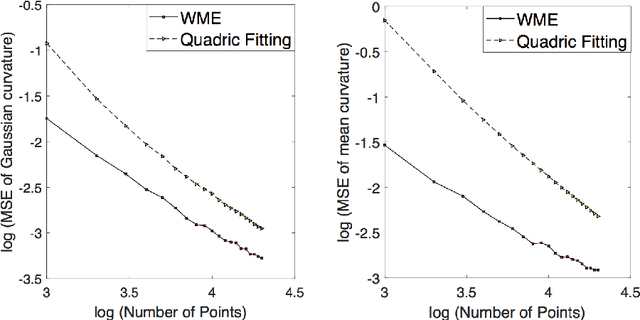
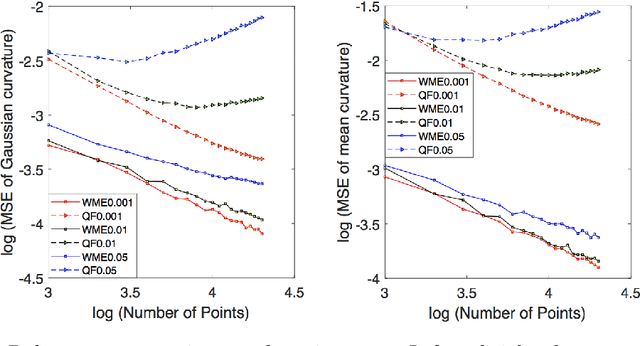
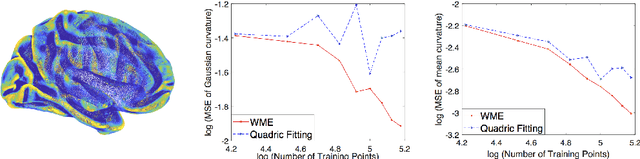
There is an immense literature focused on estimating the curvature of an unknown surface from point cloud dataset. Most existing algorithms estimate the curvature indirectly, that is, to estimate the surface locally by some basis functions and then calculate the curvature of such surface as an estimate of the curvature. Recently several methods have been proposed to estimate the curvature directly. However, these algorithms lack of theoretical guarantee on estimation error on small to moderate datasets. In this paper, we propose a direct and efficient method to estimate the curvature for oriented point cloud data without any surface approximation. In fact, we estimate the Weingarten map using a least square method, so that Gaussian curvature, mean curvature and principal curvatures can be obtained automatically from the Weingarten map. We show the convergence rate of our Weingarten Map Estimation (WME) algorithm is $n^{-2/3}$ both theoretically and numerically. Finally, we apply our method to point cloud simplification and surface reconstruction.