Data-Efficient CLIP-Powered Dual-Branch Networks for Source-Free Unsupervised Domain Adaptation

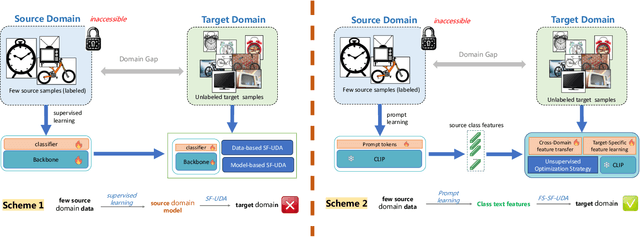
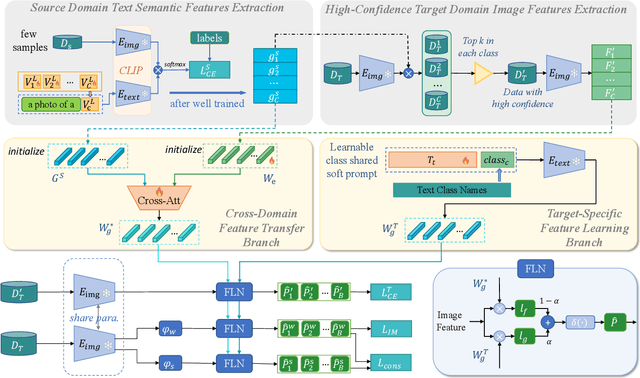
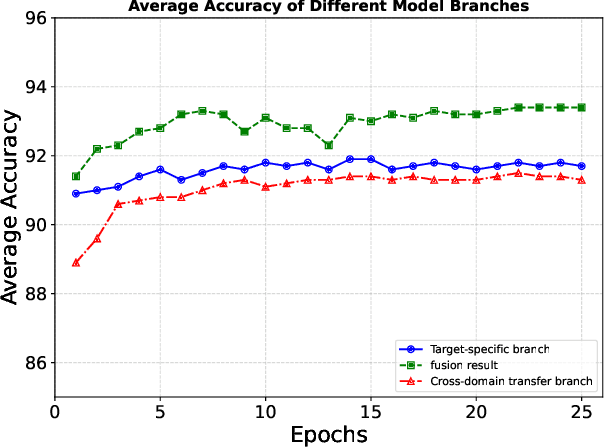
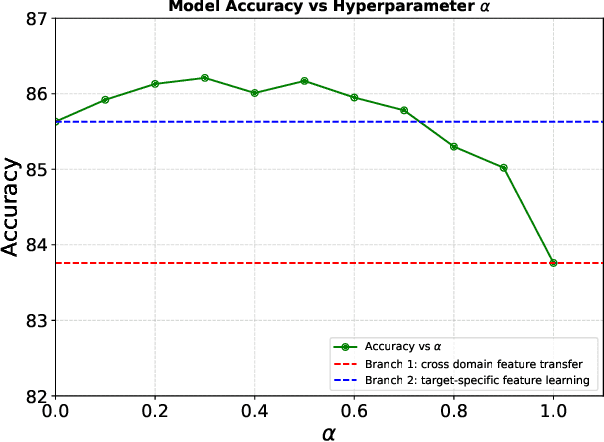
Source-Free Unsupervised Domain Adaptation (SF-UDA) aims to transfer a model's performance from a labeled source domain to an unlabeled target domain without direct access to source samples, addressing data privacy issues. However, most existing SF-UDA approaches assume the availability of abundant source domain samples, which is often impractical due to the high cost of data annotation. In this paper, we explore a more challenging scenario where direct access to source domain samples is restricted, and the source domain contains only a few samples. To tackle the dual challenges of limited source data and privacy concerns, we introduce a data-efficient, CLIP-powered dual-branch network (CDBN in short). We design a cross-modal dual-branch network that integrates source domain class semantics into the unsupervised fine-tuning of the target domain. It preserves the class information from the source domain while enhancing the model's generalization to the target domain. Additionally, we propose an unsupervised optimization strategy driven by accurate classification and diversity, which aims to retain the classification capability learned from the source domain while producing more confident and diverse predictions in the target domain. Extensive experiments across 31 transfer tasks on 7 public datasets demonstrate that our approach achieves state-of-the-art performance compared to existing methods.

Tropical Expressivity of Neural Networks

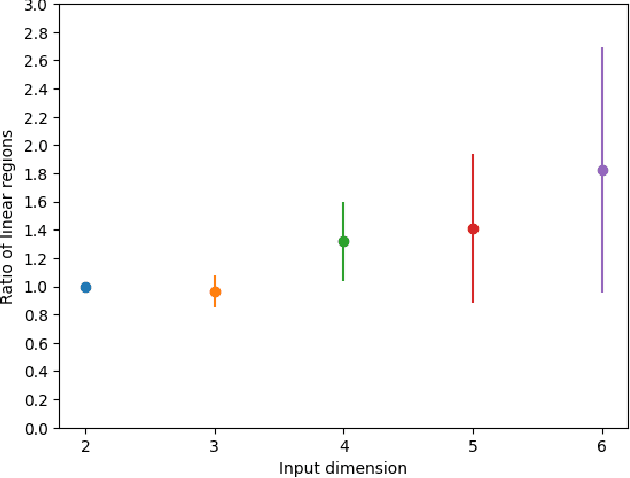
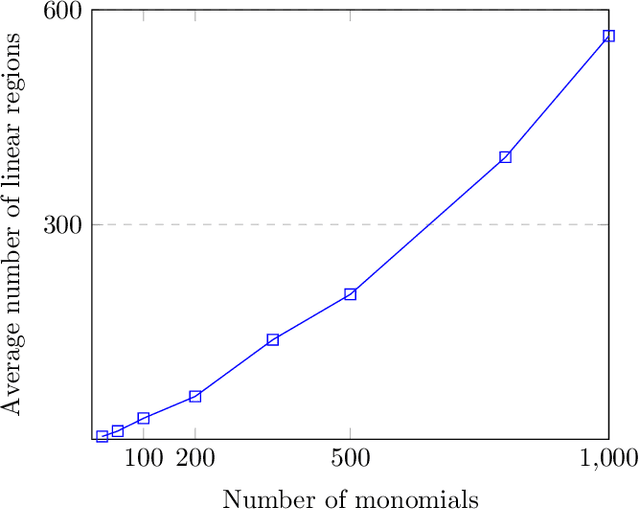
We propose an algebraic geometric framework to study the expressivity of linear activation neural networks. A particular quantity that has been actively studied in the field of deep learning is the number of linear regions, which gives an estimate of the information capacity of the architecture. To study and evaluate information capacity and expressivity, we work in the setting of tropical geometry -- a combinatorial and polyhedral variant of algebraic geometry -- where there are known connections between tropical rational maps and feedforward neural networks. Our work builds on and expands this connection to capitalize on the rich theory of tropical geometry to characterize and study various architectural aspects of neural networks. Our contributions are threefold: we provide a novel tropical geometric approach to selecting sampling domains among linear regions; an algebraic result allowing for a guided restriction of the sampling domain for network architectures with symmetries; and an open source library to analyze neural networks as tropical Puiseux rational maps. We provide a comprehensive set of proof-of-concept numerical experiments demonstrating the breadth of neural network architectures to which tropical geometric theory can be applied to reveal insights on expressivity characteristics of a network. Our work provides the foundations for the adaptation of both theory and existing software from computational tropical geometry and symbolic computation to deep learning.

$k$-Means Clustering for Persistent Homology

Persistent homology is a fundamental methodology from topological data analysis that summarizes the lifetimes of topological features within a dataset as a persistence diagram; it has recently gained much popularity from its myriad successful applications to many domains. However, a significant challenge to its widespread implementation, especially in statistical methodology and machine learning algorithms, is the format of the persistence diagram as a multiset of half-open intervals. In this paper, we comprehensively study $k$-means clustering where the input is various embeddings of persistence diagrams, as well as persistence diagrams themselves and their generalizations as persistence measures. We show that the clustering performance directly on persistence diagrams and measures far outperform their vectorized representations, despite their more complex representations. Moreover, we prove convergence of the algorithm on persistence diagram space and establish theoretical properties of the solution to the optimization problem in the Karush--Kuhn--Tucker framework.

Approximating Persistent Homology for Large Datasets

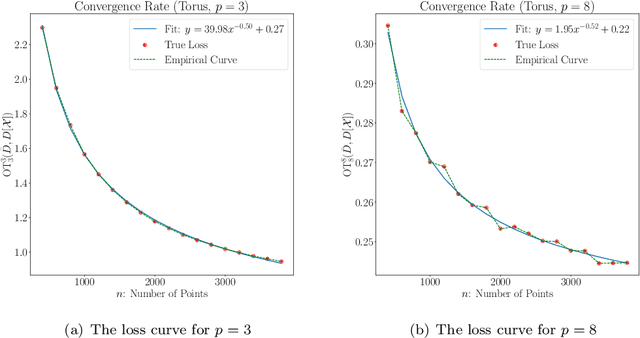
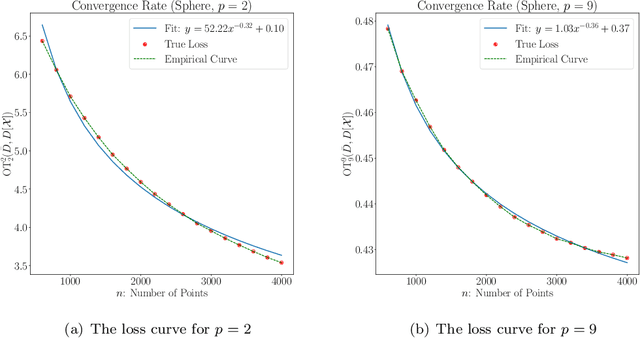
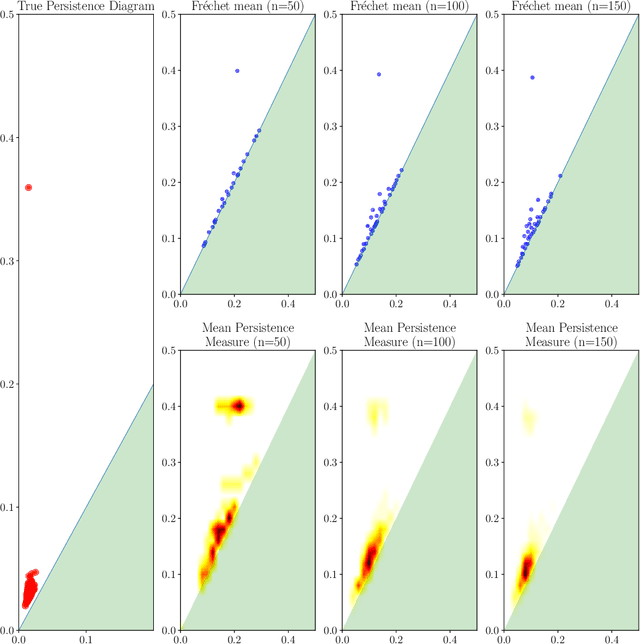
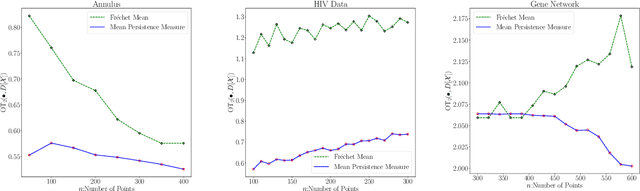
Persistent homology is an important methodology from topological data analysis which adapts theory from algebraic topology to data settings and has been successfully implemented in many applications. It produces a statistical summary in the form of a persistence diagram, which captures the shape and size of the data. Despite its widespread use, persistent homology is simply impossible to implement when a dataset is very large. In this paper we address the problem of finding a representative persistence diagram for prohibitively large datasets. We adapt the classical statistical method of bootstrapping, namely, drawing and studying smaller multiple subsamples from the large dataset. We show that the mean of the persistence diagrams of subsamples -- taken as a mean persistence measure computed from the subsamples -- is a valid approximation of the true persistent homology of the larger dataset. We give the rate of convergence of the mean persistence diagram to the true persistence diagram in terms of the number of subsamples and size of each subsample. Given the complex algebraic and geometric nature of persistent homology, we adapt the convexity and stability properties in the space of persistence diagrams together with random set theory to achieve our theoretical results for the general setting of point cloud data. We demonstrate our approach on simulated and real data, including an application of shape clustering on complex large-scale point cloud data.

Topological Data Analysis of Database Representations for Information Retrieval

Appropriately representing elements in a database so that queries may be accurately matched is a central task in information retrieval. This recently has been achieved by embedding the graphical structure of the database into a manifold so that the hierarchy is preserved. Persistent homology provides a rigorous characterization for the database topology in terms of both its hierarchy and connectivity structure. We compute persistent homology on a variety of datasets and show that some commonly used embeddings fail to preserve the connectivity. Moreover, we show that embeddings which successfully retain the database topology coincide in persistent homology. We introduce the dilation-invariant bottleneck distance to capture this effect, which addresses metric distortion on manifolds. We use it to show that distances between topology-preserving embeddings of databases are small.

Efficient Curvature Estimation for Oriented Point Clouds

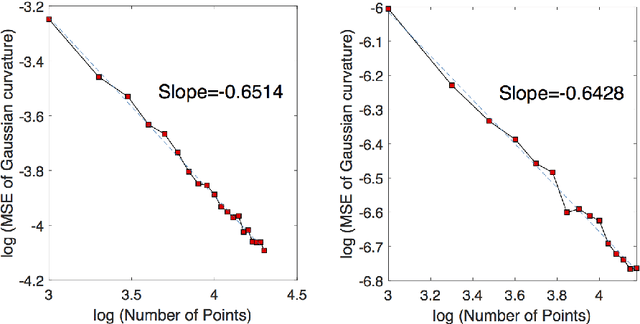
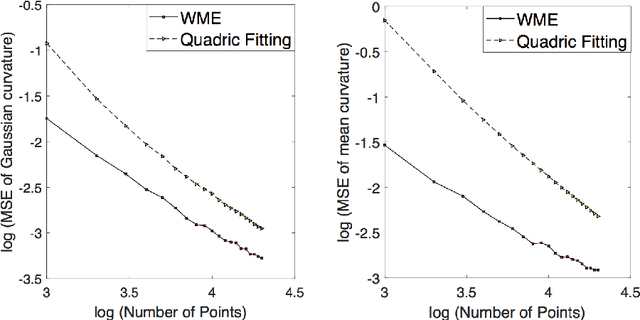
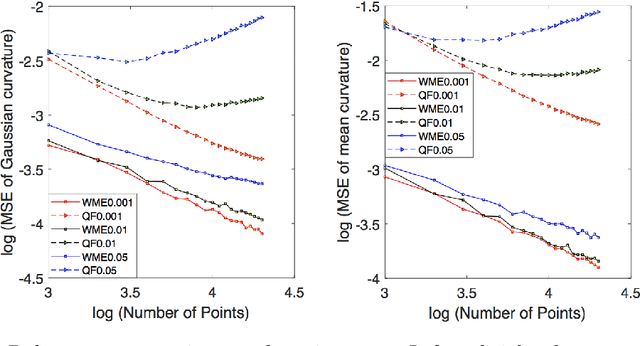
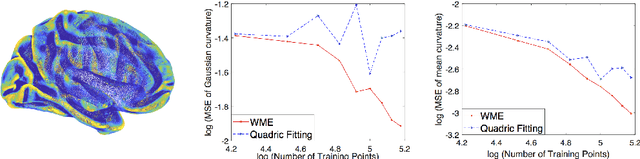
There is an immense literature focused on estimating the curvature of an unknown surface from point cloud dataset. Most existing algorithms estimate the curvature indirectly, that is, to estimate the surface locally by some basis functions and then calculate the curvature of such surface as an estimate of the curvature. Recently several methods have been proposed to estimate the curvature directly. However, these algorithms lack of theoretical guarantee on estimation error on small to moderate datasets. In this paper, we propose a direct and efficient method to estimate the curvature for oriented point cloud data without any surface approximation. In fact, we estimate the Weingarten map using a least square method, so that Gaussian curvature, mean curvature and principal curvatures can be obtained automatically from the Weingarten map. We show the convergence rate of our Weingarten Map Estimation (WME) algorithm is $n^{-2/3}$ both theoretically and numerically. Finally, we apply our method to point cloud simplification and surface reconstruction.