LDA-MIG Detectors for Maritime Targets in Nonhomogeneous Sea Clutter

This paper deals with the problem of detecting maritime targets embedded in nonhomogeneous sea clutter, where limited number of secondary data is available due to the heterogeneity of sea clutter. A class of linear discriminant analysis (LDA)-based matrix information geometry (MIG) detectors is proposed in the supervised scenario. As customary, Hermitian positive-definite (HPD) matrices are used to model the observational sample data, and the clutter covariance matrix of received dataset is estimated as geometric mean of the secondary HPD matrices. Given a set of training HPD matrices with class labels, that are elements of a higher-dimensional HPD matrix manifold, the LDA manifold projection learns a mapping from the higher-dimensional HPD matrix manifold to a lower-dimensional one subject to maximum discrimination. In the current study, the LDA manifold projection, with the cost function maximizing between-class distance while minimizing within-class distance, is formulated as an optimization problem in the Stiefel manifold. Four robust LDA-MIG detectors corresponding to different geometric measures are proposed. Numerical results based on both simulated radar clutter with interferences and real IPIX radar data show the advantage of the proposed LDA-MIG detectors against their counterparts without using LDA as well as the state-of-art maritime target detection methods in nonhomogeneous sea clutter.

Unsupervised Learning Discriminative MIG Detectors in Nonhomogeneous Clutter

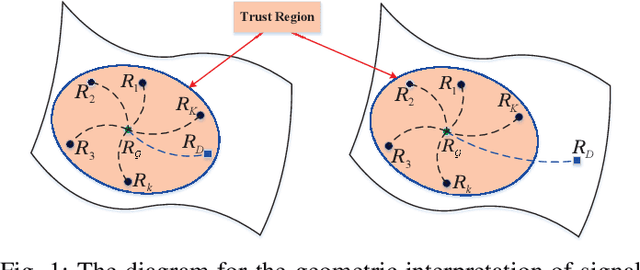
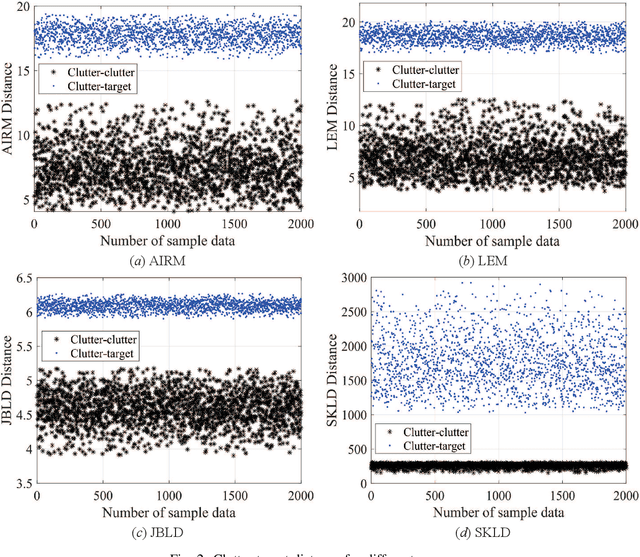
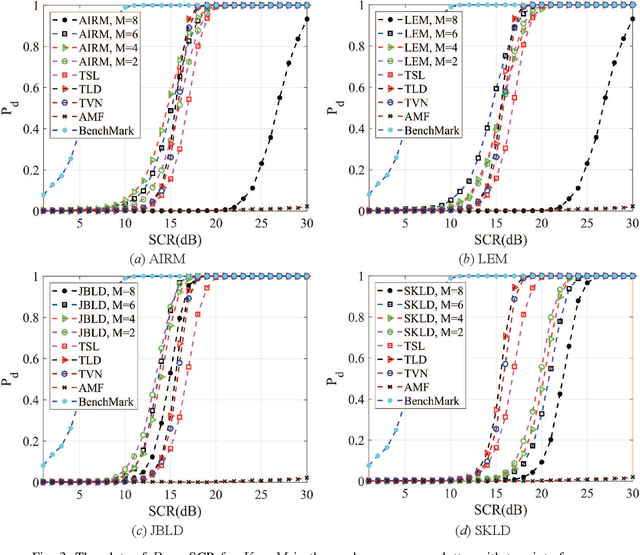
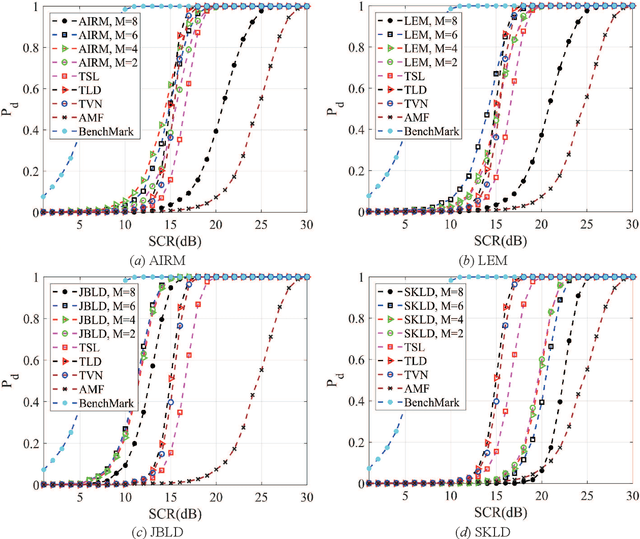
Principal component analysis (PCA) is a common used pattern analysis method that maps high-dimensional data into a lower-dimensional space maximizing the data variance, that results in the promotion of separability of data. Inspired by the principle of PCA, a novel type of learning discriminative matrix information geometry (MIG) detectors in the unsupervised scenario are developed, and applied to signal detection in nonhomogeneous environments. Hermitian positive-definite (HPD) matrices can be used to model the sample data, while the clutter covariance matrix is estimated by the geometric mean of a set of secondary HPD matrices. We define a projection that maps the HPD matrices in a high-dimensional manifold to a low-dimensional and more discriminative one to increase the degree of separation of HPD matrices by maximizing the data variance. Learning a mapping can be formulated as a two-step mini-max optimization problem in Riemannian manifolds, which can be solved by the Riemannian gradient descent algorithm. Three discriminative MIG detectors are illustrated with respect to different geometric measures, i.e., the Log-Euclidean metric, the Jensen--Bregman LogDet divergence and the symmetrized Kullback--Leibler divergence. Simulation results show that performance improvements of the novel MIG detectors can be achieved compared with the conventional detectors and their state-of-the-art counterparts within nonhomogeneous environments.

MIG Median Detectors with Manifold Filter

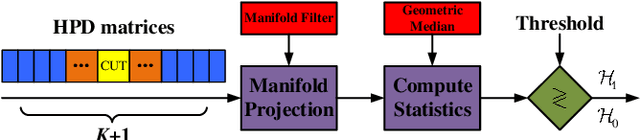
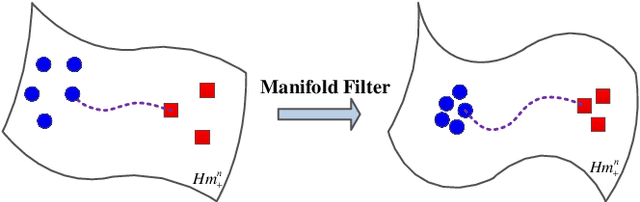
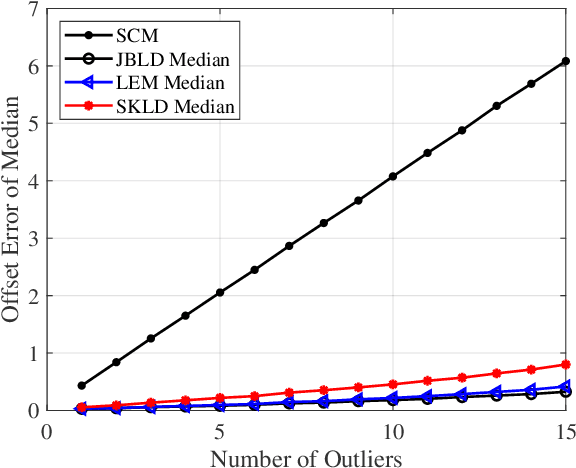
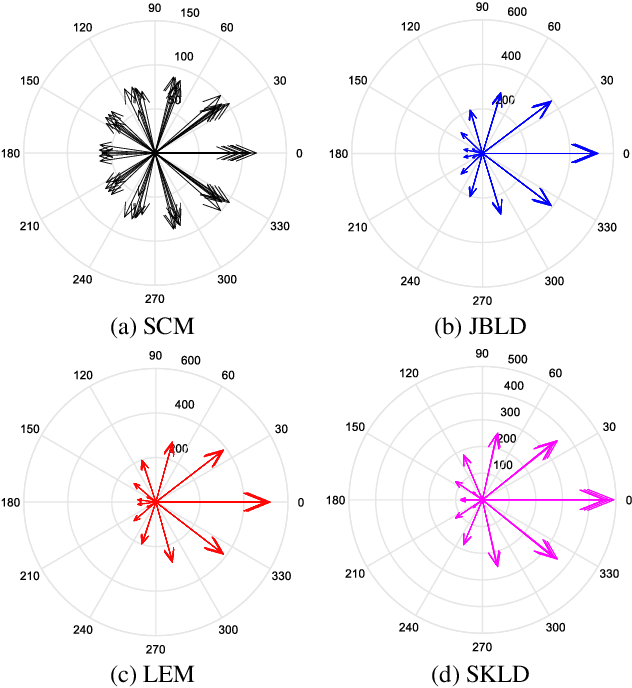
In this paper, we propose a class of median-based matrix information geometry (MIG) detectors with a manifold filter and apply them to signal detection in nonhomogeneous environments. As customary, the sample data is assumed to be modeled as Hermitian positive-definite (HPD) matrices, and the geometric median of a set of HPD matrices is interpreted as an estimate of the clutter covariance matrix (CCM). Then, the problem of signal detection can be reformulated as discriminating two points on the manifold of HPD matrices, one of which is the HPD matrix in the cell under test while the other represents the CCM. By manifold filter, we map a set of HPD matrices to another set of HPD matrices by weighting them, that consequently improves the discriminative power by reducing the intra-class distances while increasing the inter-class distances. Three MIG median detectors are designed by resorting to three geometric measures on the matrix manifold, and the corresponding geometric medians are shown to be robust to outliers. Numerical simulations show the advantage of the proposed MIG median detectors in comparison with their state-of-the-art counterparts as well as the conventional detectors in nonhomogeneous environments.

Target Detection within Nonhomogeneous Clutter via Total Bregman Divergence-Based Matrix Information Geometry Detectors

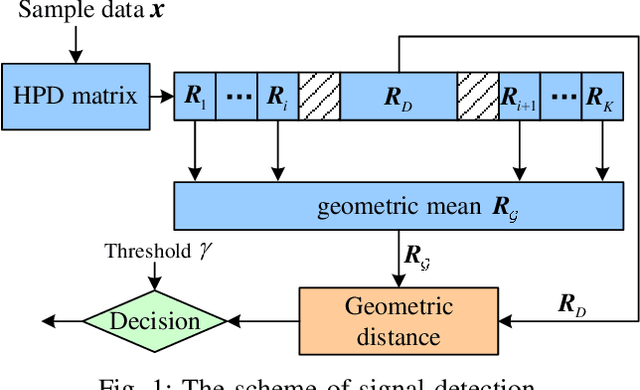
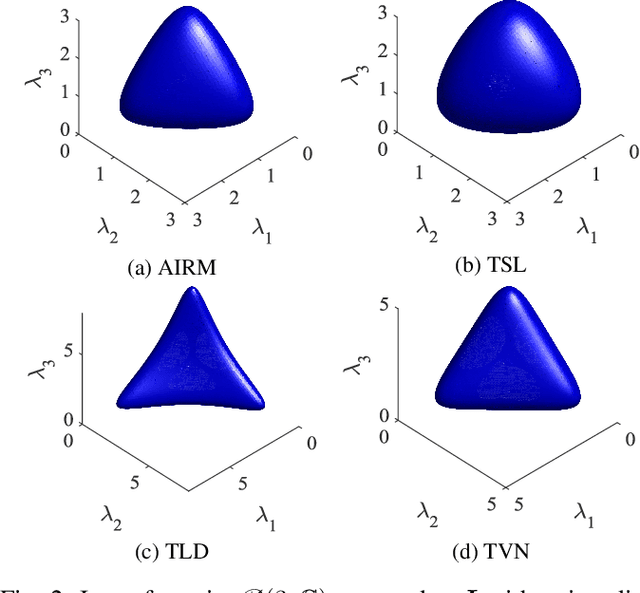
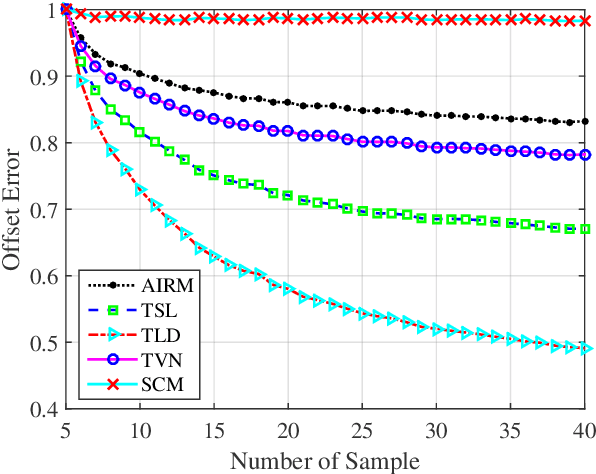
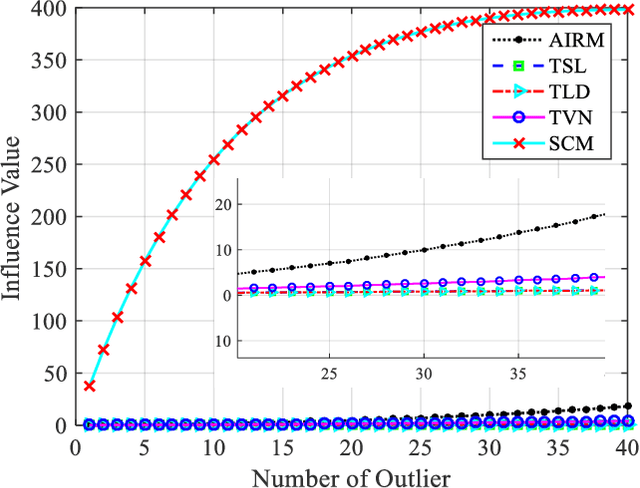
Information divergences are commonly used to measure the dissimilarity of two elements on a statistical manifold. Differentiable manifolds endowed with different divergences may possess different geometric properties, which can result in totally different performances in many practical applications. In this paper, we propose a total Bregman divergence-based matrix information geometry (TBD-MIG) detector and apply it to detect targets emerged into nonhomogeneous clutter. In particular, each sample data is assumed to be modeled as a Hermitian positive-definite (HPD) matrix and the clutter covariance matrix is estimated by the TBD mean of a set of secondary HPD matrices. We then reformulate the problem of signal detection as discriminating two points on the HPD matrix manifold. Three TBD-MIG detectors, referred to as the total square loss, the total log-determinant and the total von Neumann MIG detectors, are proposed, and they can achieve great performances due to their power of discrimination and robustness to interferences. Simulations show the advantage of the proposed TBD-MIG detectors in comparison with the geometric detector using an affine invariant Riemannian metric as well as the adaptive matched filter in nonhomogeneous clutter.