PR-CapsNet: Pseudo-Riemannian Capsule Network with Adaptive Curvature Routing for Graph Learning

Capsule Networks (CapsNets) show exceptional graph representation capacity via dynamic routing and vectorized hierarchical representations, but they model the complex geometries of real\-world graphs poorly by fixed\-curvature space due to the inherent geodesical disconnectedness issues, leading to suboptimal performance. Recent works find that non\-Euclidean pseudo\-Riemannian manifolds provide specific inductive biases for embedding graph data, but how to leverage them to improve CapsNets is still underexplored. Here, we extend the Euclidean capsule routing into geodesically disconnected pseudo\-Riemannian manifolds and derive a Pseudo\-Riemannian Capsule Network (PR\-CapsNet), which models data in pseudo\-Riemannian manifolds of adaptive curvature, for graph representation learning. Specifically, PR\-CapsNet enhances the CapsNet with Adaptive Pseudo\-Riemannian Tangent Space Routing by utilizing pseudo\-Riemannian geometry. Unlike single\-curvature or subspace\-partitioning methods, PR\-CapsNet concurrently models hierarchical and cluster or cyclic graph structures via its versatile pseudo\-Riemannian metric. It first deploys Pseudo\-Riemannian Tangent Space Routing to decompose capsule states into spherical\-temporal and Euclidean\-spatial subspaces with diffeomorphic transformations. Then, an Adaptive Curvature Routing is developed to adaptively fuse features from different curvature spaces for complex graphs via a learnable curvature tensor with geometric attention from local manifold properties. Finally, a geometric properties\-preserved Pseudo\-Riemannian Capsule Classifier is developed to project capsule embeddings to tangent spaces and use curvature\-weighted softmax for classification. Extensive experiments on node and graph classification benchmarks show PR\-CapsNet outperforms SOTA models, validating PR\-CapsNet's strong representation power for complex graph structures.

Mask-RadarNet: Enhancing Transformer With Spatial-Temporal Semantic Context for Radar Object Detection in Autonomous Driving

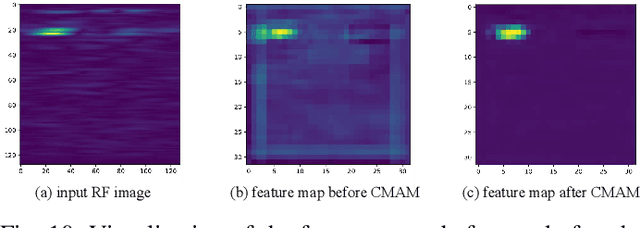
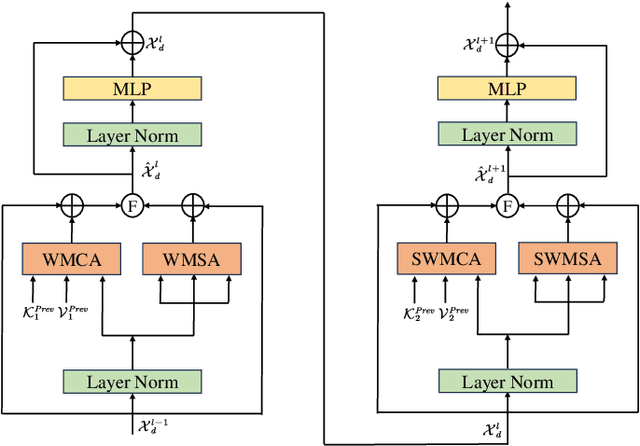
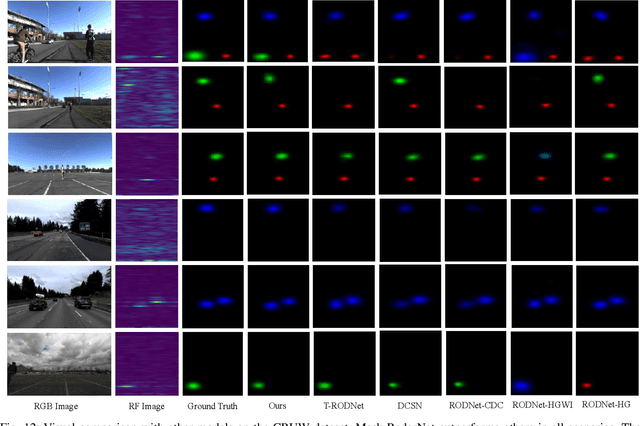
As a cost-effective and robust technology, automotive radar has seen steady improvement during the last years, making it an appealing complement to commonly used sensors like camera and LiDAR in autonomous driving. Radio frequency data with rich semantic information are attracting more and more attention. Most current radar-based models take radio frequency image sequences as the input. However, these models heavily rely on convolutional neural networks and leave out the spatial-temporal semantic context during the encoding stage. To solve these problems, we propose a model called Mask-RadarNet to fully utilize the hierarchical semantic features from the input radar data. Mask-RadarNet exploits the combination of interleaved convolution and attention operations to replace the traditional architecture in transformer-based models. In addition, patch shift is introduced to the Mask-RadarNet for efficient spatial-temporal feature learning. By shifting part of patches with a specific mosaic pattern in the temporal dimension, Mask-RadarNet achieves competitive performance while reducing the computational burden of the spatial-temporal modeling. In order to capture the spatial-temporal semantic contextual information, we design the class masking attention module (CMAM) in our encoder. Moreover, a lightweight auxiliary decoder is added to our model to aggregate prior maps generated from the CMAM. Experiments on the CRUW dataset demonstrate the superiority of the proposed method to some state-of-the-art radar-based object detection algorithms. With relatively lower computational complexity and fewer parameters, the proposed Mask-RadarNet achieves higher recognition accuracy for object detection in autonomous driving.

LDA-MIG Detectors for Maritime Targets in Nonhomogeneous Sea Clutter

This paper deals with the problem of detecting maritime targets embedded in nonhomogeneous sea clutter, where limited number of secondary data is available due to the heterogeneity of sea clutter. A class of linear discriminant analysis (LDA)-based matrix information geometry (MIG) detectors is proposed in the supervised scenario. As customary, Hermitian positive-definite (HPD) matrices are used to model the observational sample data, and the clutter covariance matrix of received dataset is estimated as geometric mean of the secondary HPD matrices. Given a set of training HPD matrices with class labels, that are elements of a higher-dimensional HPD matrix manifold, the LDA manifold projection learns a mapping from the higher-dimensional HPD matrix manifold to a lower-dimensional one subject to maximum discrimination. In the current study, the LDA manifold projection, with the cost function maximizing between-class distance while minimizing within-class distance, is formulated as an optimization problem in the Stiefel manifold. Four robust LDA-MIG detectors corresponding to different geometric measures are proposed. Numerical results based on both simulated radar clutter with interferences and real IPIX radar data show the advantage of the proposed LDA-MIG detectors against their counterparts without using LDA as well as the state-of-art maritime target detection methods in nonhomogeneous sea clutter.