LDA-MIG Detectors for Maritime Targets in Nonhomogeneous Sea Clutter

This paper deals with the problem of detecting maritime targets embedded in nonhomogeneous sea clutter, where limited number of secondary data is available due to the heterogeneity of sea clutter. A class of linear discriminant analysis (LDA)-based matrix information geometry (MIG) detectors is proposed in the supervised scenario. As customary, Hermitian positive-definite (HPD) matrices are used to model the observational sample data, and the clutter covariance matrix of received dataset is estimated as geometric mean of the secondary HPD matrices. Given a set of training HPD matrices with class labels, that are elements of a higher-dimensional HPD matrix manifold, the LDA manifold projection learns a mapping from the higher-dimensional HPD matrix manifold to a lower-dimensional one subject to maximum discrimination. In the current study, the LDA manifold projection, with the cost function maximizing between-class distance while minimizing within-class distance, is formulated as an optimization problem in the Stiefel manifold. Four robust LDA-MIG detectors corresponding to different geometric measures are proposed. Numerical results based on both simulated radar clutter with interferences and real IPIX radar data show the advantage of the proposed LDA-MIG detectors against their counterparts without using LDA as well as the state-of-art maritime target detection methods in nonhomogeneous sea clutter.

Structural Constraint Integration in Generative Model for Discovery of Quantum Material Candidates

Billions of organic molecules are known, but only a tiny fraction of the functional inorganic materials have been discovered, a particularly relevant problem to the community searching for new quantum materials. Recent advancements in machine-learning-based generative models, particularly diffusion models, show great promise for generating new, stable materials. However, integrating geometric patterns into materials generation remains a challenge. Here, we introduce Structural Constraint Integration in the GENerative model (SCIGEN). Our approach can modify any trained generative diffusion model by strategic masking of the denoised structure with a diffused constrained structure prior to each diffusion step to steer the generation toward constrained outputs. Furthermore, we mathematically prove that SCIGEN effectively performs conditional sampling from the original distribution, which is crucial for generating stable constrained materials. We generate eight million compounds using Archimedean lattices as prototype constraints, with over 10% surviving a multi-staged stability pre-screening. High-throughput density functional theory (DFT) on 26,000 survived compounds shows that over 50% passed structural optimization at the DFT level. Since the properties of quantum materials are closely related to geometric patterns, our results indicate that SCIGEN provides a general framework for generating quantum materials candidates.

Low Rank Properties for Estimating Microphones Start Time and Sources Emission Time

Uncertainty in timing information pertaining to the start time of microphone recordings and sources' emission time pose significant challenges in various applications, such as joint microphones and sources localization. Traditional optimization methods, which directly estimate this unknown timing information (UTIm), often fall short compared to approaches exploiting the low-rank property (LRP). LRP encompasses an additional low-rank structure, facilitating a linear constraint on UTIm to help formulate related low-rank structure information. This method allows us to attain globally optimal solutions for UTIm, given proper initialization. However, the initialization process often involves randomness, leading to suboptimal, local minimum values. This paper presents a novel, combined low-rank approximation (CLRA) method designed to mitigate the effects of this random initialization. We introduce three new LRP variants, underpinned by mathematical proof, which allow the UTIm to draw on a richer pool of low-rank structural information. Utilizing this augmented low-rank structural information from both LRP and the proposed variants, we formulate four linear constraints on the UTIm. Employing the proposed CLRA algorithm, we derive global optimal solutions for the UTIm via these four linear constraints.Experimental results highlight the superior performance of our method over existing state-of-the-art approaches, measured in terms of both the recovery number and reduced estimation errors of UTIm.

Are Microphone Signals Alone Sufficient for Joint Microphones and Sources Localization?

Joint microphones and sources localization can be achieved by using both time of arrival (TOA) and time difference of arrival (TDOA) measurements, even in scenarios where both microphones and sources are asynchronous due to unknown emission time of human voices or sources and unknown recording start time of independent microphones. However, TOA measurements require both microphone signals and the waveform of source signals while TDOA measurements can be obtained using microphone signals alone. In this letter, we explore the sufficiency of using only microphone signals for joint microphones and sources localization by presenting two mapping functions for both TOA and TDOA formulas. Our proposed mapping functions demonstrate that the transformations of TOA and TDOA formulas can be the same, indicating that microphone signals alone are sufficient for joint microphones and sources localization without knowledge of the waveform of source signals. We have validated our proposed mapping functions through both mathematical proof and experimental results.

Justices for Information Bottleneck Theory

This study comes as a timely response to mounting criticism of the information bottleneck (IB) theory, injecting fresh perspectives to rectify misconceptions and reaffirm its validity. Firstly, we introduce an auxiliary function to reinterpret the maximal coding rate reduction method as a special yet local optimal case of IB theory. Through this auxiliary function, we clarify the paradox of decreasing mutual information during the application of ReLU activation in deep learning (DL) networks. Secondly, we challenge the doubts about IB theory's applicability by demonstrating its capacity to explain the absence of a compression phase with linear activation functions in hidden layers, when viewed through the lens of the auxiliary function. Lastly, by taking a novel theoretical stance, we provide a new way to interpret the inner organizations of DL networks by using IB theory, aligning them with recent experimental evidence. Thus, this paper serves as an act of justice for IB theory, potentially reinvigorating its standing and application in DL and other fields such as communications and biomedical research.

Dual Power Spectrum Manifold and Toeplitz HPD Manifold: Enhancement and Analysis for Matrix CFAR Detection

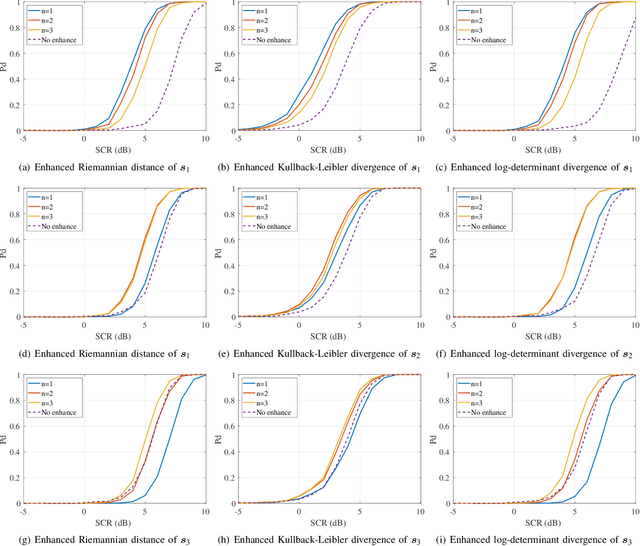
Recently, an innovative matrix CFAR detection scheme based on information geometry, also referred to as the geometric detector, has been developed speedily and exhibits distinct advantages in several practical applications. These advantages benefit from the geometry of the Toeplitz Hermitian positive definite (HPD) manifold $\mathcal{M}_{\mathcal{T}H_{++}}$, but the sophisticated geometry also results in some challenges for geometric detectors, such as the implementation of the enhanced detector to improve the SCR (signal-to-clutter ratio) and the analysis of the detection performance. To meet these challenges, this paper develops the dual power spectrum manifold $\mathcal{M}_{\text{P}}$ as the dual space of $\mathcal{M}_{\mathcal{T}H_{++}}$. For each affine invariant geometric measure on $\mathcal{M}_{\mathcal{T}H_{++}}$, we show that there exists an equivalent function named induced potential function on $\mathcal{M}_{\text{P}}$. By the induced potential function, the measurements of the dissimilarity between two matrices can be implemented on $\mathcal{M}_{\text{P}}$, and the geometric detectors can be reformulated as the form related to the power spectrum. The induced potential function leads to two contributions: 1) The enhancement of the geometric detector, which is formulated as an optimization problem concerning $\mathcal{M}_{\mathcal{T}H_{++}}$, is transformed to an equivalent and simpler optimization on $\mathcal{M}_{\text{P}}$. In the presented example of the enhancement, the closed-form solution, instead of the gradient descent method, is provided through the equivalent optimization. 2) The detection performance is analyzed based on $\mathcal{M}_{\text{P}}$, and the advantageous characteristics, which benefit the detection performance, can be deduced by analyzing the corresponding power spectrum to the maximal point of the induced potential function.

Target Detection within Nonhomogeneous Clutter via Total Bregman Divergence-Based Matrix Information Geometry Detectors

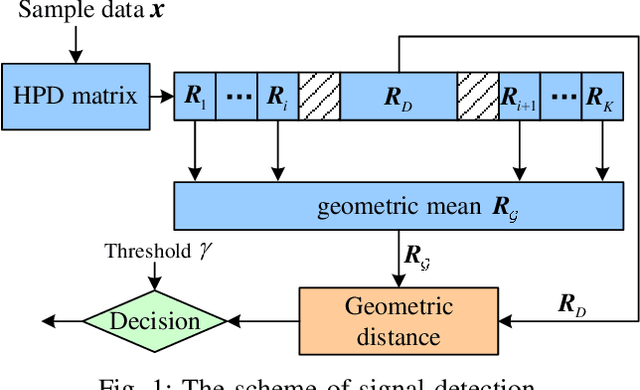
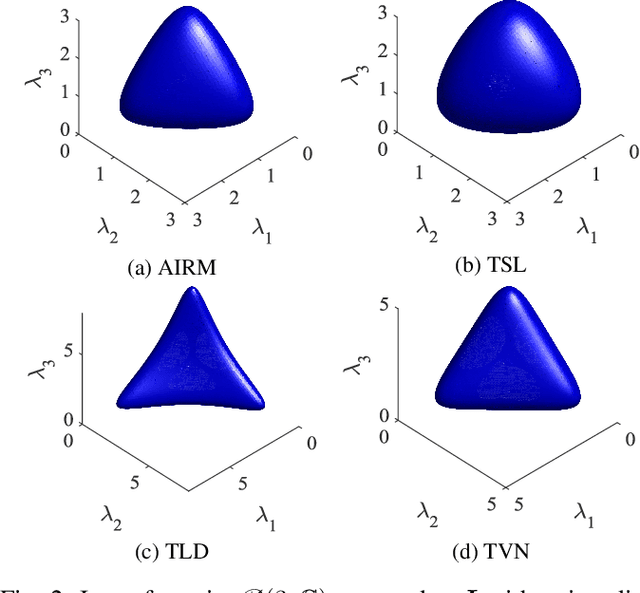
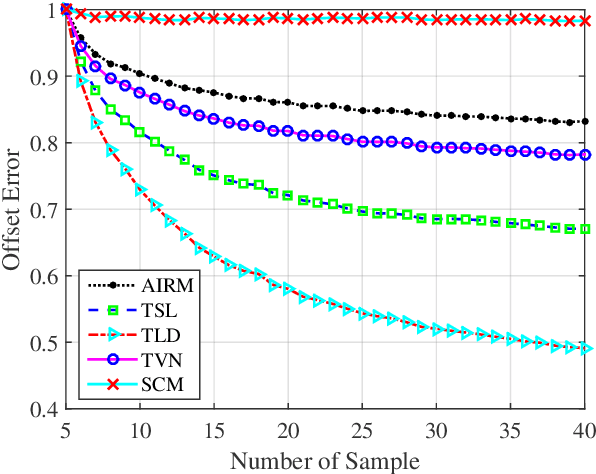
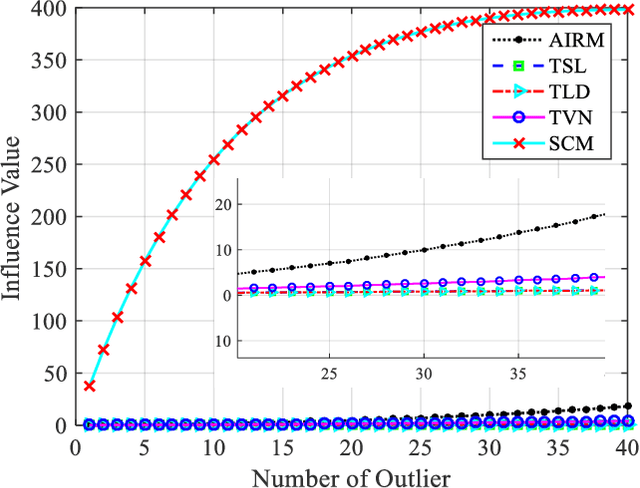
Information divergences are commonly used to measure the dissimilarity of two elements on a statistical manifold. Differentiable manifolds endowed with different divergences may possess different geometric properties, which can result in totally different performances in many practical applications. In this paper, we propose a total Bregman divergence-based matrix information geometry (TBD-MIG) detector and apply it to detect targets emerged into nonhomogeneous clutter. In particular, each sample data is assumed to be modeled as a Hermitian positive-definite (HPD) matrix and the clutter covariance matrix is estimated by the TBD mean of a set of secondary HPD matrices. We then reformulate the problem of signal detection as discriminating two points on the HPD matrix manifold. Three TBD-MIG detectors, referred to as the total square loss, the total log-determinant and the total von Neumann MIG detectors, are proposed, and they can achieve great performances due to their power of discrimination and robustness to interferences. Simulations show the advantage of the proposed TBD-MIG detectors in comparison with the geometric detector using an affine invariant Riemannian metric as well as the adaptive matched filter in nonhomogeneous clutter.