The Comparison of Riemannian Geometric Matrix-CFAR Signal Detectors

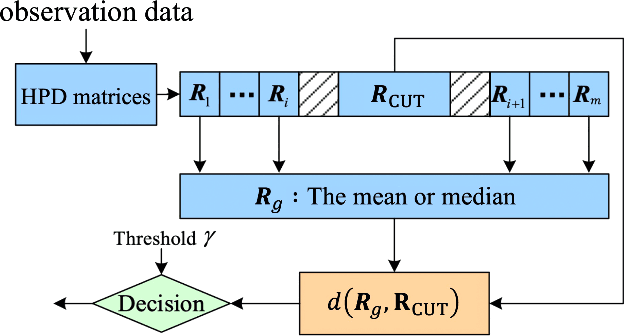
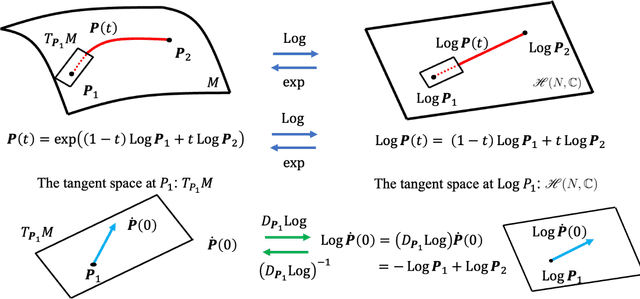
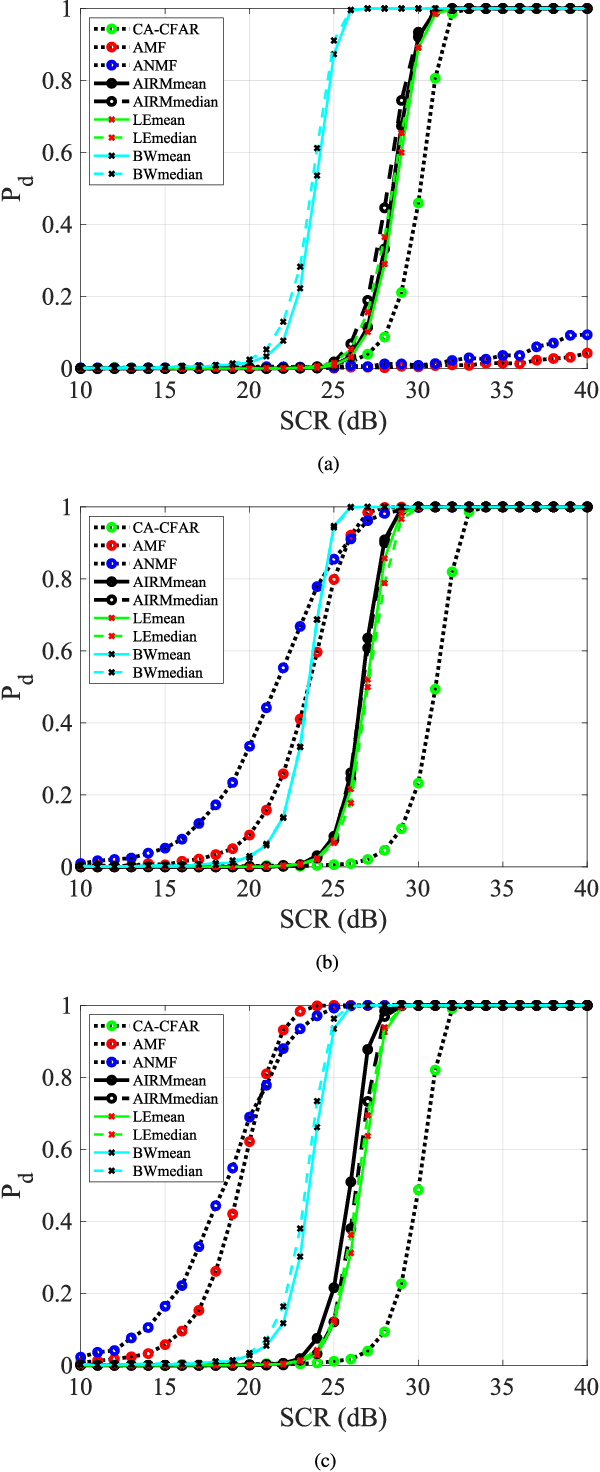
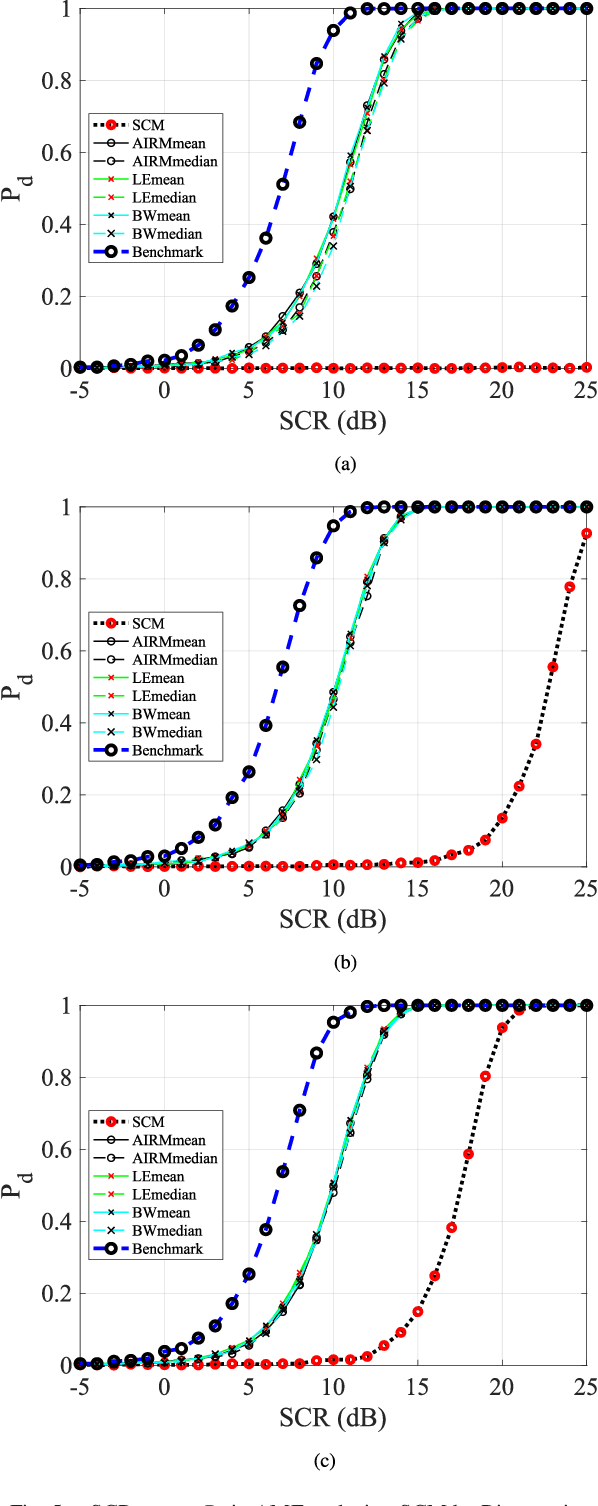
Essential characteristics of signal data can be captured by the autocovariance matrix, which, in the stationary scenarios, is Toeplitz Hermitian positive definite (HPD). In this paper, several well-known Riemannian geometric structures of HPD matrix manifolds are applied to signal detection, including the affine invariant Riemannian metric, the log-Euclidean metric, and the Bures--Wasserstein (BW) metric, the last of which was recently extended to HPD manifolds. Riemannian gradient descent algorithms are proposed to solve the corresponding geometric means and medians, that play fundamental roles in the detection process. Simulations within the scenario using the ideal steering vector as the target signal provide compelling evidence that the BW detectors outperform the other geometric detectors as well as the conventional adaptive matched filter and adaptive normalized matched filter when observation data are limited. Further simulations demonstrate that the matrix-CFAR is robust in scenarios where the signal is mismatched. In addition to detection performances, robustness of the geometric detectors to outliers and computational complexity of the algorithms are analysed.

Prediction method of Soundscape Impressions using Environmental Sounds and Aerial Photographs

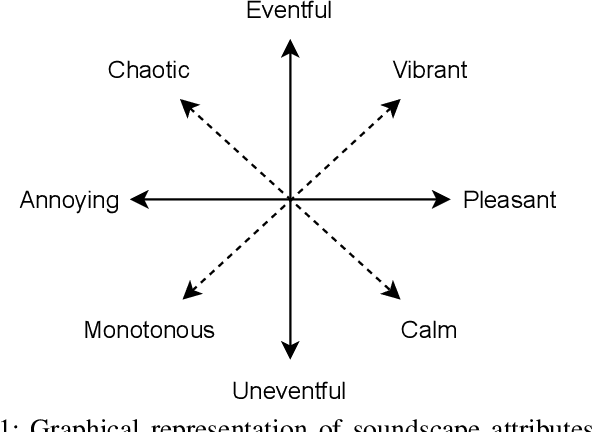
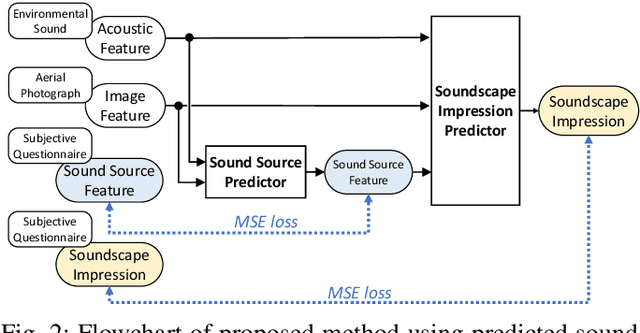
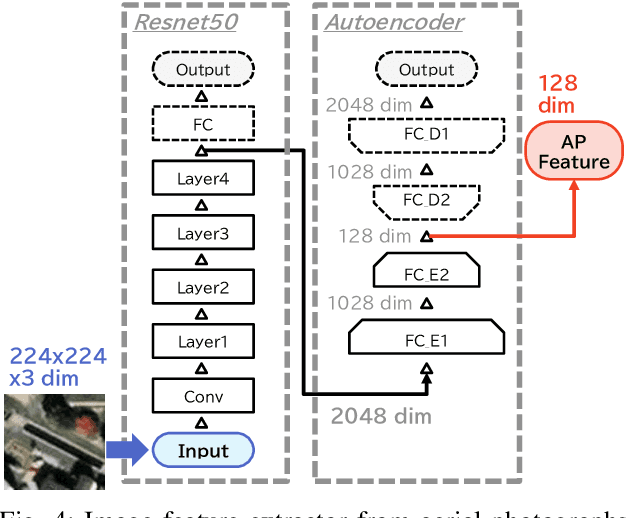
We investigate an method for quantifying city characteristics based on impressions of a sound environment. The quantification of the city characteristics will be beneficial to government policy planning, tourism projects, etc. In this study, we try to predict two soundscape impressions, meaning pleasantness and eventfulness, using sound data collected by the cloud-sensing method. The collected sounds comprise meta information of recording location using Global Positioning System. Furthermore, the soundscape impressions and sound-source features are separately assigned to the cloud-sensing sounds by assessments defined using Swedish Soundscape-Quality Protocol, assessing the quality of the acoustic environment. The prediction models are built using deep neural networks with multi-layer perceptron for the input of 10-second sound and the aerial photographs of its location. An acoustic feature comprises equivalent noise level and outputs of octave-band filters every second, and statistics of them in 10~s. An image feature is extracted from an aerial photograph using ResNet-50 and autoencoder architecture. We perform comparison experiments to demonstrate the benefit of each feature. As a result of the comparison, aerial photographs and sound-source features are efficient to predict impression information. Additionally, even if the sound-source features are predicted using acoustic and image features, the features also show fine results to predict the soundscape impression close to the result of oracle sound-source features.

Towards a median signal detector through the total Bregman divergence and its robust analysis

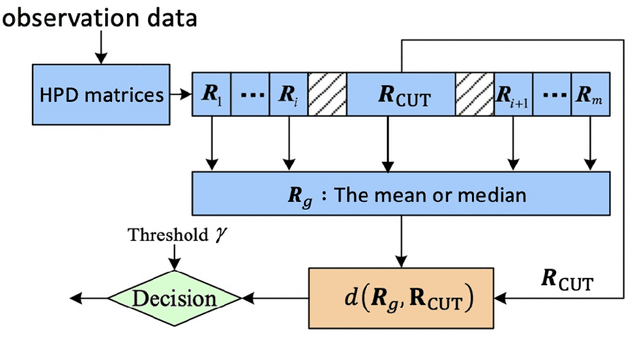
A novel family of geometric signal detectors are proposed through medians of the total Bregman divergence (TBD), which are shown advantageous over the conventional methods and their mean counterparts. By interpreting the observation data as Hermitian positive-definite (HPD) matrices, their mean or median play an essential role in signal detection. As is difficult to be solved analytically, we propose numerical solutions through Riemannian gradient descent algorithms or fixed-point algorithms. Beside detection performance, robustness of a detector to outliers is also of vital importance, which can often be analyzed via the influence functions. Introducing an orthogonal basis for Hermitian matrices, we are able to compute the corresponding influence functions analytically and exactly by solving a linear system, which is transformed from the governing matrix equation. Numerical simulations show that the TBD medians are more robust than their mean counterparts.

Unsupervised Learning Discriminative MIG Detectors in Nonhomogeneous Clutter

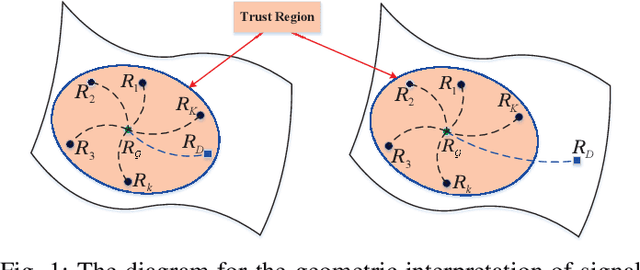
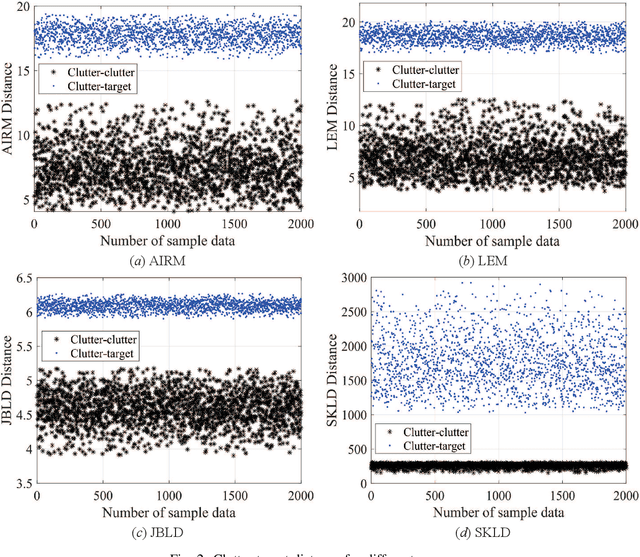
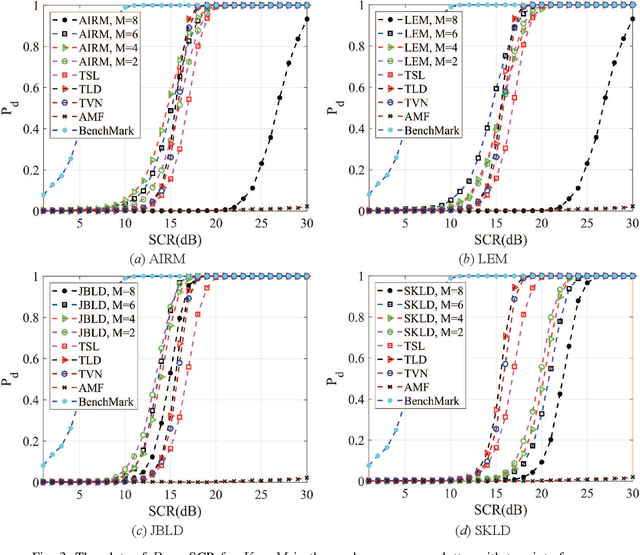
Principal component analysis (PCA) is a common used pattern analysis method that maps high-dimensional data into a lower-dimensional space maximizing the data variance, that results in the promotion of separability of data. Inspired by the principle of PCA, a novel type of learning discriminative matrix information geometry (MIG) detectors in the unsupervised scenario are developed, and applied to signal detection in nonhomogeneous environments. Hermitian positive-definite (HPD) matrices can be used to model the sample data, while the clutter covariance matrix is estimated by the geometric mean of a set of secondary HPD matrices. We define a projection that maps the HPD matrices in a high-dimensional manifold to a low-dimensional and more discriminative one to increase the degree of separation of HPD matrices by maximizing the data variance. Learning a mapping can be formulated as a two-step mini-max optimization problem in Riemannian manifolds, which can be solved by the Riemannian gradient descent algorithm. Three discriminative MIG detectors are illustrated with respect to different geometric measures, i.e., the Log-Euclidean metric, the Jensen--Bregman LogDet divergence and the symmetrized Kullback--Leibler divergence. Simulation results show that performance improvements of the novel MIG detectors can be achieved compared with the conventional detectors and their state-of-the-art counterparts within nonhomogeneous environments.

Target Detection within Nonhomogeneous Clutter via Total Bregman Divergence-Based Matrix Information Geometry Detectors

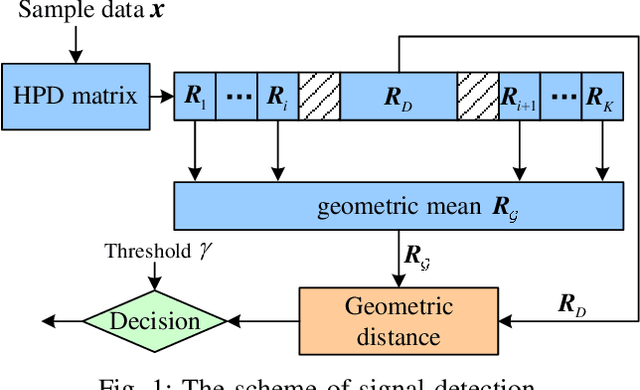
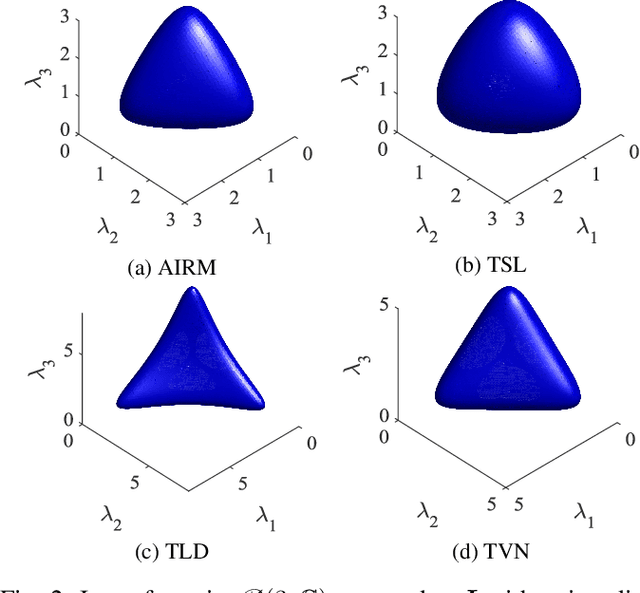
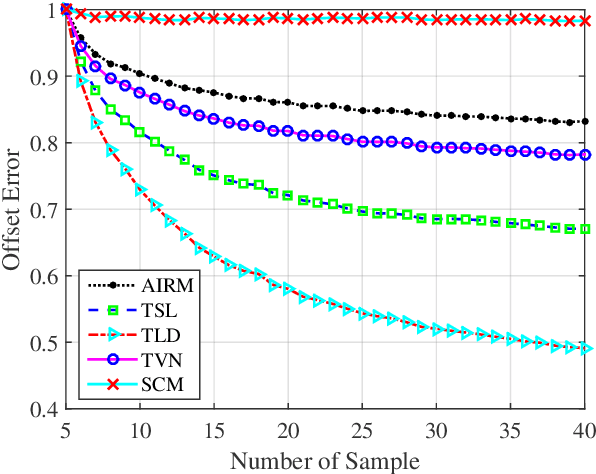
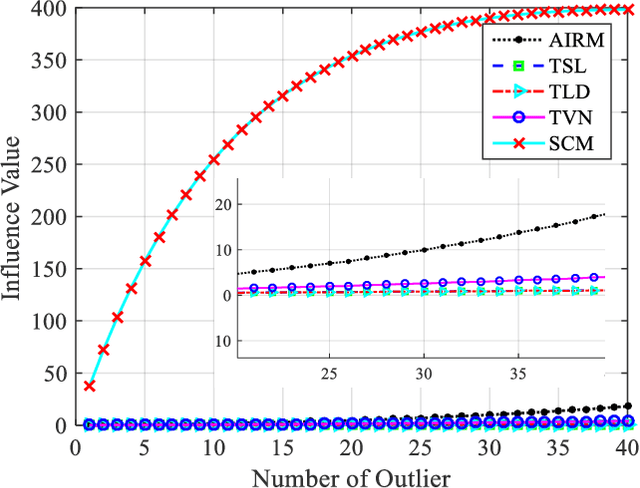
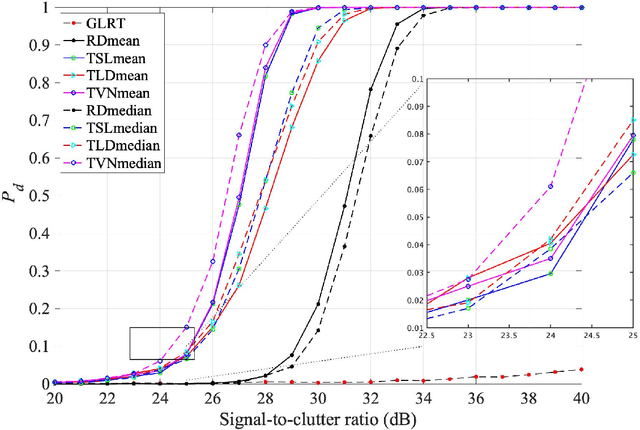
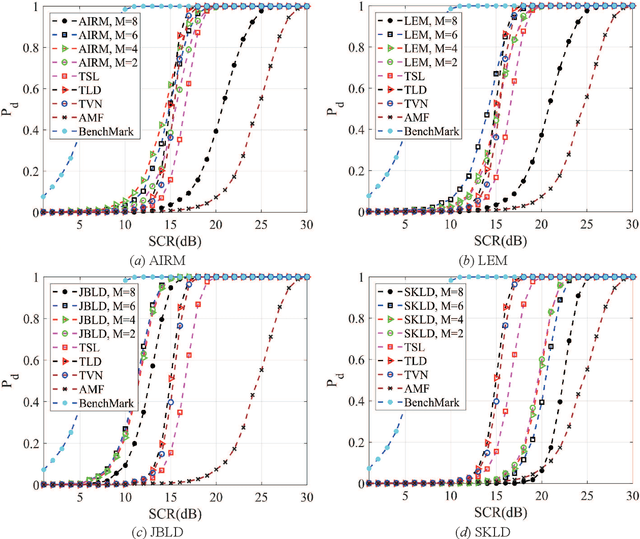
Information divergences are commonly used to measure the dissimilarity of two elements on a statistical manifold. Differentiable manifolds endowed with different divergences may possess different geometric properties, which can result in totally different performances in many practical applications. In this paper, we propose a total Bregman divergence-based matrix information geometry (TBD-MIG) detector and apply it to detect targets emerged into nonhomogeneous clutter. In particular, each sample data is assumed to be modeled as a Hermitian positive-definite (HPD) matrix and the clutter covariance matrix is estimated by the TBD mean of a set of secondary HPD matrices. We then reformulate the problem of signal detection as discriminating two points on the HPD matrix manifold. Three TBD-MIG detectors, referred to as the total square loss, the total log-determinant and the total von Neumann MIG detectors, are proposed, and they can achieve great performances due to their power of discrimination and robustness to interferences. Simulations show the advantage of the proposed TBD-MIG detectors in comparison with the geometric detector using an affine invariant Riemannian metric as well as the adaptive matched filter in nonhomogeneous clutter.