The Comparison of Riemannian Geometric Matrix-CFAR Signal Detectors
Paper and Code
Sep 27, 2024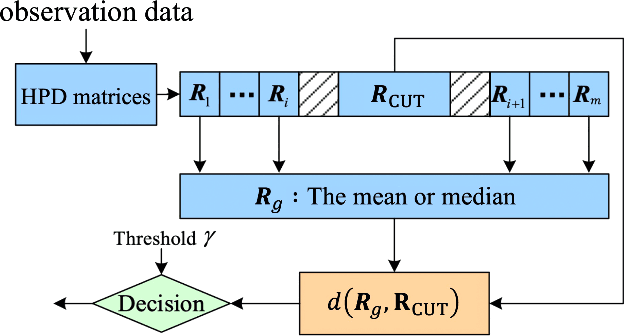
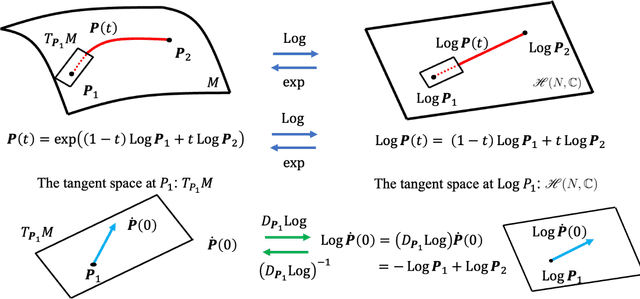
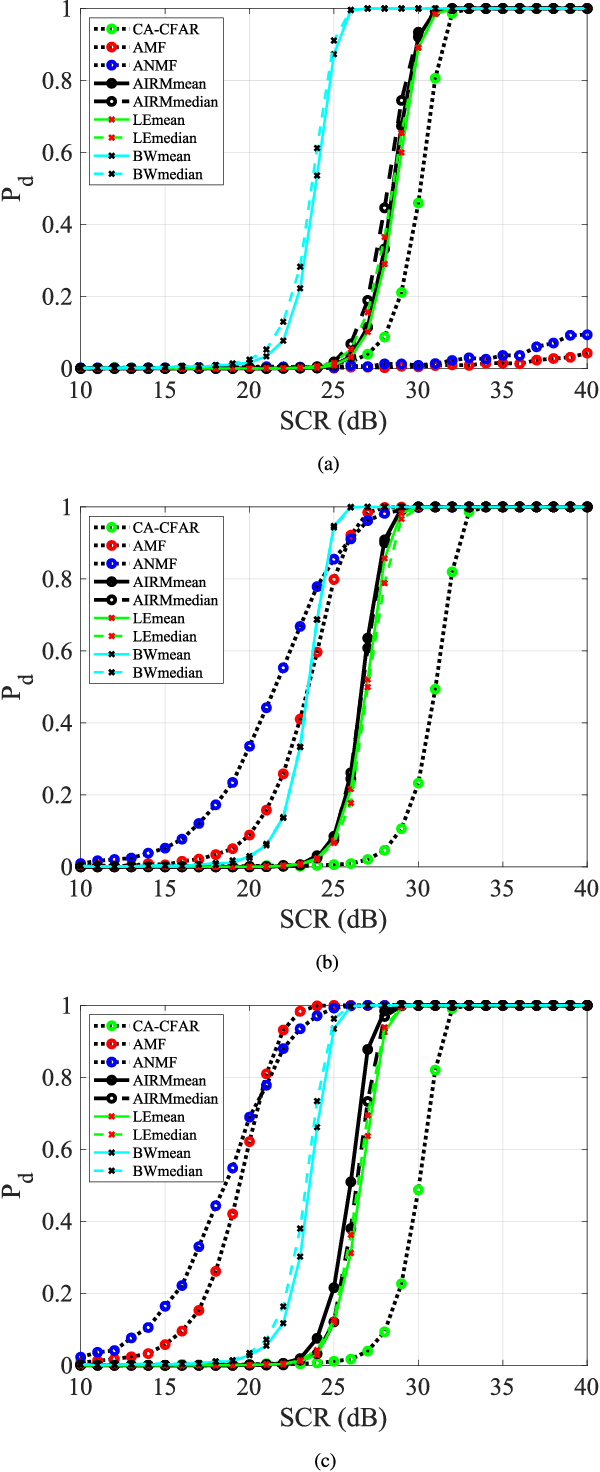
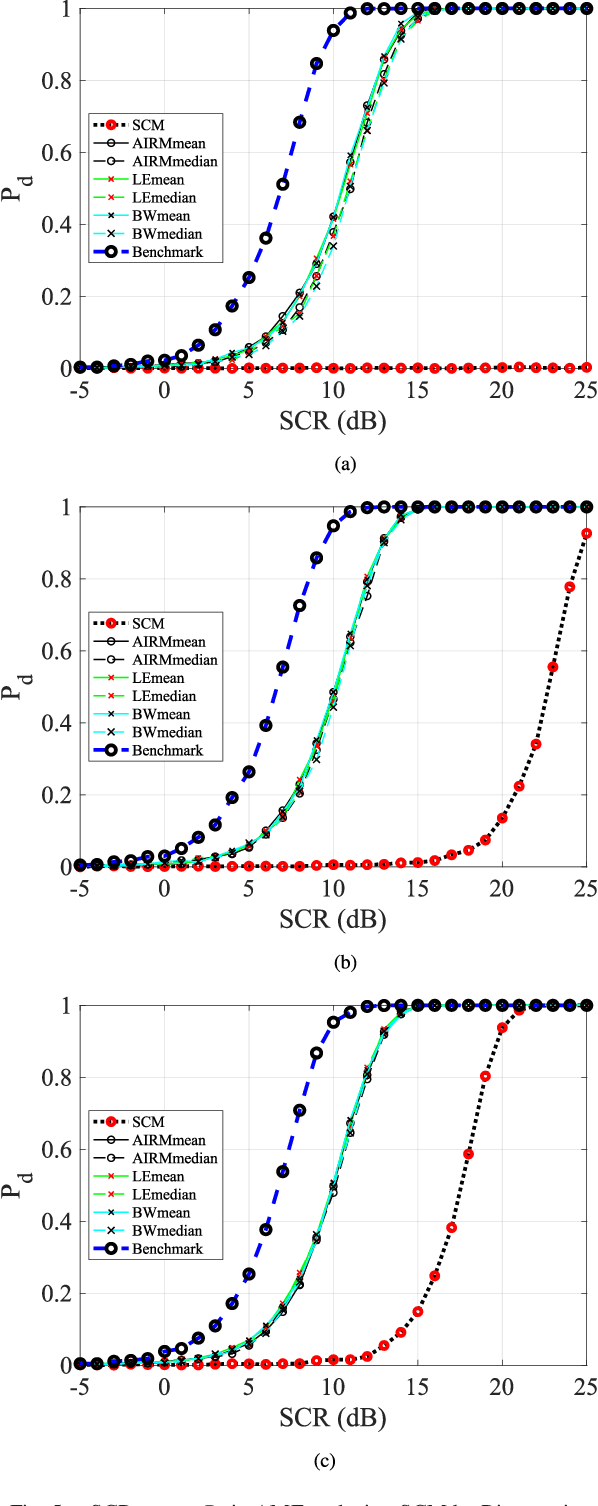
Essential characteristics of signal data can be captured by the autocovariance matrix, which, in the stationary scenarios, is Toeplitz Hermitian positive definite (HPD). In this paper, several well-known Riemannian geometric structures of HPD matrix manifolds are applied to signal detection, including the affine invariant Riemannian metric, the log-Euclidean metric, and the Bures--Wasserstein (BW) metric, the last of which was recently extended to HPD manifolds. Riemannian gradient descent algorithms are proposed to solve the corresponding geometric means and medians, that play fundamental roles in the detection process. Simulations within the scenario using the ideal steering vector as the target signal provide compelling evidence that the BW detectors outperform the other geometric detectors as well as the conventional adaptive matched filter and adaptive normalized matched filter when observation data are limited. Further simulations demonstrate that the matrix-CFAR is robust in scenarios where the signal is mismatched. In addition to detection performances, robustness of the geometric detectors to outliers and computational complexity of the algorithms are analysed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge