LDA-MIG Detectors for Maritime Targets in Nonhomogeneous Sea Clutter

This paper deals with the problem of detecting maritime targets embedded in nonhomogeneous sea clutter, where limited number of secondary data is available due to the heterogeneity of sea clutter. A class of linear discriminant analysis (LDA)-based matrix information geometry (MIG) detectors is proposed in the supervised scenario. As customary, Hermitian positive-definite (HPD) matrices are used to model the observational sample data, and the clutter covariance matrix of received dataset is estimated as geometric mean of the secondary HPD matrices. Given a set of training HPD matrices with class labels, that are elements of a higher-dimensional HPD matrix manifold, the LDA manifold projection learns a mapping from the higher-dimensional HPD matrix manifold to a lower-dimensional one subject to maximum discrimination. In the current study, the LDA manifold projection, with the cost function maximizing between-class distance while minimizing within-class distance, is formulated as an optimization problem in the Stiefel manifold. Four robust LDA-MIG detectors corresponding to different geometric measures are proposed. Numerical results based on both simulated radar clutter with interferences and real IPIX radar data show the advantage of the proposed LDA-MIG detectors against their counterparts without using LDA as well as the state-of-art maritime target detection methods in nonhomogeneous sea clutter.

Dual Power Spectrum Manifold and Toeplitz HPD Manifold: Enhancement and Analysis for Matrix CFAR Detection

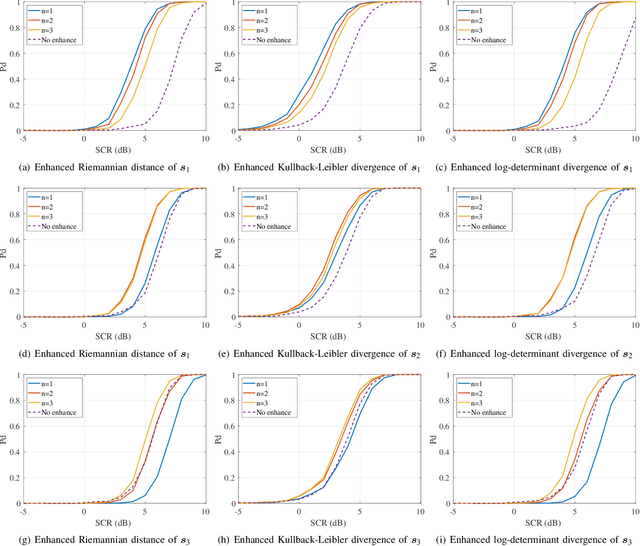
Recently, an innovative matrix CFAR detection scheme based on information geometry, also referred to as the geometric detector, has been developed speedily and exhibits distinct advantages in several practical applications. These advantages benefit from the geometry of the Toeplitz Hermitian positive definite (HPD) manifold $\mathcal{M}_{\mathcal{T}H_{++}}$, but the sophisticated geometry also results in some challenges for geometric detectors, such as the implementation of the enhanced detector to improve the SCR (signal-to-clutter ratio) and the analysis of the detection performance. To meet these challenges, this paper develops the dual power spectrum manifold $\mathcal{M}_{\text{P}}$ as the dual space of $\mathcal{M}_{\mathcal{T}H_{++}}$. For each affine invariant geometric measure on $\mathcal{M}_{\mathcal{T}H_{++}}$, we show that there exists an equivalent function named induced potential function on $\mathcal{M}_{\text{P}}$. By the induced potential function, the measurements of the dissimilarity between two matrices can be implemented on $\mathcal{M}_{\text{P}}$, and the geometric detectors can be reformulated as the form related to the power spectrum. The induced potential function leads to two contributions: 1) The enhancement of the geometric detector, which is formulated as an optimization problem concerning $\mathcal{M}_{\mathcal{T}H_{++}}$, is transformed to an equivalent and simpler optimization on $\mathcal{M}_{\text{P}}$. In the presented example of the enhancement, the closed-form solution, instead of the gradient descent method, is provided through the equivalent optimization. 2) The detection performance is analyzed based on $\mathcal{M}_{\text{P}}$, and the advantageous characteristics, which benefit the detection performance, can be deduced by analyzing the corresponding power spectrum to the maximal point of the induced potential function.

Origami-inspired soft twisting actuator

Soft actuators have shown great advantages in compliance and morphology matched for manipulation of delicate objects and inspection in a confined space. There is an unmet need for a soft actuator that can provide torsional motion to e.g. enlarge working space and increase degrees of freedom. Towards this goal, we present origami-inspired soft pneumatic actuators (OSPAs) made from silicone. The prototype can output a rotation of more than one revolution (up to 435{\deg}), larger than previous counterparts. We describe the design and fabrication method, build the kinematics models and simulation models, and analyze and optimize the parameters. Finally, we demonstrate the potentially extensive utility of OSPAs through their integration into a gripper capable of simultaneously grasping and lifting fragile or flat objects, a versatile robot arm capable of picking and placing items at the right angle with the twisting actuators, and a soft snake robot capable of changing attitude and directions by torsion of the twisting actuators.

Target Detection within Nonhomogeneous Clutter via Total Bregman Divergence-Based Matrix Information Geometry Detectors

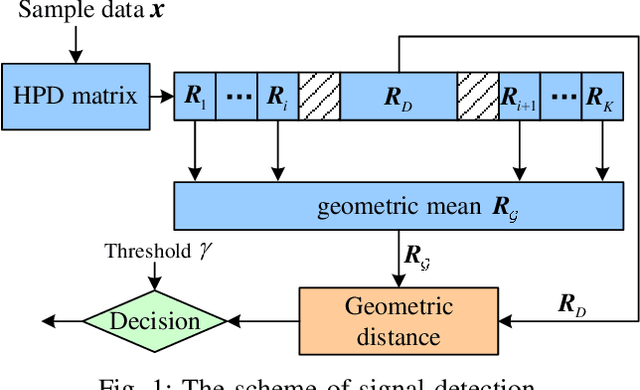
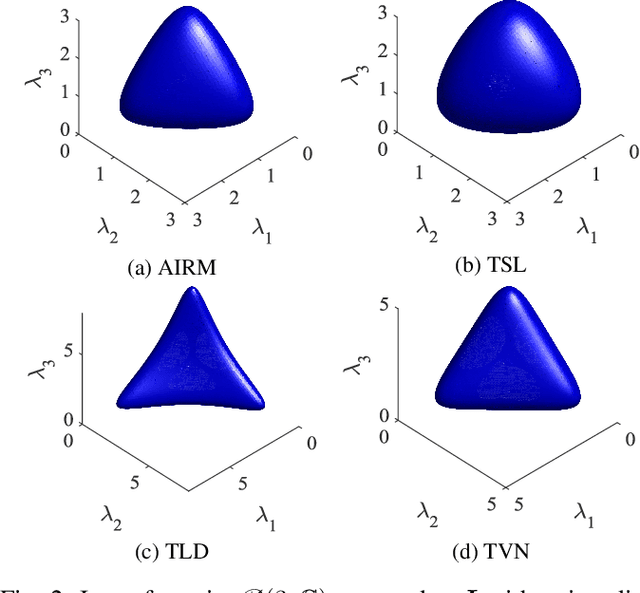
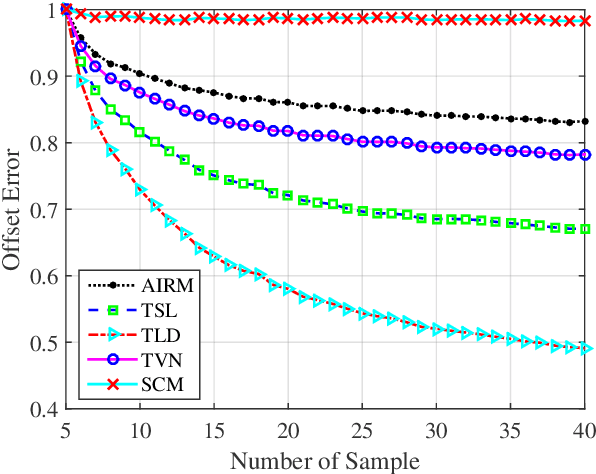
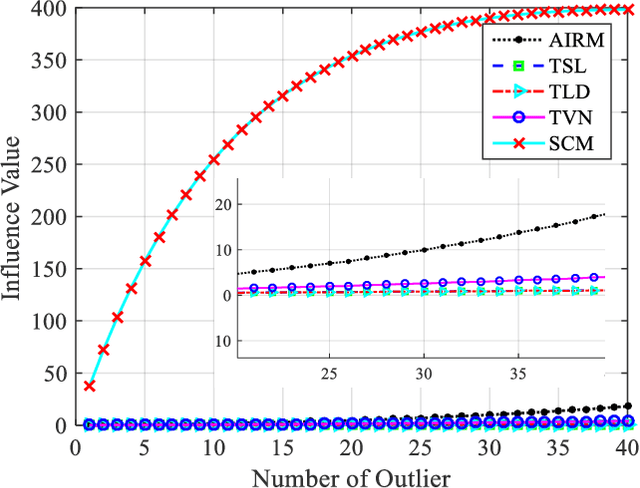
Information divergences are commonly used to measure the dissimilarity of two elements on a statistical manifold. Differentiable manifolds endowed with different divergences may possess different geometric properties, which can result in totally different performances in many practical applications. In this paper, we propose a total Bregman divergence-based matrix information geometry (TBD-MIG) detector and apply it to detect targets emerged into nonhomogeneous clutter. In particular, each sample data is assumed to be modeled as a Hermitian positive-definite (HPD) matrix and the clutter covariance matrix is estimated by the TBD mean of a set of secondary HPD matrices. We then reformulate the problem of signal detection as discriminating two points on the HPD matrix manifold. Three TBD-MIG detectors, referred to as the total square loss, the total log-determinant and the total von Neumann MIG detectors, are proposed, and they can achieve great performances due to their power of discrimination and robustness to interferences. Simulations show the advantage of the proposed TBD-MIG detectors in comparison with the geometric detector using an affine invariant Riemannian metric as well as the adaptive matched filter in nonhomogeneous clutter.