Rapid Machine Learning-Driven Detection of Pesticides and Dyes Using Raman Spectroscopy

The extensive use of pesticides and synthetic dyes poses critical threats to food safety, human health, and environmental sustainability, necessitating rapid and reliable detection methods. Raman spectroscopy offers molecularly specific fingerprints but suffers from spectral noise, fluorescence background, and band overlap, limiting its real-world applicability. Here, we propose a deep learning framework based on ResNet-18 feature extraction, combined with advanced classifiers, including XGBoost, SVM, and their hybrid integration, to detect pesticides and dyes from Raman spectroscopy, called MLRaman. The MLRaman with the CNN-XGBoost model achieved a predictive accuracy of 97.4% and a perfect AUC of 1.0, while it with the CNN-SVM model provided competitive results with robust class-wise discrimination. Dimensionality reduction analyses (PCA, t-SNE, UMAP) confirmed the separability of Raman embeddings across 10 analytes, including 7 pesticides and 3 dyes. Finally, we developed a user-friendly Streamlit application for real-time prediction, which successfully identified unseen Raman spectra from our independent experiments and also literature sources, underscoring strong generalization capacity. This study establishes a scalable, practical MLRaman model for multi-residue contaminant monitoring, with significant potential for deployment in food safety and environmental surveillance.

AI-driven materials design: a mini-review

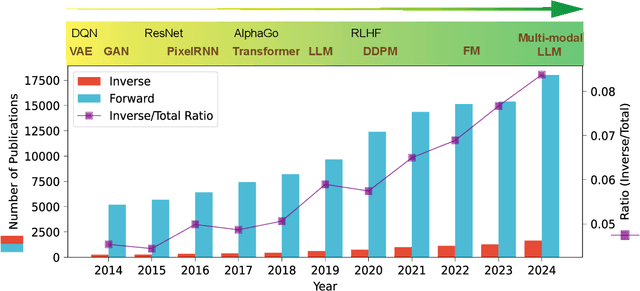
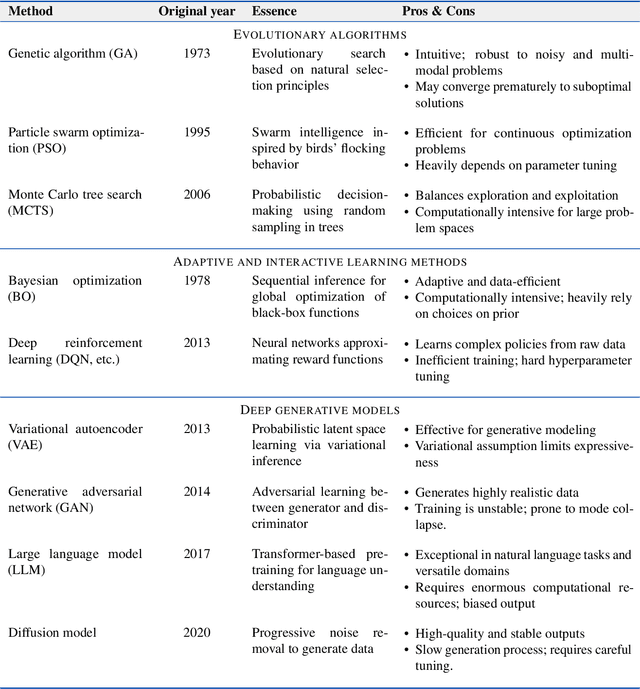
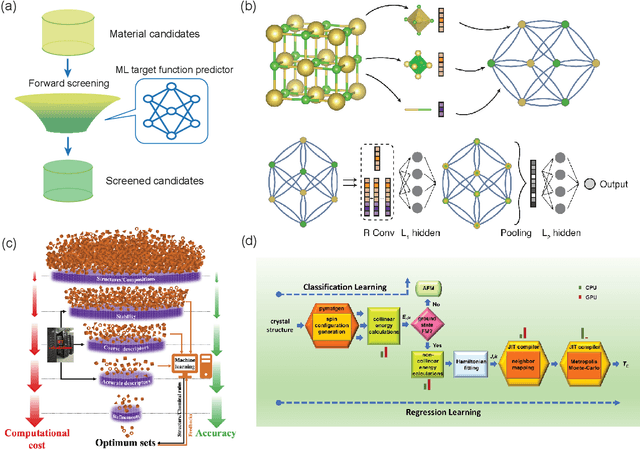
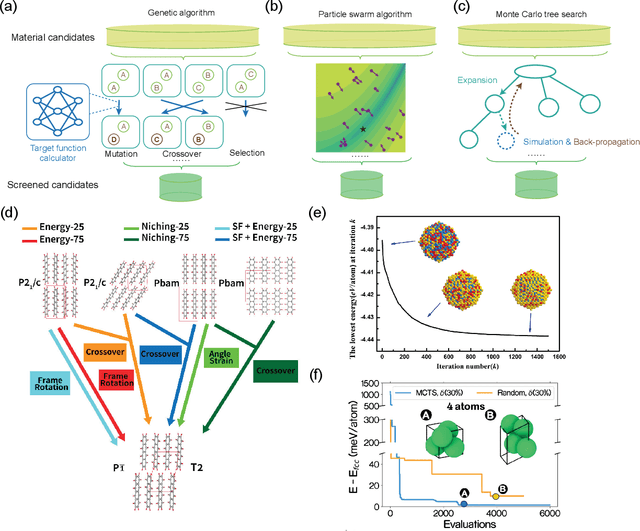
Materials design is an important component of modern science and technology, yet traditional approaches rely heavily on trial-and-error and can be inefficient. Computational techniques, enhanced by modern artificial intelligence (AI), have greatly accelerated the design of new materials. Among these approaches, inverse design has shown great promise in designing materials that meet specific property requirements. In this mini-review, we summarize key computational advancements for materials design over the past few decades. We follow the evolution of relevant materials design techniques, from high-throughput forward machine learning (ML) methods and evolutionary algorithms, to advanced AI strategies like reinforcement learning (RL) and deep generative models. We highlight the paradigm shift from conventional screening approaches to inverse generation driven by deep generative models. Finally, we discuss current challenges and future perspectives of materials inverse design. This review may serve as a brief guide to the approaches, progress, and outlook of designing future functional materials with technological relevance.

Structural Constraint Integration in Generative Model for Discovery of Quantum Material Candidates

Billions of organic molecules are known, but only a tiny fraction of the functional inorganic materials have been discovered, a particularly relevant problem to the community searching for new quantum materials. Recent advancements in machine-learning-based generative models, particularly diffusion models, show great promise for generating new, stable materials. However, integrating geometric patterns into materials generation remains a challenge. Here, we introduce Structural Constraint Integration in the GENerative model (SCIGEN). Our approach can modify any trained generative diffusion model by strategic masking of the denoised structure with a diffused constrained structure prior to each diffusion step to steer the generation toward constrained outputs. Furthermore, we mathematically prove that SCIGEN effectively performs conditional sampling from the original distribution, which is crucial for generating stable constrained materials. We generate eight million compounds using Archimedean lattices as prototype constraints, with over 10% surviving a multi-staged stability pre-screening. High-throughput density functional theory (DFT) on 26,000 survived compounds shows that over 50% passed structural optimization at the DFT level. Since the properties of quantum materials are closely related to geometric patterns, our results indicate that SCIGEN provides a general framework for generating quantum materials candidates.