MIG Median Detectors with Manifold Filter

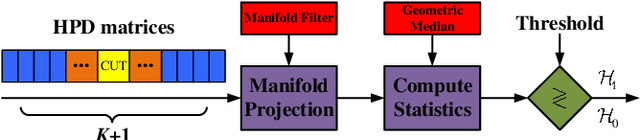
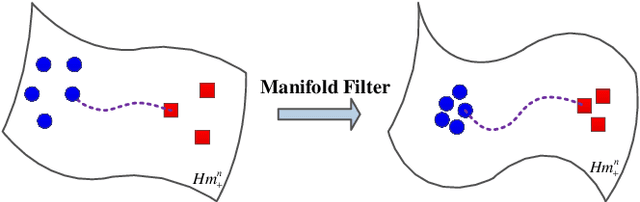
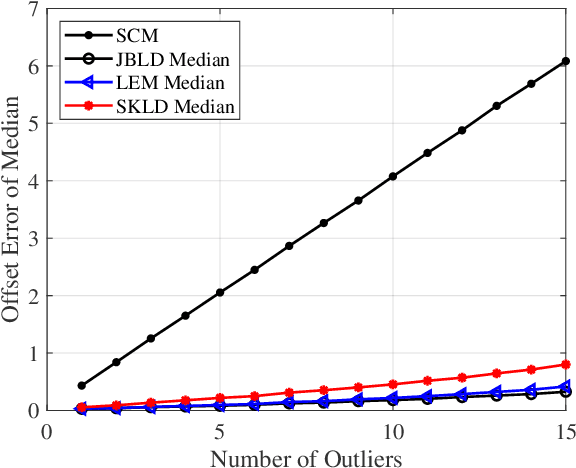
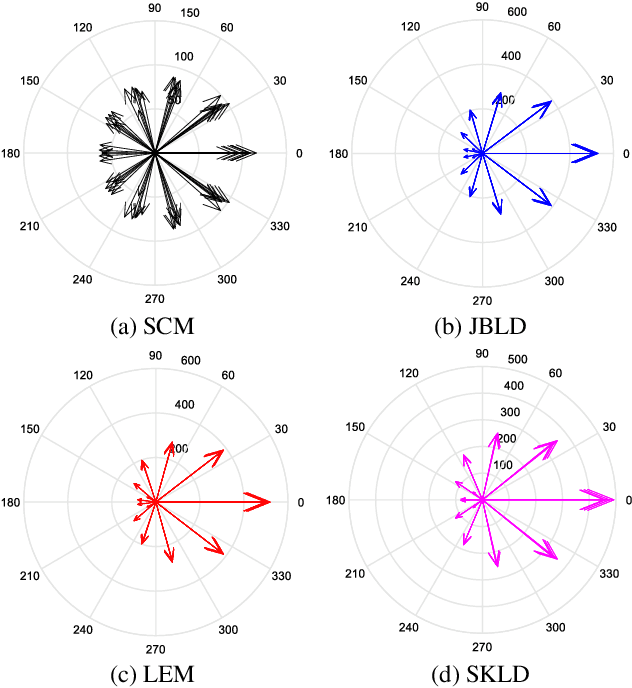
In this paper, we propose a class of median-based matrix information geometry (MIG) detectors with a manifold filter and apply them to signal detection in nonhomogeneous environments. As customary, the sample data is assumed to be modeled as Hermitian positive-definite (HPD) matrices, and the geometric median of a set of HPD matrices is interpreted as an estimate of the clutter covariance matrix (CCM). Then, the problem of signal detection can be reformulated as discriminating two points on the manifold of HPD matrices, one of which is the HPD matrix in the cell under test while the other represents the CCM. By manifold filter, we map a set of HPD matrices to another set of HPD matrices by weighting them, that consequently improves the discriminative power by reducing the intra-class distances while increasing the inter-class distances. Three MIG median detectors are designed by resorting to three geometric measures on the matrix manifold, and the corresponding geometric medians are shown to be robust to outliers. Numerical simulations show the advantage of the proposed MIG median detectors in comparison with their state-of-the-art counterparts as well as the conventional detectors in nonhomogeneous environments.