Verifying message-passing neural networks via topology-based bounds tightening
Paper and Code
Feb 21, 2024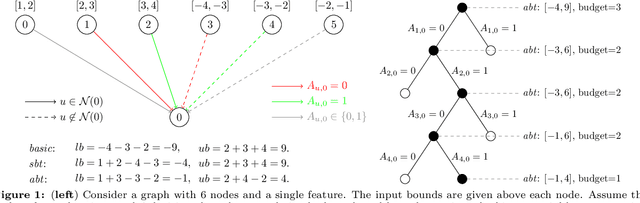
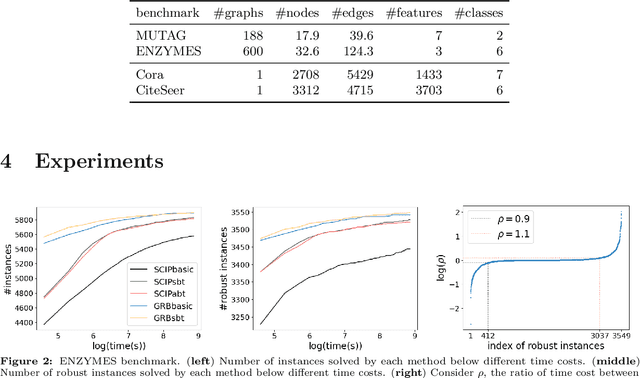
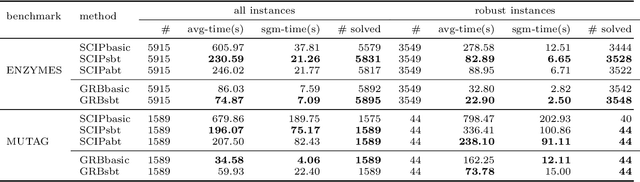
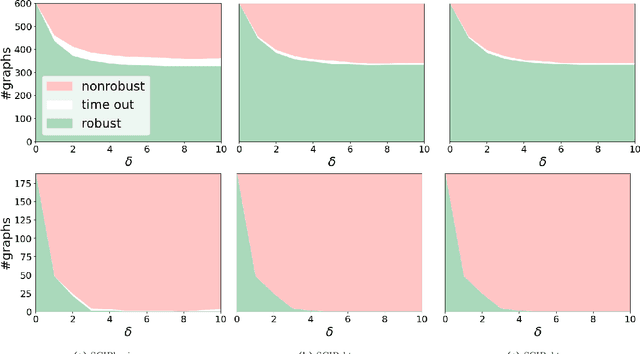
Since graph neural networks (GNNs) are often vulnerable to attack, we need to know when we can trust them. We develop a computationally effective approach towards providing robust certificates for message-passing neural networks (MPNNs) using a Rectified Linear Unit (ReLU) activation function. Because our work builds on mixed-integer optimization, it encodes a wide variety of subproblems, for example it admits (i) both adding and removing edges, (ii) both global and local budgets, and (iii) both topological perturbations and feature modifications. Our key technology, topology-based bounds tightening, uses graph structure to tighten bounds. We also experiment with aggressive bounds tightening to dynamically change the optimization constraints by tightening variable bounds. To demonstrate the effectiveness of these strategies, we implement an extension to the open-source branch-and-cut solver SCIP. We test on both node and graph classification problems and consider topological attacks that both add and remove edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge