Optimal quantisation of probability measures using maximum mean discrepancy

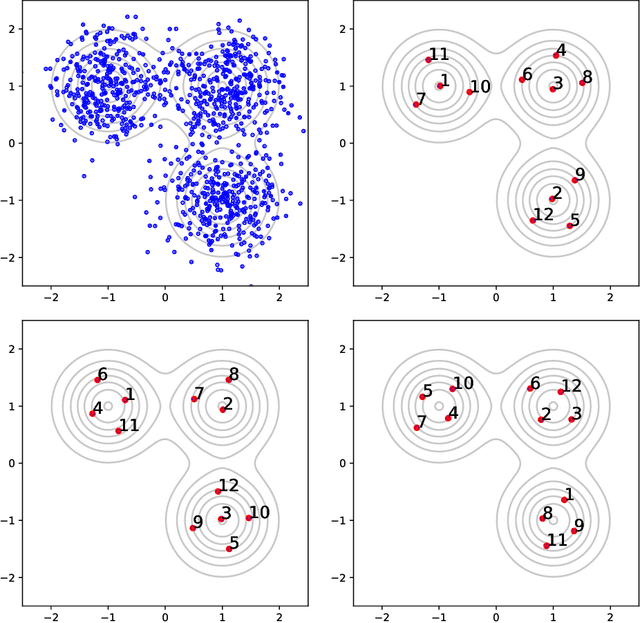
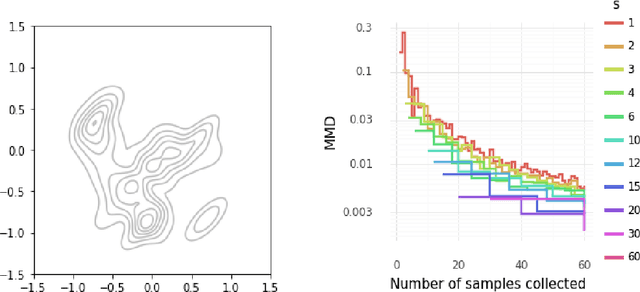
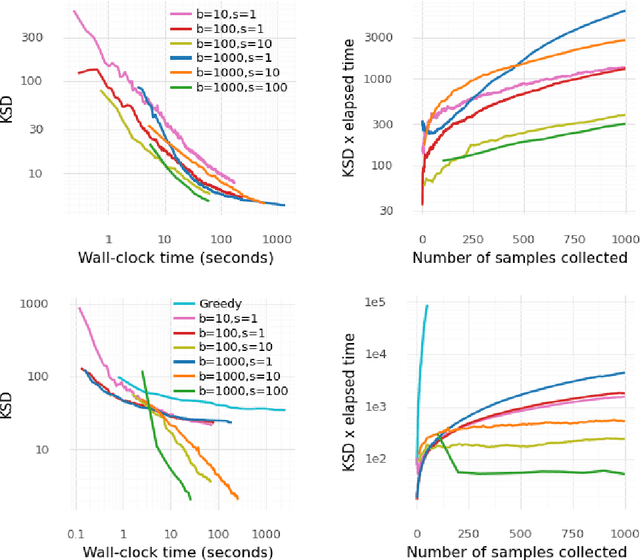
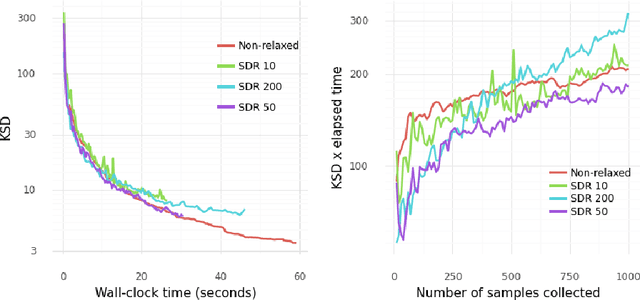
Several researchers have proposed minimisation of maximum mean discrepancy (MMD) as a method to quantise probability measures, i.e., to approximate a target distribution by a representative point set. Here we consider sequential algorithms that greedily minimise MMD over a discrete candidate set. We propose a novel non-myopic algorithm and, in order to both improve statistical efficiency and reduce computational cost, we investigate a variant that applies this technique to a mini-batch of the candidate set at each iteration. When the candidate points are sampled from the target, the consistency of these new algorithm - and their mini-batch variants - is established. We demonstrate the algorithms on a range of important computational problems, including optimisation of nodes in Bayesian cubature and the thinning of Markov chain output.

Optimal Thinning of MCMC Output

The use of heuristics to assess the convergence and compress the output of Markov chain Monte Carlo can be sub-optimal in terms of the empirical approximations that are produced. Typically a number of the initial states are attributed to "burn in" and removed, whilst the chain can be "thinned" if compression is also required. In this paper we consider the problem of selecting a subset of states, of fixed cardinality, such that the approximation provided by their empirical distribution is close to optimal. A novel method is proposed, based on greedy minimisation of a kernel Stein discrepancy, that is suitable for problems where heavy compression is required. Theoretical results guarantee consistency of the method and its effectiveness is demonstrated in the challenging context of parameter inference for ordinary differential equations. Software is available in the "Stein Thinning" package in both Python and MATLAB, and example code is included.

Considering discrepancy when calibrating a mechanistic electrophysiology model

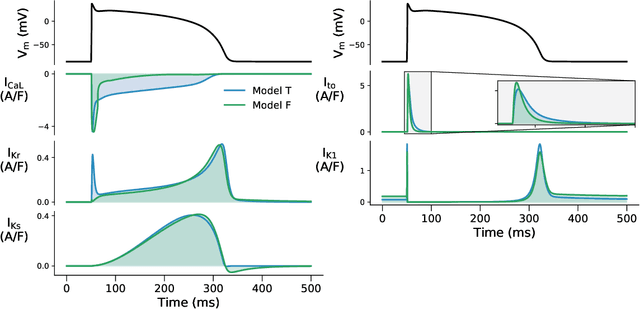
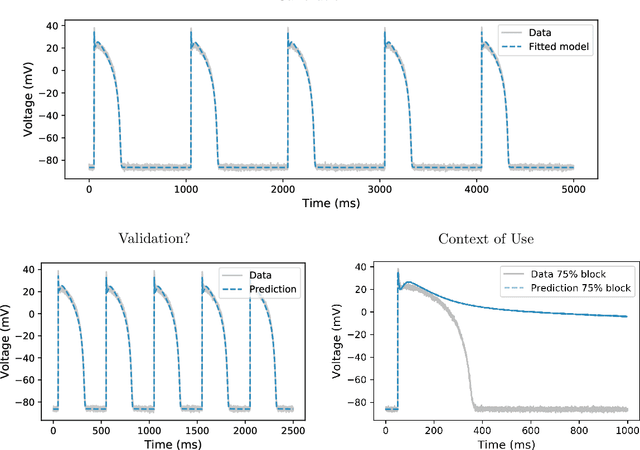
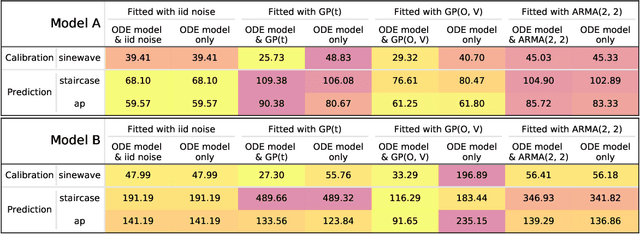
Uncertainty quantification (UQ) is a vital step in using mathematical models and simulations to take decisions. The field of cardiac simulation has begun to explore and adopt UQ methods to characterise uncertainty in model inputs and how that propagates through to outputs or predictions. In this perspective piece we draw attention to an important and under-addressed source of uncertainty in our predictions --- that of uncertainty in the model structure or the equations themselves. The difference between imperfect models and reality is termed model discrepancy, and we are often uncertain as to the size and consequences of this discrepancy. Here we provide two examples of the consequences of discrepancy when calibrating models at the ion channel and action potential scales. Furthermore, we attempt to account for this discrepancy when calibrating and validating an ion channel model using different methods, based on modelling the discrepancy using Gaussian processes (GPs) and autoregressive-moving-average (ARMA) models, then highlight the advantages and shortcomings of each approach. Finally, suggestions and lines of enquiry for future work are provided.