Measuring Sample Quality with Diffusions
Paper and Code
Feb 21, 2018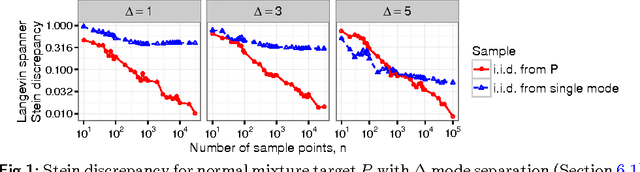
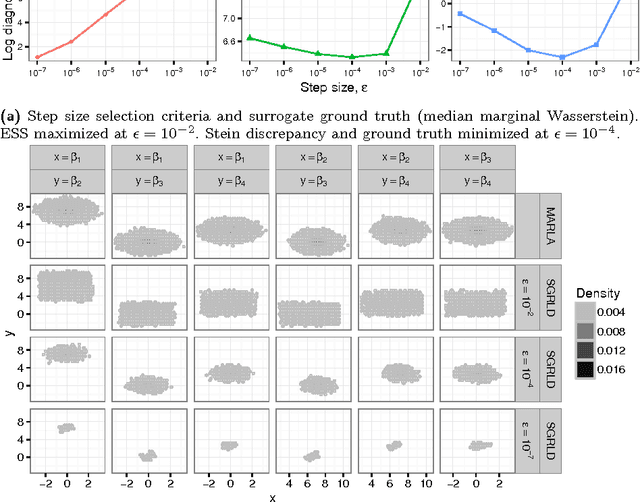
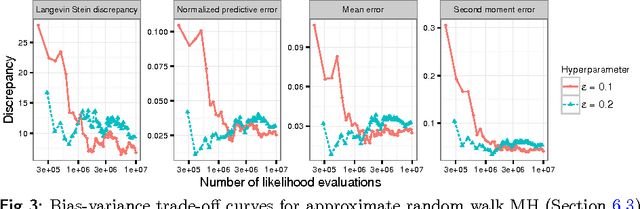
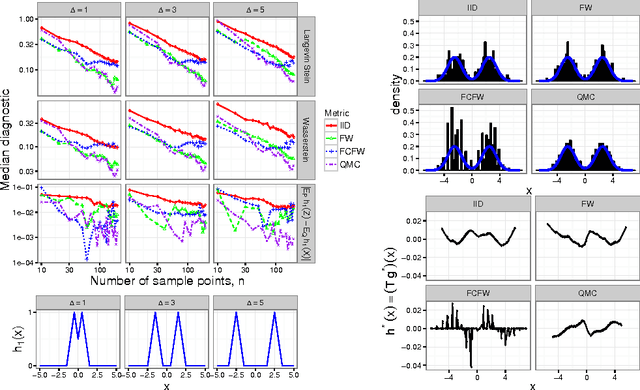
Stein's method for measuring convergence to a continuous target distribution relies on an operator characterizing the target and Stein factor bounds on the solutions of an associated differential equation. While such operators and bounds are readily available for a diversity of univariate targets, few multivariate targets have been analyzed. We introduce a new class of characterizing operators based on Ito diffusions and develop explicit multivariate Stein factor bounds for any target with a fast-coupling Ito diffusion. As example applications, we develop computable and convergence-determining diffusion Stein discrepancies for log-concave, heavy-tailed, and multimodal targets and use these quality measures to select the hyperparameters of biased Markov chain Monte Carlo (MCMC) samplers, compare random and deterministic quadrature rules, and quantify bias-variance tradeoffs in approximate MCMC. Our results establish a near-linear relationship between diffusion Stein discrepancies and Wasserstein distances, improving upon past work even for strongly log-concave targets. The exposed relationship between Stein factors and Markov process coupling may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge