Hybrid Pooling and Convolutional Network for Improving Accuracy and Training Convergence Speed in Object Detection

This paper introduces HPC-Net, a high-precision and rapidly convergent object detection network.

Consistent Collaborative Filtering via Tensor Decomposition

Collaborative filtering is the de facto standard for analyzing users' activities and building recommendation systems for items. In this work we develop Sliced Anti-symmetric Decomposition (SAD), a new model for collaborative filtering based on implicit feedback. In contrast to traditional techniques where a latent representation of users (user vectors) and items (item vectors) are estimated, SAD introduces one additional latent vector to each item, using a novel three-way tensor view of user-item interactions. This new vector extends user-item preferences calculated by standard dot products to general inner products, producing interactions between items when evaluating their relative preferences. SAD reduces to state-of-the-art (SOTA) collaborative filtering models when the vector collapses to one, while in this paper we allow its value to be estimated from data. The proposed SAD model is simple, resulting in an efficient group stochastic gradient descent (SGD) algorithm. We demonstrate the efficiency of SAD in both simulated and real world datasets containing over 1M user-item interactions. By comparing SAD with seven alternative SOTA collaborative filtering models, we show that SAD is able to more consistently estimate personalized preferences.

Fast moment estimation for generalized latent Dirichlet models

We develop a generalized method of moments (GMM) approach for fast parameter estimation in a new class of Dirichlet latent variable models with mixed data types. Parameter estimation via GMM has been demonstrated to have computational and statistical advantages over alternative methods, such as expectation maximization, variational inference, and Markov chain Monte Carlo. The key computational advan- tage of our method (MELD) is that parameter estimation does not require instantiation of the latent variables. Moreover, a representational advantage of the GMM approach is that the behavior of the model is agnostic to distributional assumptions of the observations. We derive population moment conditions after marginalizing out the sample-specific Dirichlet latent variables. The moment conditions only depend on component mean parameters. We illustrate the utility of our approach on simulated data, comparing results from MELD to alternative methods, and we show the promise of our approach through the application of MELD to several data sets.

Bayesian group latent factor analysis with structured sparsity

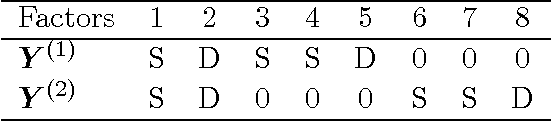
Latent factor models are the canonical statistical tool for exploratory analyses of low-dimensional linear structure for an observation matrix with p features across n samples. We develop a structured Bayesian group factor analysis model that extends the factor model to multiple coupled observation matrices; in the case of two observations, this reduces to a Bayesian model of canonical correlation analysis. The main contribution of this work is to carefully define a structured Bayesian prior that encourages both element-wise and column-wise shrinkage and leads to desirable behavior on high-dimensional data. In particular, our model puts a structured prior on the joint factor loading matrix, regularizing at three levels, which enables element-wise sparsity and unsupervised recovery of latent factors corresponding to structured variance across arbitrary subsets of the observations. In addition, our structured prior allows for both dense and sparse latent factors so that covariation among either all features or only a subset of features can both be recovered. We use fast parameter-expanded expectation-maximization for parameter estimation in this model. We validate our method on both simulated data with substantial structure and real data, comparing against a number of state-of-the-art approaches. These results illustrate useful properties of our model, including i) recovering sparse signal in the presence of dense effects; ii) the ability to scale naturally to large numbers of observations; iii) flexible observation- and factor-specific regularization to recover factors with a wide variety of sparsity levels and percentage of variance explained; and iv) tractable inference that scales to modern genomic and document data sizes.

Differential gene co-expression networks via Bayesian biclustering models

Identifying latent structure in large data matrices is essential for exploring biological processes. Here, we consider recovering gene co-expression networks from gene expression data, where each network encodes relationships between genes that are locally co-regulated by shared biological mechanisms. To do this, we develop a Bayesian statistical model for biclustering to infer subsets of co-regulated genes whose covariation may be observed in only a subset of the samples. Our biclustering method, BicMix, has desirable properties, including allowing overcomplete representations of the data, computational tractability, and jointly modeling unknown confounders and biological signals. Compared with related biclustering methods, BicMix recovers latent structure with higher precision across diverse simulation scenarios. Further, we develop a method to recover gene co-expression networks from the estimated sparse biclustering matrices. We apply BicMix to breast cancer gene expression data and recover a gene co-expression network that is differential across ER+ and ER- samples.