Logistic-beta processes for modeling dependent random probabilities with beta marginals

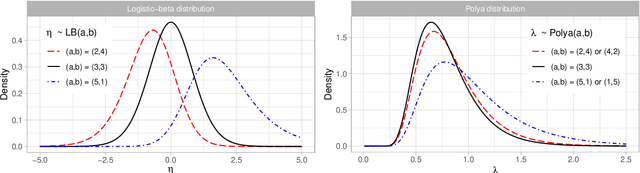
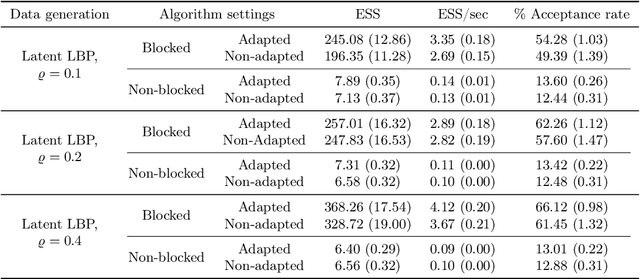
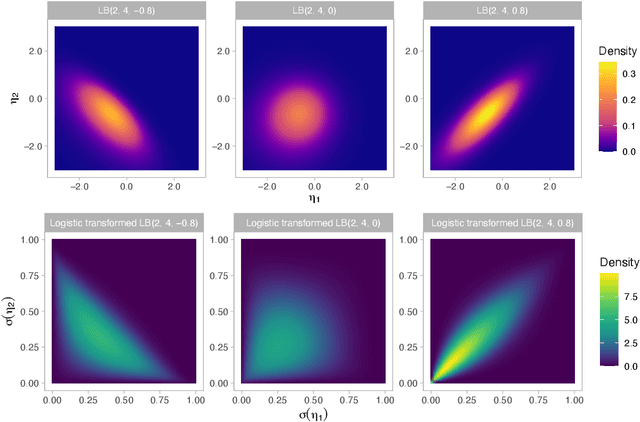
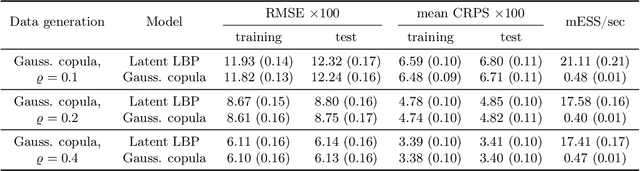
The beta distribution serves as a canonical tool for modeling probabilities and is extensively used in statistics and machine learning, especially in the field of Bayesian nonparametrics. Despite its widespread use, there is limited work on flexible and computationally convenient stochastic process extensions for modeling dependent random probabilities. We propose a novel stochastic process called the logistic-beta process, whose logistic transformation yields a stochastic process with common beta marginals. Similar to the Gaussian process, the logistic-beta process can model dependence on both discrete and continuous domains, such as space or time, and has a highly flexible dependence structure through correlation kernels. Moreover, its normal variance-mean mixture representation leads to highly effective posterior inference algorithms. The flexibility and computational benefits of logistic-beta processes are demonstrated through nonparametric binary regression simulation studies. Furthermore, we apply the logistic-beta process in modeling dependent Dirichlet processes, and illustrate its application and benefits through Bayesian density regression problems in a toxicology study.