Proximal Algorithms for Accelerated Langevin Dynamics

We develop a novel class of MCMC algorithms based on a stochastized Nesterov scheme. With an appropriate addition of noise, the result is a time-inhomogeneous underdamped Langevin equation, which we prove emits a specified target distribution as its invariant measure. Convergence rates to stationarity under Wasserstein-2 distance are established as well. Metropolis-adjusted and stochastic gradient versions of the proposed Langevin dynamics are also provided. Experimental illustrations show superior performance of the proposed method over typical Langevin samplers for different models in statistics and image processing including better mixing of the resulting Markov chains.

System Identification Using the Signed Cumulative Distribution Transform In Structural Health Monitoring Applications

This paper presents a novel, data-driven approach to identifying partial differential equation (PDE) parameters of a dynamical system in structural health monitoring applications. Specifically, we adopt a mathematical "transport" model of the sensor data that allows us to accurately estimate the model parameters, including those associated with structural damage. This is accomplished by means of a newly-developed transform, the signed cumulative distribution transform (SCDT), which is shown to convert the general, nonlinear parameter estimation problem into a simple linear regression. This approach has the additional practical advantage of requiring no a priori knowledge of the source of the excitation (or, alternatively, the initial conditions). By using training sensor data, we devise a coarse regression procedure to recover different PDE parameters from a single sensor measurement. Numerical experiments show that the proposed regression procedure is capable of detecting and estimating PDE parameters with superior accuracy compared to a number of recently developed "Deep Learning" methods. The Python implementation of the proposed system identification technique is integrated as a part of the software package PyTransKit (https://github.com/rohdelab/PyTransKit).

Riesz-Quincunx-UNet Variational Auto-Encoder for Satellite Image Denoising

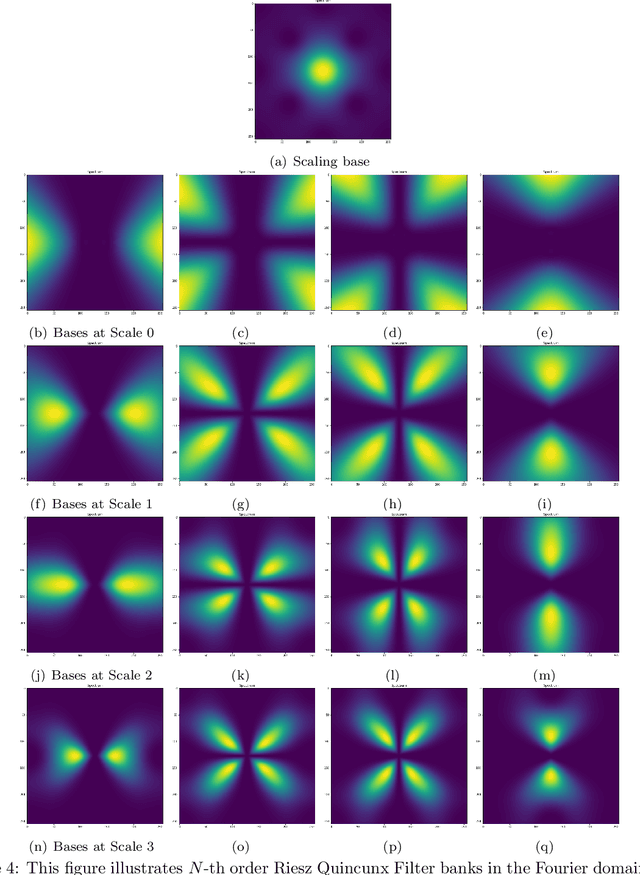
Multiresolution deep learning approaches, such as the U-Net architecture, have achieved high performance in classifying and segmenting images. However, these approaches do not provide a latent image representation and cannot be used to decompose, denoise, and reconstruct image data. The U-Net and other convolutional neural network (CNNs) architectures commonly use pooling to enlarge the receptive field, which usually results in irreversible information loss. This study proposes to include a Riesz-Quincunx (RQ) wavelet transform, which combines 1) higher-order Riesz wavelet transform and 2) orthogonal Quincunx wavelets (which have both been used to reduce blur in medical images) inside the U-net architecture, to reduce noise in satellite images and their time-series. In the transformed feature space, we propose a variational approach to understand how random perturbations of the features affect the image to further reduce noise. Combining both approaches, we introduce a hybrid RQUNet-VAE scheme for image and time series decomposition used to reduce noise in satellite imagery. We present qualitative and quantitative experimental results that demonstrate that our proposed RQUNet-VAE was more effective at reducing noise in satellite imagery compared to other state-of-the-art methods. We also apply our scheme to several applications for multi-band satellite images, including: image denoising, image and time-series decomposition by diffusion and image segmentation.

Generalized Intersection Algorithms with Fixpoints for Image Decomposition Learning

In image processing, classical methods minimize a suitable functional that balances between computational feasibility (convexity of the functional is ideal) and suitable penalties reflecting the desired image decomposition. The fact that algorithms derived from such minimization problems can be used to construct (deep) learning architectures has spurred the development of algorithms that can be trained for a specifically desired image decomposition, e.g. into cartoon and texture. While many such methods are very successful, theoretical guarantees are only scarcely available. To this end, in this contribution, we formalize a general class of intersection point problems encompassing a wide range of (learned) image decomposition models, and we give an existence result for a large subclass of such problems, i.e. giving the existence of a fixpoint of the corresponding algorithm. This class generalizes classical model-based variational problems, such as the TV-l2 -model or the more general TV-Hilbert model. To illustrate the potential for learned algorithms, novel (non learned) choices within our class show comparable results in denoising and texture removal.