Linear optimal transport subspaces for point set classification

Learning from point sets is an essential component in many computer vision and machine learning applications. Native, unordered, and permutation invariant set structure space is challenging to model, particularly for point set classification under spatial deformations. Here we propose a framework for classifying point sets experiencing certain types of spatial deformations, with a particular emphasis on datasets featuring affine deformations. Our approach employs the Linear Optimal Transport (LOT) transform to obtain a linear embedding of set-structured data. Utilizing the mathematical properties of the LOT transform, we demonstrate its capacity to accommodate variations in point sets by constructing a convex data space, effectively simplifying point set classification problems. Our method, which employs a nearest-subspace algorithm in the LOT space, demonstrates label efficiency, non-iterative behavior, and requires no hyper-parameter tuning. It achieves competitive accuracies compared to state-of-the-art methods across various point set classification tasks. Furthermore, our approach exhibits robustness in out-of-distribution scenarios where training and test distributions vary in terms of deformation magnitudes.

System Identification Using the Signed Cumulative Distribution Transform In Structural Health Monitoring Applications

This paper presents a novel, data-driven approach to identifying partial differential equation (PDE) parameters of a dynamical system in structural health monitoring applications. Specifically, we adopt a mathematical "transport" model of the sensor data that allows us to accurately estimate the model parameters, including those associated with structural damage. This is accomplished by means of a newly-developed transform, the signed cumulative distribution transform (SCDT), which is shown to convert the general, nonlinear parameter estimation problem into a simple linear regression. This approach has the additional practical advantage of requiring no a priori knowledge of the source of the excitation (or, alternatively, the initial conditions). By using training sensor data, we devise a coarse regression procedure to recover different PDE parameters from a single sensor measurement. Numerical experiments show that the proposed regression procedure is capable of detecting and estimating PDE parameters with superior accuracy compared to a number of recently developed "Deep Learning" methods. The Python implementation of the proposed system identification technique is integrated as a part of the software package PyTransKit (https://github.com/rohdelab/PyTransKit).

The Radon Signed Cumulative Distribution Transform and its applications in classification of Signed Images

Here we describe a new image representation technique based on the mathematics of transport and optimal transport. The method relies on the combination of the well-known Radon transform for images and a recent signal representation method called the Signed Cumulative Distribution Transform. The newly proposed method generalizes previous transport-related image representation methods to arbitrary functions (images), and thus can be used in more applications. We describe the new transform, and some of its mathematical properties and demonstrate its ability to partition image classes with real and simulated data. In comparison to existing transport transform methods, as well as deep learning-based classification methods, the new transform more accurately represents the information content of signed images, and thus can be used to obtain higher classification accuracies. The implementation of the proposed method in Python language is integrated as a part of the software package PyTransKit, available on Github.

A sliced-Wasserstein distance-based approach for out-of-class-distribution detection

There exist growing interests in intelligent systems for numerous medical imaging, image processing, and computer vision applications, such as face recognition, medical diagnosis, character recognition, and self-driving cars, among others. These applications usually require solving complex classification problems involving complex images with unknown data generative processes. In addition to recent successes of the current classification approaches relying on feature engineering and deep learning, several shortcomings of them, such as the lack of robustness, generalizability, and interpretability, have also been observed. These methods often require extensive training data, are computationally expensive, and are vulnerable to out-of-distribution samples, e.g., adversarial attacks. Recently, an accurate, data-efficient, computationally efficient, and robust transport-based classification approach has been proposed, which describes a generative model-based problem formulation and closed-form solution for a specific category of classification problems. However, all these approaches lack mechanisms to detect test samples outside the class distributions used during training. In real-world settings, where the collected training samples are unable to exhaust or cover all classes, the traditional classification schemes are unable to handle the unseen classes effectively, which is especially an important issue for safety-critical systems, such as self-driving and medical imaging diagnosis. In this work, we propose a method for detecting out-of-class distributions based on the distribution of sliced-Wasserstein distance from the Radon Cumulative Distribution Transform (R-CDT) subspace. We tested our method on the MNIST and two medical image datasets and reported better accuracy than the state-of-the-art methods without an out-of-class distribution detection procedure.

Geodesic Properties of a Generalized Wasserstein Embedding for Time Series Analysis

Transport-based metrics and related embeddings (transforms) have recently been used to model signal classes where nonlinear structures or variations are present. In this paper, we study the geodesic properties of time series data with a generalized Wasserstein metric and the geometry related to their signed cumulative distribution transforms in the embedding space. Moreover, we show how understanding such geometric characteristics can provide added interpretability to certain time series classifiers, and be an inspiration for more robust classifiers.

End-to-End Signal Classification in Signed Cumulative Distribution Transform Space

This paper presents a new end-to-end signal classification method using the signed cumulative distribution transform (SCDT). We adopt a transport-based generative model to define the classification problem. We then make use of mathematical properties of the SCDT to render the problem easier in transform domain, and solve for the class of an unknown sample using a nearest local subspace (NLS) search algorithm in SCDT domain. Experiments show that the proposed method provides high accuracy classification results while being data efficient, robust to out-of-distribution samples, and competitive in terms of computational complexity with respect to the deep learning end-to-end classification methods. The implementation of the proposed method in Python language is integrated as a part of the software package PyTransKit (https://github.com/rohdelab/PyTransKit).

Local Sliced-Wasserstein Feature Sets for Illumination-invariant Face Recognition

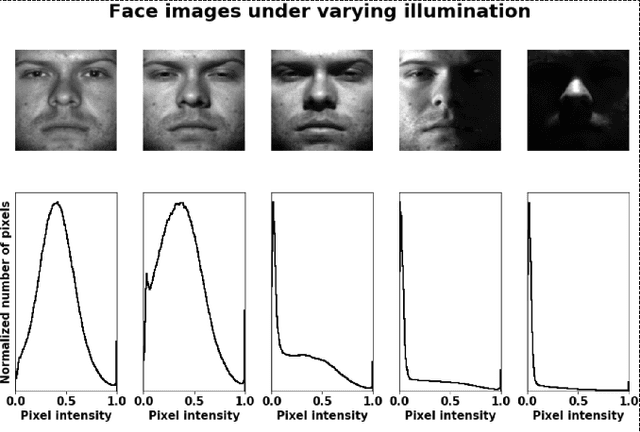
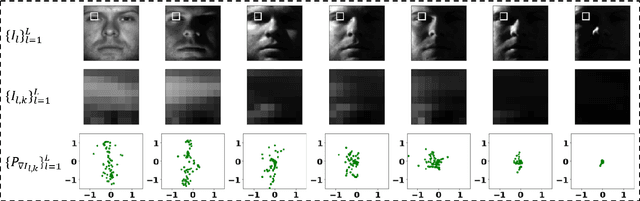
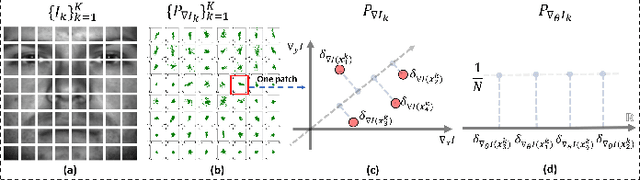
We present a new method for face recognition from digital images acquired under varying illumination conditions. The method is based on mathematical modeling of local gradient distributions using the Radon Cumulative Distribution Transform (R-CDT). We demonstrate that lighting variations cause certain types of deformations of local image gradient distributions which, when expressed in R-CDT domain, can be modeled as a subspace. Face recognition is then performed using a nearest subspace in R-CDT domain of local gradient distributions. Experiment results demonstrate the proposed method outperforms other alternatives in several face recognition tasks with challenging illumination conditions. Python code implementing the proposed method is available, which is integrated as a part of the software package PyTransKit.

Invariance encoding in sliced-Wasserstein space for image classification with limited training data

Deep convolutional neural networks (CNNs) are broadly considered to be state-of-the-art generic end-to-end image classification systems. However, they are known to underperform when training data are limited and thus require data augmentation strategies that render the method computationally expensive and not always effective. Rather than using a data augmentation strategy to encode invariances as typically done in machine learning, here we propose to mathematically augment a nearest subspace classification model in sliced-Wasserstein space by exploiting certain mathematical properties of the Radon Cumulative Distribution Transform (R-CDT), a recently introduced image transform. We demonstrate that for a particular type of learning problem, our mathematical solution has advantages over data augmentation with deep CNNs in terms of classification accuracy and computational complexity, and is particularly effective under a limited training data setting. The method is simple, effective, computationally efficient, non-iterative, and requires no parameters to be tuned. Python code implementing our method is available at https://github.com/rohdelab/mathematical_augmentation. Our method is integrated as a part of the software package PyTransKit, which is available at https://github.com/rohdelab/PyTransKit.

Nearest Subspace Search in The Signed Cumulative Distribution Transform Space for 1D Signal Classification

This paper presents a new method to classify 1D signals using the signed cumulative distribution transform (SCDT). The proposed method exploits certain linearization properties of the SCDT to render the problem easier to solve in the SCDT space. The method uses the nearest subspace search technique in the SCDT domain to provide a non-iterative, effective, and simple to implement classification algorithm. Experiments show that the proposed technique outperforms the state-of-the-art neural networks using a very low number of training samples and is also robust to out-of-distribution examples on simulated data. We also demonstrate the efficacy of the proposed technique in real-world applications by applying it to an ECG classification problem. The python code implementing the proposed classifier can be found in PyTransKit (https://github.com/rohdelab/PyTransKit).

Radon cumulative distribution transform subspace modeling for image classification

We present a new supervised image classification method for problems where the data at hand conform to certain deformation models applied to unknown prototypes or templates. The method makes use of the previously described Radon Cumulative Distribution Transform (R-CDT) for image data, whose mathematical properties are exploited to express the image data in a form that is more suitable for machine learning. While certain operations such as translation, scaling, and higher-order transformations are challenging to model in native image space, we show the R-CDT can capture some of these variations and thus render the associated image classification problems easier to solve. The method is simple to implement, non-iterative, has no hyper-parameters to tune, it is computationally efficient, and provides competitive accuracies to state-of-the-art neural networks for many types of classification problems, especially in a learning with few labels setting. Furthermore, we show improvements with respect to neural network-based methods in terms of computational efficiency (it can be implemented without the use of GPUs), number of training samples needed for training, as well as out-of-distribution generalization. The Python code for reproducing our results is available at https://github.com/rohdelab/rcdt_ns_classifier.