The Radon Signed Cumulative Distribution Transform and its applications in classification of Signed Images

Here we describe a new image representation technique based on the mathematics of transport and optimal transport. The method relies on the combination of the well-known Radon transform for images and a recent signal representation method called the Signed Cumulative Distribution Transform. The newly proposed method generalizes previous transport-related image representation methods to arbitrary functions (images), and thus can be used in more applications. We describe the new transform, and some of its mathematical properties and demonstrate its ability to partition image classes with real and simulated data. In comparison to existing transport transform methods, as well as deep learning-based classification methods, the new transform more accurately represents the information content of signed images, and thus can be used to obtain higher classification accuracies. The implementation of the proposed method in Python language is integrated as a part of the software package PyTransKit, available on Github.

Local Sliced-Wasserstein Feature Sets for Illumination-invariant Face Recognition

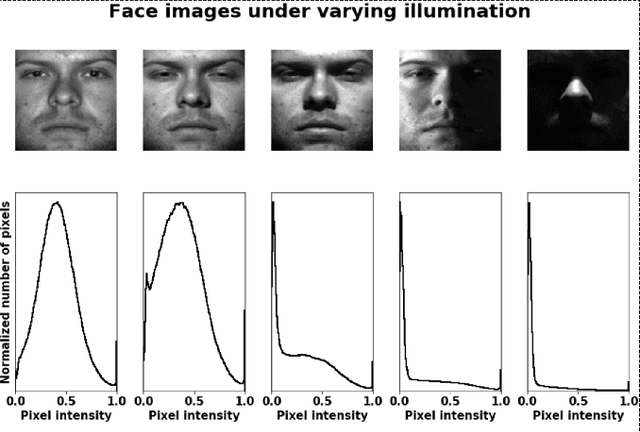
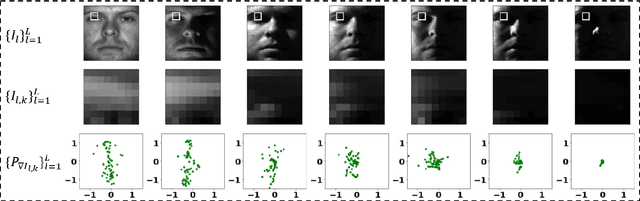
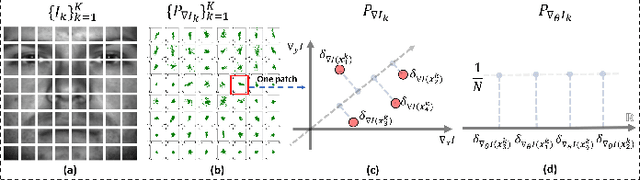
We present a new method for face recognition from digital images acquired under varying illumination conditions. The method is based on mathematical modeling of local gradient distributions using the Radon Cumulative Distribution Transform (R-CDT). We demonstrate that lighting variations cause certain types of deformations of local image gradient distributions which, when expressed in R-CDT domain, can be modeled as a subspace. Face recognition is then performed using a nearest subspace in R-CDT domain of local gradient distributions. Experiment results demonstrate the proposed method outperforms other alternatives in several face recognition tasks with challenging illumination conditions. Python code implementing the proposed method is available, which is integrated as a part of the software package PyTransKit.

Invariance encoding in sliced-Wasserstein space for image classification with limited training data

Deep convolutional neural networks (CNNs) are broadly considered to be state-of-the-art generic end-to-end image classification systems. However, they are known to underperform when training data are limited and thus require data augmentation strategies that render the method computationally expensive and not always effective. Rather than using a data augmentation strategy to encode invariances as typically done in machine learning, here we propose to mathematically augment a nearest subspace classification model in sliced-Wasserstein space by exploiting certain mathematical properties of the Radon Cumulative Distribution Transform (R-CDT), a recently introduced image transform. We demonstrate that for a particular type of learning problem, our mathematical solution has advantages over data augmentation with deep CNNs in terms of classification accuracy and computational complexity, and is particularly effective under a limited training data setting. The method is simple, effective, computationally efficient, non-iterative, and requires no parameters to be tuned. Python code implementing our method is available at https://github.com/rohdelab/mathematical_augmentation. Our method is integrated as a part of the software package PyTransKit, which is available at https://github.com/rohdelab/PyTransKit.

Nearest Subspace Search in The Signed Cumulative Distribution Transform Space for 1D Signal Classification

This paper presents a new method to classify 1D signals using the signed cumulative distribution transform (SCDT). The proposed method exploits certain linearization properties of the SCDT to render the problem easier to solve in the SCDT space. The method uses the nearest subspace search technique in the SCDT domain to provide a non-iterative, effective, and simple to implement classification algorithm. Experiments show that the proposed technique outperforms the state-of-the-art neural networks using a very low number of training samples and is also robust to out-of-distribution examples on simulated data. We also demonstrate the efficacy of the proposed technique in real-world applications by applying it to an ECG classification problem. The python code implementing the proposed classifier can be found in PyTransKit (https://github.com/rohdelab/PyTransKit).

Radon cumulative distribution transform subspace modeling for image classification

We present a new supervised image classification method for problems where the data at hand conform to certain deformation models applied to unknown prototypes or templates. The method makes use of the previously described Radon Cumulative Distribution Transform (R-CDT) for image data, whose mathematical properties are exploited to express the image data in a form that is more suitable for machine learning. While certain operations such as translation, scaling, and higher-order transformations are challenging to model in native image space, we show the R-CDT can capture some of these variations and thus render the associated image classification problems easier to solve. The method is simple to implement, non-iterative, has no hyper-parameters to tune, it is computationally efficient, and provides competitive accuracies to state-of-the-art neural networks for many types of classification problems, especially in a learning with few labels setting. Furthermore, we show improvements with respect to neural network-based methods in terms of computational efficiency (it can be implemented without the use of GPUs), number of training samples needed for training, as well as out-of-distribution generalization. The Python code for reproducing our results is available at https://github.com/rohdelab/rcdt_ns_classifier.