MARMOT: Masked Autoencoder for Modeling Transient Imaging

Pretrained models have demonstrated impressive success in many modalities such as language and vision. Recent works facilitate the pretraining paradigm in imaging research. Transients are a novel modality, which are captured for an object as photon counts versus arrival times using a precisely time-resolved sensor. In particular for non-line-of-sight (NLOS) scenarios, transients of hidden objects are measured beyond the sensor's direct line of sight. Using NLOS transients, the majority of previous works optimize volume density or surfaces to reconstruct the hidden objects and do not transfer priors learned from datasets. In this work, we present a masked autoencoder for modeling transient imaging, or MARMOT, to facilitate NLOS applications. Our MARMOT is a self-supervised model pretrianed on massive and diverse NLOS transient datasets. Using a Transformer-based encoder-decoder, MARMOT learns features from partially masked transients via a scanning pattern mask (SPM), where the unmasked subset is functionally equivalent to arbitrary sampling, and predicts full measurements. Pretrained on TransVerse-a synthesized transient dataset of 500K 3D models-MARMOT adapts to downstream imaging tasks using direct feature transfer or decoder finetuning. Comprehensive experiments are carried out in comparisons with state-of-the-art methods. Quantitative and qualitative results demonstrate the efficiency of our MARMOT.

VividListener: Expressive and Controllable Listener Dynamics Modeling for Multi-Modal Responsive Interaction

Generating responsive listener head dynamics with nuanced emotions and expressive reactions is crucial for practical dialogue modeling in various virtual avatar animations. Previous studies mainly focus on the direct short-term production of listener behavior. They overlook the fine-grained control over motion variations and emotional intensity, especially in long-sequence modeling. Moreover, the lack of long-term and large-scale paired speaker-listener corpora including head dynamics and fine-grained multi-modality annotations (e.g., text-based expression descriptions, emotional intensity) also limits the application of dialogue modeling.Therefore, we first newly collect a large-scale multi-turn dataset of 3D dyadic conversation containing more than 1.4M valid frames for multi-modal responsive interaction, dubbed ListenerX. Additionally, we propose VividListener, a novel framework enabling fine-grained, expressive and controllable listener dynamics modeling. This framework leverages multi-modal conditions as guiding principles for fostering coherent interactions between speakers and listeners.Specifically, we design the Responsive Interaction Module (RIM) to adaptively represent the multi-modal interactive embeddings. RIM ensures the listener dynamics achieve fine-grained semantic coordination with textual descriptions and adjustments, while preserving expressive reaction with speaker behavior. Meanwhile, we design the Emotional Intensity Tags (EIT) for emotion intensity editing with multi-modal information integration, applying to both text descriptions and listener motion amplitude.Extensive experiments conducted on our newly collected ListenerX dataset demonstrate that VividListener achieves state-of-the-art performance, realizing expressive and controllable listener dynamics.

TransiT: Transient Transformer for Non-line-of-sight Videography

High quality and high speed videography using Non-Line-of-Sight (NLOS) imaging benefit autonomous navigation, collision prevention, and post-disaster search and rescue tasks. Current solutions have to balance between the frame rate and image quality. High frame rates, for example, can be achieved by reducing either per-point scanning time or scanning density, but at the cost of lowering the information density at individual frames. Fast scanning process further reduces the signal-to-noise ratio and different scanning systems exhibit different distortion characteristics. In this work, we design and employ a new Transient Transformer architecture called TransiT to achieve real-time NLOS recovery under fast scans. TransiT directly compresses the temporal dimension of input transients to extract features, reducing computation costs and meeting high frame rate requirements. It further adopts a feature fusion mechanism as well as employs a spatial-temporal Transformer to help capture features of NLOS transient videos. Moreover, TransiT applies transfer learning to bridge the gap between synthetic and real-measured data. In real experiments, TransiT manages to reconstruct from sparse transients of $16 \times 16$ measured at an exposure time of 0.4 ms per point to NLOS videos at a $64 \times 64$ resolution at 10 frames per second. We will make our code and dataset available to the community.

Metric properties of partial and robust Gromov-Wasserstein distances

The Gromov-Wasserstein (GW) distances define a family of metrics, based on ideas from optimal transport, which enable comparisons between probability measures defined on distinct metric spaces. They are particularly useful in areas such as network analysis and geometry processing, as computation of a GW distance involves solving for registration between the objects which minimizes geometric distortion. Although GW distances have proven useful for various applications in the recent machine learning literature, it has been observed that they are inherently sensitive to outlier noise and cannot accommodate partial matching. This has been addressed by various constructions building on the GW framework; in this article, we focus specifically on a natural relaxation of the GW optimization problem, introduced by Chapel et al., which is aimed at addressing exactly these shortcomings. Our goal is to understand the theoretical properties of this relaxed optimization problem, from the viewpoint of metric geometry. While the relaxed problem fails to induce a metric, we derive precise characterizations of how it fails the axioms of non-degeneracy and triangle inequality. These observations lead us to define a novel family of distances, whose construction is inspired by the Prokhorov and Ky Fan distances, as well as by the recent work of Raghvendra et al.\ on robust versions of classical Wasserstein distance. We show that our new distances define true metrics, that they induce the same topology as the GW distances, and that they enjoy additional robustness to perturbations. These results provide a mathematically rigorous basis for using our robust partial GW distances in applications where outliers and partial matching are concerns.

SAM-OCTA2: Layer Sequence OCTA Segmentation with Fine-tuned Segment Anything Model 2

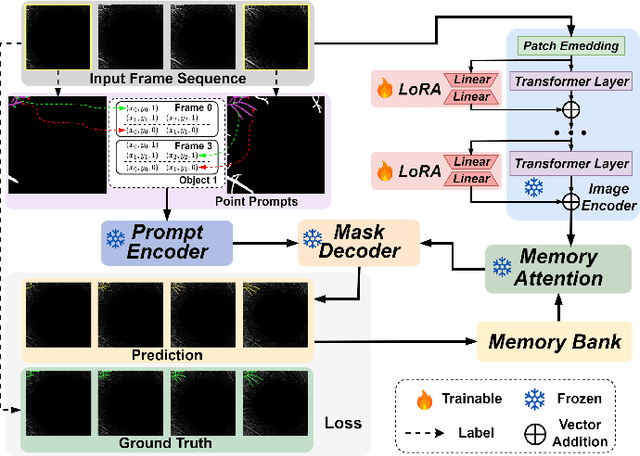
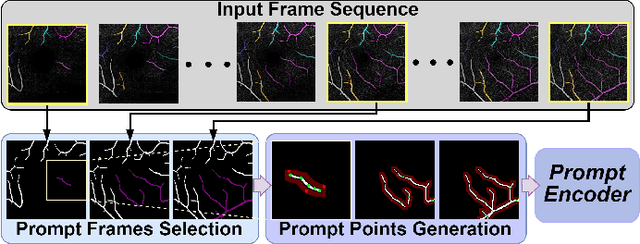
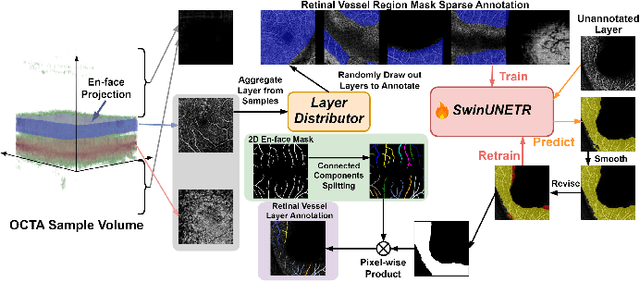
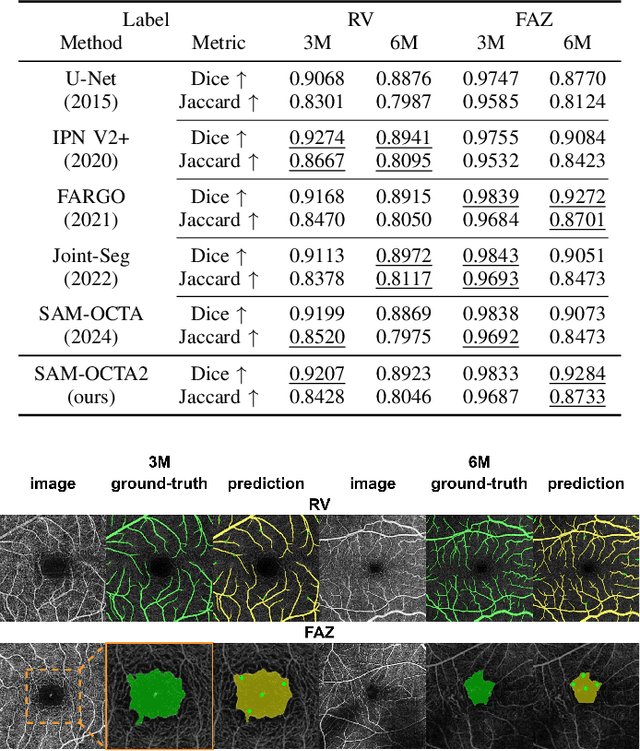
Segmentation of indicated targets aids in the precise analysis of optical coherence tomography angiography (OCTA) samples. Existing segmentation methods typically perform on 2D projection targets, making it challenging to capture the variance of segmented objects through the 3D volume. To address this limitation, the low-rank adaptation technique is adopted to fine-tune the Segment Anything Model (SAM) version 2, enabling the tracking and segmentation of specified objects across the OCTA scanning layer sequence. To further this work, a prompt point generation strategy in frame sequence and a sparse annotation method to acquire retinal vessel (RV) layer masks are proposed. This method is named SAM-OCTA2 and has been experimented on the OCTA-500 dataset. It achieves state-of-the-art performance in segmenting the foveal avascular zone (FAZ) on regular 2D en-face and effectively tracks local vessels across scanning layer sequences. The code is available at: https://github.com/ShellRedia/SAM-OCTA2.

Snake with Shifted Window: Learning to Adapt Vessel Pattern for OCTA Segmentation

Segmenting specific targets or structures in optical coherence tomography angiography (OCTA) images is fundamental for conducting further pathological studies. The retinal vascular layers are rich and intricate, and such vascular with complex shapes can be captured by the widely-studied OCTA images. In this paper, we thus study how to use OCTA images with projection vascular layers to segment retinal structures. To this end, we propose the SSW-OCTA model, which integrates the advantages of deformable convolutions suited for tubular structures and the swin-transformer for global feature extraction, adapting to the characteristics of OCTA modality images. Our model underwent testing and comparison on the OCTA-500 dataset, achieving state-of-the-art performance. The code is available at: https://github.com/ShellRedia/Snake-SWin-OCTA.

Linear optimal transport subspaces for point set classification

Learning from point sets is an essential component in many computer vision and machine learning applications. Native, unordered, and permutation invariant set structure space is challenging to model, particularly for point set classification under spatial deformations. Here we propose a framework for classifying point sets experiencing certain types of spatial deformations, with a particular emphasis on datasets featuring affine deformations. Our approach employs the Linear Optimal Transport (LOT) transform to obtain a linear embedding of set-structured data. Utilizing the mathematical properties of the LOT transform, we demonstrate its capacity to accommodate variations in point sets by constructing a convex data space, effectively simplifying point set classification problems. Our method, which employs a nearest-subspace algorithm in the LOT space, demonstrates label efficiency, non-iterative behavior, and requires no hyper-parameter tuning. It achieves competitive accuracies compared to state-of-the-art methods across various point set classification tasks. Furthermore, our approach exhibits robustness in out-of-distribution scenarios where training and test distributions vary in terms of deformation magnitudes.

Visual Decoding and Reconstruction via EEG Embeddings with Guided Diffusion

How to decode human vision through neural signals has attracted a long-standing interest in neuroscience and machine learning. Modern contrastive learning and generative models improved the performance of fMRI-based visual decoding and reconstruction. However, the high cost and low temporal resolution of fMRI limit their applications in brain-computer interfaces (BCIs), prompting a high need for EEG-based visual reconstruction. In this study, we present an EEG-based visual reconstruction framework. It consists of a plug-and-play EEG encoder called the Adaptive Thinking Mapper (ATM), which is aligned with image embeddings, and a two-stage EEG guidance image generator that first transforms EEG features into image priors and then reconstructs the visual stimuli with a pre-trained image generator. Our approach allows EEG embeddings to achieve superior performance in image classification and retrieval tasks. Our two-stage image generation strategy vividly reconstructs images seen by humans. Furthermore, we analyzed the impact of signals from different time windows and brain regions on decoding and reconstruction. The versatility of our framework is demonstrated in the magnetoencephalogram (MEG) data modality. We report that EEG-based visual decoding achieves SOTA performance, highlighting the portability, low cost, and high temporal resolution of EEG, enabling a wide range of BCI applications. The code of ATM is available at https://github.com/dongyangli-del/EEG_Image_decode.

Approximation properties of slice-matching operators

Iterative slice-matching procedures are efficient schemes for transferring a source measure to a target measure, especially in high dimensions. These schemes have been successfully used in applications such as color transfer and shape retrieval, and are guaranteed to converge under regularity assumptions. In this paper, we explore approximation properties related to a single step of such iterative schemes by examining an associated slice-matching operator, depending on a source measure, a target measure, and slicing directions. In particular, we demonstrate an invariance property with respect to the source measure, an equivariance property with respect to the target measure, and Lipschitz continuity concerning the slicing directions. We furthermore establish error bounds corresponding to approximating the target measure by one step of the slice-matching scheme and characterize situations in which the slice-matching operator recovers the optimal transport map between two measures. We also investigate connections to affine registration problems with respect to (sliced) Wasserstein distances. These connections can be also be viewed as extensions to the invariance and equivariance properties of the slice-matching operator and illustrate the extent to which slice-matching schemes incorporate affine effects.

SAM-OCTA: Prompting Segment-Anything for OCTA Image Segmentation

In the analysis of optical coherence tomography angiography (OCTA) images, the operation of segmenting specific targets is necessary. Existing methods typically train on supervised datasets with limited samples (approximately a few hundred), which can lead to overfitting. To address this, the low-rank adaptation technique is adopted for foundation model fine-tuning and proposed corresponding prompt point generation strategies to process various segmentation tasks on OCTA datasets. This method is named SAM-OCTA and has been experimented on the publicly available OCTA-500 and ROSE datasets. This method achieves or approaches state-of-the-art segmentation performance metrics. The effect and applicability of prompt points are discussed in detail for the retinal vessel, foveal avascular zone, capillary, artery, and vein segmentation tasks. Furthermore, SAM-OCTA accomplishes local vessel segmentation and effective artery-vein segmentation, which was not well-solved in previous works. The code is available at https://github.com/ShellRedia/SAM-OCTA.