The Radon Signed Cumulative Distribution Transform and its applications in classification of Signed Images

Here we describe a new image representation technique based on the mathematics of transport and optimal transport. The method relies on the combination of the well-known Radon transform for images and a recent signal representation method called the Signed Cumulative Distribution Transform. The newly proposed method generalizes previous transport-related image representation methods to arbitrary functions (images), and thus can be used in more applications. We describe the new transform, and some of its mathematical properties and demonstrate its ability to partition image classes with real and simulated data. In comparison to existing transport transform methods, as well as deep learning-based classification methods, the new transform more accurately represents the information content of signed images, and thus can be used to obtain higher classification accuracies. The implementation of the proposed method in Python language is integrated as a part of the software package PyTransKit, available on Github.

Signed Cumulative Distribution Transform for Parameter Estimation of 1-D Signals

We describe a method for signal parameter estimation using the signed cumulative distribution transform (SCDT), a recently introduced signal representation tool based on optimal transport theory. The method builds upon signal estimation using the cumulative distribution transform (CDT) originally introduced for positive distributions. Specifically, we show that Wasserstein-type distance minimization can be performed simply using linear least squares techniques in SCDT space for arbitrary signal classes, thus providing a global minimizer for the estimation problem even when the underlying signal is a nonlinear function of the unknown parameters. Comparisons to current signal estimation methods using $L_p$ minimization shows the advantage of the method.

The Signed Cumulative Distribution Transform for 1-D Signal Analysis and Classification

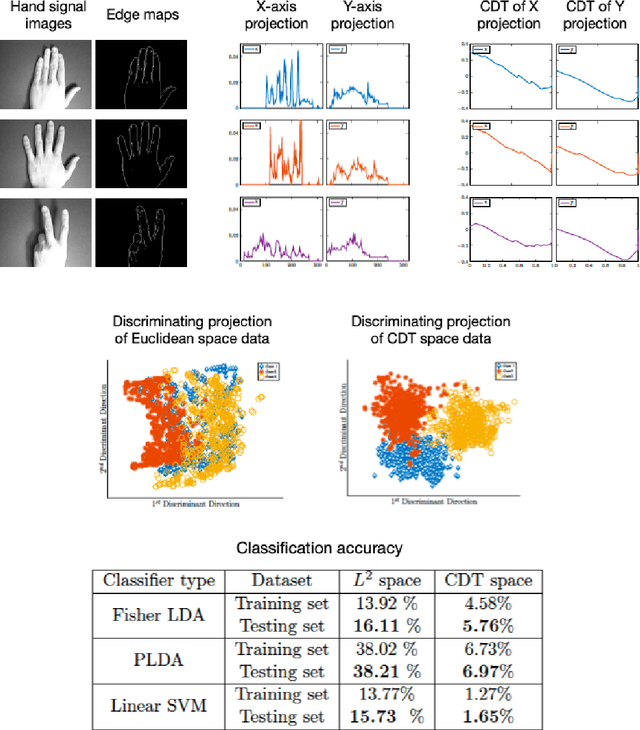
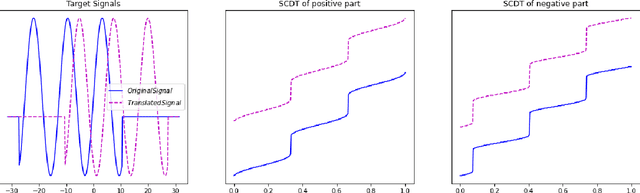
This paper presents a new mathematical signal transform that is especially suitable for decoding information related to non-rigid signal displacements. We provide a measure theoretic framework to extend the existing Cumulative Distribution Transform [ACHA 45 (2018), no. 3, 616-641] to arbitrary (signed) signals on $\overline{\mathbb{R}}$. We present both forward (analysis) and inverse (synthesis) formulas for the transform, and describe several of its properties including translation, scaling, convexity, linear separability and others. Finally, we describe a metric in transform space, and demonstrate the application of the transform in classifying (detecting) signals under random displacements.