Signed Cumulative Distribution Transform for Parameter Estimation of 1-D Signals

We describe a method for signal parameter estimation using the signed cumulative distribution transform (SCDT), a recently introduced signal representation tool based on optimal transport theory. The method builds upon signal estimation using the cumulative distribution transform (CDT) originally introduced for positive distributions. Specifically, we show that Wasserstein-type distance minimization can be performed simply using linear least squares techniques in SCDT space for arbitrary signal classes, thus providing a global minimizer for the estimation problem even when the underlying signal is a nonlinear function of the unknown parameters. Comparisons to current signal estimation methods using $L_p$ minimization shows the advantage of the method.

The Cumulative Distribution Transform and Linear Pattern Classification

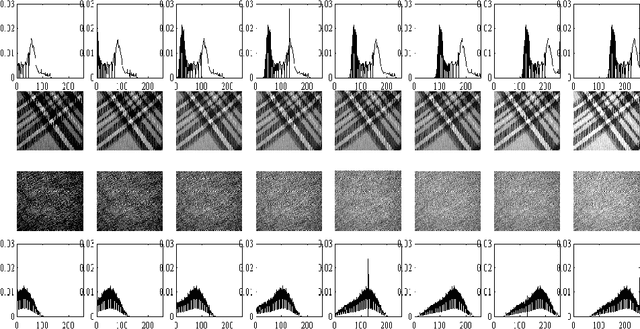
Discriminating data classes emanating from sensors is an important problem with many applications in science and technology. We describe a new transform for pattern identification that interprets patterns as probability density functions, and has special properties with regards to classification. The transform, which we denote as the Cumulative Distribution Transform (CDT) is invertible, with well defined forward and inverse operations. We show that it can be useful in `parsing out' variations (confounds) that are `Lagrangian' (displacement and intensity variations) by converting these to `Eulerian' (intensity variations) in transform space. This conversion is the basis for our main result that describes when the CDT can allow for linear classification to be possible in transform space. We also describe several properties of the transform and show, with computational experiments that used both real and simulated data, that the CDT can help render a variety of real world problems simpler to solve.