The Cumulative Distribution Transform and Linear Pattern Classification

Discriminating data classes emanating from sensors is an important problem with many applications in science and technology. We describe a new transform for pattern identification that interprets patterns as probability density functions, and has special properties with regards to classification. The transform, which we denote as the Cumulative Distribution Transform (CDT) is invertible, with well defined forward and inverse operations. We show that it can be useful in `parsing out' variations (confounds) that are `Lagrangian' (displacement and intensity variations) by converting these to `Eulerian' (intensity variations) in transform space. This conversion is the basis for our main result that describes when the CDT can allow for linear classification to be possible in transform space. We also describe several properties of the transform and show, with computational experiments that used both real and simulated data, that the CDT can help render a variety of real world problems simpler to solve.

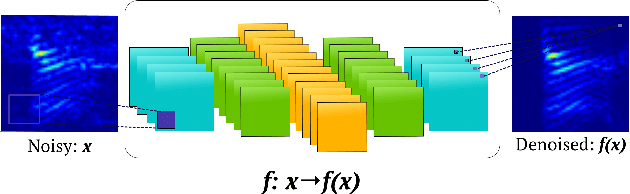
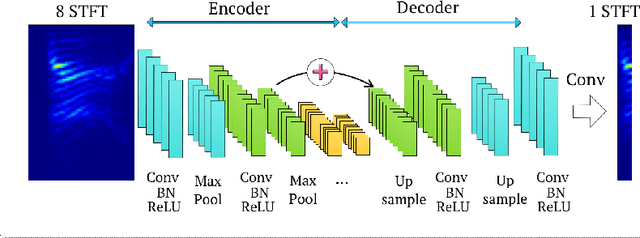
A Fully Convolutional Neural Network for Speech Enhancement

In hearing aids, the presence of babble noise degrades hearing intelligibility of human speech greatly. However, removing the babble without creating artifacts in human speech is a challenging task in a low SNR environment. Here, we sought to solve the problem by finding a `mapping' between noisy speech spectra and clean speech spectra via supervised learning. Specifically, we propose using fully Convolutional Neural Networks, which consist of lesser number of parameters than fully connected networks. The proposed network, Redundant Convolutional Encoder Decoder (R-CED), demonstrates that a convolutional network can be 12 times smaller than a recurrent network and yet achieves better performance, which shows its applicability for an embedded system: the hearing aids.

The Radon cumulative distribution transform and its application to image classification

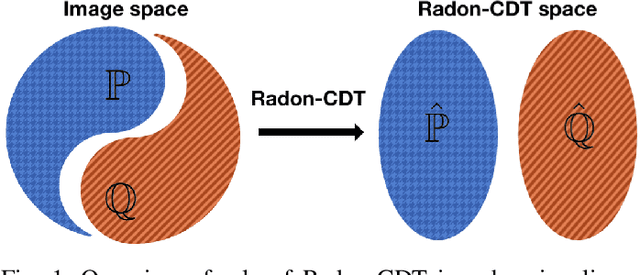
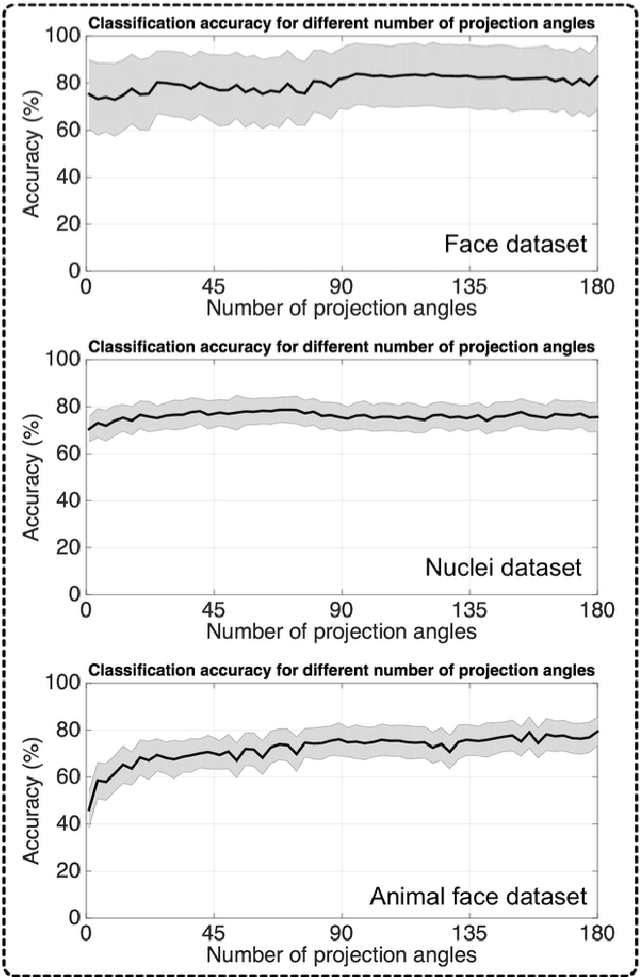
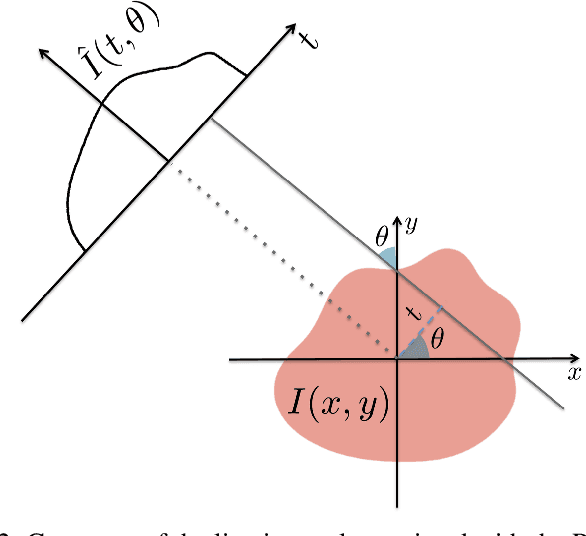
Invertible image representation methods (transforms) are routinely employed as low-level image processing operations based on which feature extraction and recognition algorithms are developed. Most transforms in current use (e.g. Fourier, Wavelet, etc.) are linear transforms, and, by themselves, are unable to substantially simplify the representation of image classes for classification. Here we describe a nonlinear, invertible, low-level image processing transform based on combining the well known Radon transform for image data, and the 1D Cumulative Distribution Transform proposed earlier. We describe a few of the properties of this new transform, and with both theoretical and experimental results show that it can often render certain problems linearly separable in transform space.