Discovery and visualization of structural biomarkers from MRI using transport-based morphometry

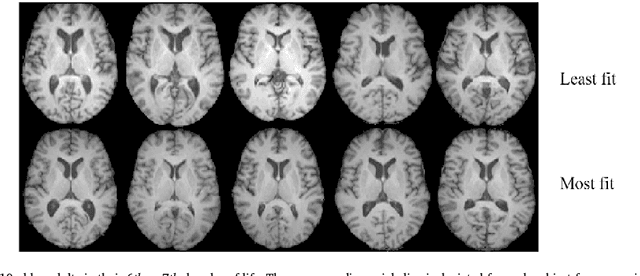
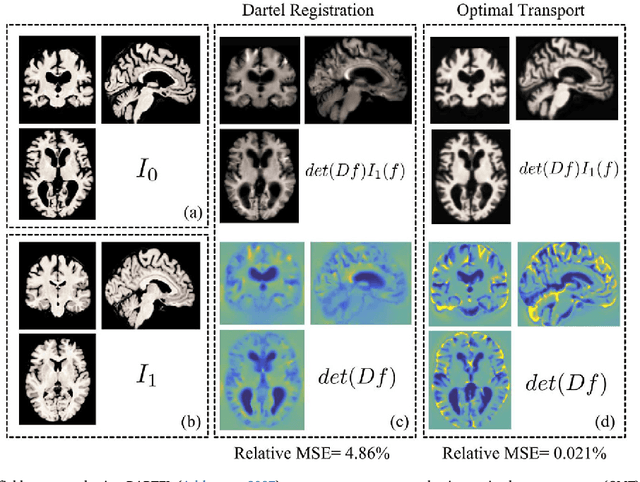
Disease in the brain is often associated with subtle, spatially diffuse, or complex tissue changes that may lie beneath the level of gross visual inspection, even on magnetic resonance imaging (MRI). Unfortunately, current computer-assisted approaches that examine pre-specified features, whether anatomically-defined (i.e. thalamic volume, cortical thickness) or based on pixelwise comparison (i.e. deformation-based methods), are prone to missing a vast array of physical changes that are not well-encapsulated by these metrics. In this paper, we have developed a technique for automated pattern analysis that can fully determine the relationship between brain structure and observable phenotype without requiring any a priori features. Our technique, called transport-based morphometry (TBM), is an image transformation that maps brain images losslessly to a domain where they become much more separable. The new approach is validated on structural brain images of healthy older adult subjects where even linear models for discrimination, regression, and blind source separation enable TBM to independently discover the characteristic changes of aging and highlight potential mechanisms by which aerobic fitness may mediate brain health later in life. TBM is a generative approach that can provide visualization of physically meaningful shifts in tissue distribution through inverse transformation. The proposed framework is a powerful technique that can potentially elucidate genotype-structural-behavioral associations in myriad diseases.

The Cumulative Distribution Transform and Linear Pattern Classification

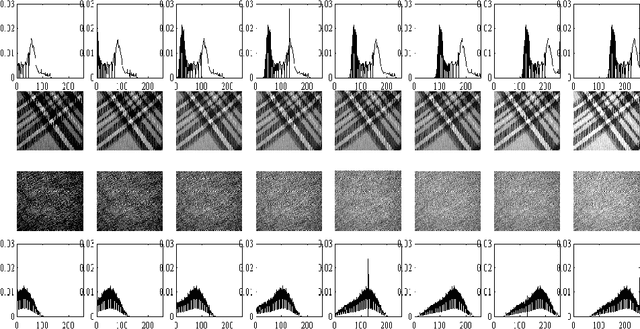
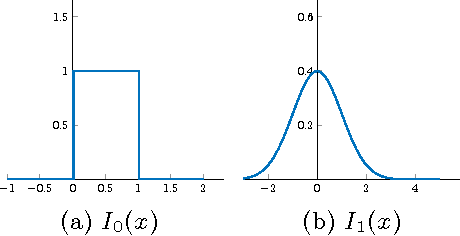
Discriminating data classes emanating from sensors is an important problem with many applications in science and technology. We describe a new transform for pattern identification that interprets patterns as probability density functions, and has special properties with regards to classification. The transform, which we denote as the Cumulative Distribution Transform (CDT) is invertible, with well defined forward and inverse operations. We show that it can be useful in `parsing out' variations (confounds) that are `Lagrangian' (displacement and intensity variations) by converting these to `Eulerian' (intensity variations) in transform space. This conversion is the basis for our main result that describes when the CDT can allow for linear classification to be possible in transform space. We also describe several properties of the transform and show, with computational experiments that used both real and simulated data, that the CDT can help render a variety of real world problems simpler to solve.