An Efficient Transport-Based Dissimilarity Measure for Time Series Classification under Warping Distortions

Time Series Classification (TSC) is an important problem with numerous applications in science and technology. Dissimilarity-based approaches, such as Dynamic Time Warping (DTW), are classical methods for distinguishing time series when time deformations are confounding information. In this paper, starting from a deformation-based model for signal classes we define a problem statement for time series classification problem. We show that, under theoretically ideal conditions, a continuous version of classic 1NN-DTW method can solve the stated problem, even when only one training sample is available. In addition, we propose an alternative dissimilarity measure based on Optimal Transport and show that it can also solve the aforementioned problem statement at a significantly reduced computational cost. Finally, we demonstrate the application of the newly proposed approach in simulated and real time series classification data, showing the efficacy of the method.

LCOT: Linear circular optimal transport

The optimal transport problem for measures supported on non-Euclidean spaces has recently gained ample interest in diverse applications involving representation learning. In this paper, we focus on circular probability measures, i.e., probability measures supported on the unit circle, and introduce a new computationally efficient metric for these measures, denoted as Linear Circular Optimal Transport (LCOT). The proposed metric comes with an explicit linear embedding that allows one to apply Machine Learning (ML) algorithms to the embedded measures and seamlessly modify the underlying metric for the ML algorithm to LCOT. We show that the proposed metric is rooted in the Circular Optimal Transport (COT) and can be considered the linearization of the COT metric with respect to a fixed reference measure. We provide a theoretical analysis of the proposed metric and derive the computational complexities for pairwise comparison of circular probability measures. Lastly, through a set of numerical experiments, we demonstrate the benefits of LCOT in learning representations of circular measures.

Linear Optimal Partial Transport Embedding

Optimal transport (OT) has gained popularity due to its various applications in fields such as machine learning, statistics, and signal processing. However, the balanced mass requirement limits its performance in practical problems. To address these limitations, variants of the OT problem, including unbalanced OT, Optimal partial transport (OPT), and Hellinger Kantorovich (HK), have been proposed. In this paper, we propose the Linear optimal partial transport (LOPT) embedding, which extends the (local) linearization technique on OT and HK to the OPT problem. The proposed embedding allows for faster computation of OPT distance between pairs of positive measures. Besides our theoretical contributions, we demonstrate the LOPT embedding technique in point-cloud interpolation and PCA analysis.

Signed Cumulative Distribution Transform for Parameter Estimation of 1-D Signals

We describe a method for signal parameter estimation using the signed cumulative distribution transform (SCDT), a recently introduced signal representation tool based on optimal transport theory. The method builds upon signal estimation using the cumulative distribution transform (CDT) originally introduced for positive distributions. Specifically, we show that Wasserstein-type distance minimization can be performed simply using linear least squares techniques in SCDT space for arbitrary signal classes, thus providing a global minimizer for the estimation problem even when the underlying signal is a nonlinear function of the unknown parameters. Comparisons to current signal estimation methods using $L_p$ minimization shows the advantage of the method.

The Signed Cumulative Distribution Transform for 1-D Signal Analysis and Classification

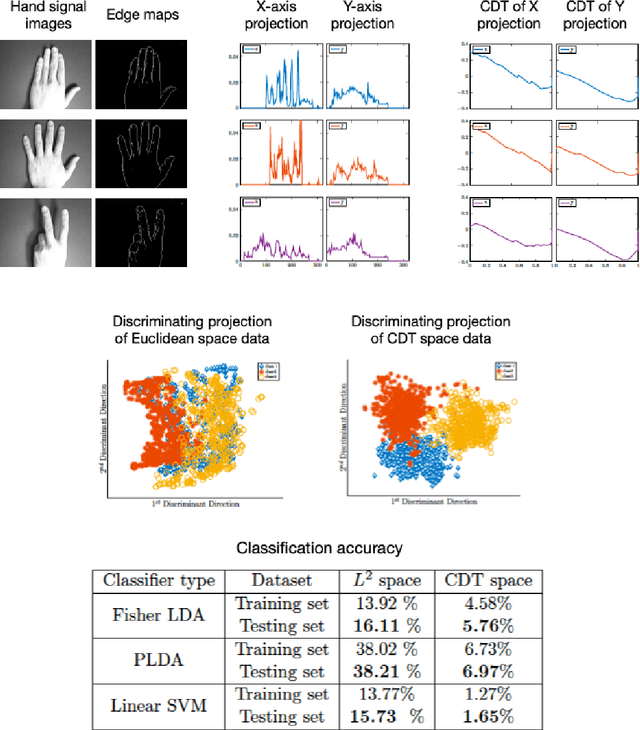
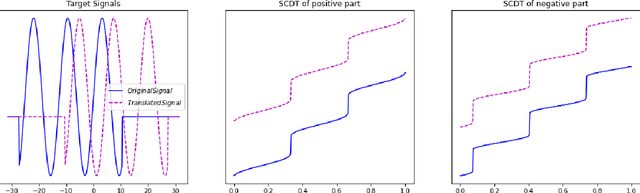
This paper presents a new mathematical signal transform that is especially suitable for decoding information related to non-rigid signal displacements. We provide a measure theoretic framework to extend the existing Cumulative Distribution Transform [ACHA 45 (2018), no. 3, 616-641] to arbitrary (signed) signals on $\overline{\mathbb{R}}$. We present both forward (analysis) and inverse (synthesis) formulas for the transform, and describe several of its properties including translation, scaling, convexity, linear separability and others. Finally, we describe a metric in transform space, and demonstrate the application of the transform in classifying (detecting) signals under random displacements.