Optimal lower bounds for logistic log-likelihoods

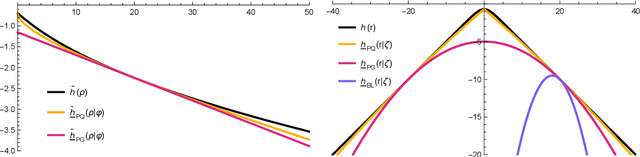
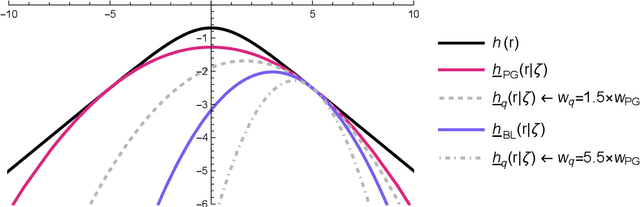
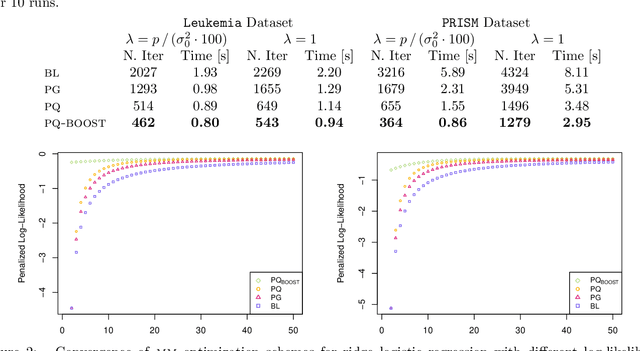
The logit transform is arguably the most widely-employed link function beyond linear settings. This transformation routinely appears in regression models for binary data and provides, either explicitly or implicitly, a core building-block within state-of-the-art methodologies for both classification and regression. Its widespread use, combined with the lack of analytical solutions for the optimization of general losses involving the logit transform, still motivates active research in computational statistics. Among the directions explored, a central one has focused on the design of tangent lower bounds for logistic log-likelihoods that can be tractably optimized, while providing a tight approximation of these log-likelihoods. Although progress along these lines has led to the development of effective minorize-maximize (MM) algorithms for point estimation and coordinate ascent variational inference schemes for approximate Bayesian inference under several logit models, the overarching focus in the literature has been on tangent quadratic minorizers. In fact, it is still unclear whether tangent lower bounds sharper than quadratic ones can be derived without undermining the tractability of the resulting minorizer. This article addresses such a challenging question through the design and study of a novel piece-wise quadratic lower bound that uniformly improves any tangent quadratic minorizer, including the sharpest ones, while admitting a direct interpretation in terms of the classical generalized lasso problem. As illustrated in a ridge logistic regression, this unique connection facilitates more effective implementations than those provided by available piece-wise bounds, while improving the convergence speed of quadratic ones.

Efficient expectation propagation for posterior approximation in high-dimensional probit models

Bayesian binary regression is a prosperous area of research due to the computational challenges encountered by currently available methods either for high-dimensional settings or large datasets, or both. In the present work, we focus on the expectation propagation (EP) approximation of the posterior distribution in Bayesian probit regression under a multivariate Gaussian prior distribution. Adapting more general derivations in Anceschi et al. (2023), we show how to leverage results on the extended multivariate skew-normal distribution to derive an efficient implementation of the EP routine having a per-iteration cost that scales linearly in the number of covariates. This makes EP computationally feasible also in challenging high-dimensional settings, as shown in a detailed simulation study.

Expectation propagation for the smoothing distribution in dynamic probit

The smoothing distribution of dynamic probit models with Gaussian state dynamics was recently proved to belong to the unified skew-normal family. Although this is computationally tractable in small-to-moderate settings, it may become computationally impractical in higher dimensions. In this work, adapting a recent more general class of expectation propagation (EP) algorithms, we derive an efficient EP routine to perform inference for such a distribution. We show that the proposed approximation leads to accuracy gains over available approximate algorithms in a financial illustration.

Efficient computation of predictive probabilities in probit models via expectation propagation

Binary regression models represent a popular model-based approach for binary classification. In the Bayesian framework, computational challenges in the form of the posterior distribution motivate still-ongoing fruitful research. Here, we focus on the computation of predictive probabilities in Bayesian probit models via expectation propagation (EP). Leveraging more general results in recent literature, we show that such predictive probabilities admit a closed-form expression. Improvements over state-of-the-art approaches are shown in a simulation study.

Bayesian Inference for the Multinomial Probit Model under Gaussian Prior Distribution

Multinomial probit (mnp) models are fundamental and widely-applied regression models for categorical data. Fasano and Durante (2022) proved that the class of unified skew-normal distributions is conjugate to several mnp sampling models. This allows to develop Monte Carlo samplers and accurate variational methods to perform Bayesian inference. In this paper, we adapt the abovementioned results for a popular special case: the discrete-choice mnp model under zero mean and independent Gaussian priors. This allows to obtain simplified expressions for the parameters of the posterior distribution and an alternative derivation for the variational algorithm that gives a novel understanding of the fundamental results in Fasano and Durante (2022) as well as computational advantages in our special settings.