Efficient expectation propagation for posterior approximation in high-dimensional probit models

Bayesian binary regression is a prosperous area of research due to the computational challenges encountered by currently available methods either for high-dimensional settings or large datasets, or both. In the present work, we focus on the expectation propagation (EP) approximation of the posterior distribution in Bayesian probit regression under a multivariate Gaussian prior distribution. Adapting more general derivations in Anceschi et al. (2023), we show how to leverage results on the extended multivariate skew-normal distribution to derive an efficient implementation of the EP routine having a per-iteration cost that scales linearly in the number of covariates. This makes EP computationally feasible also in challenging high-dimensional settings, as shown in a detailed simulation study.

Expectation propagation for the smoothing distribution in dynamic probit

The smoothing distribution of dynamic probit models with Gaussian state dynamics was recently proved to belong to the unified skew-normal family. Although this is computationally tractable in small-to-moderate settings, it may become computationally impractical in higher dimensions. In this work, adapting a recent more general class of expectation propagation (EP) algorithms, we derive an efficient EP routine to perform inference for such a distribution. We show that the proposed approximation leads to accuracy gains over available approximate algorithms in a financial illustration.

Efficient computation of predictive probabilities in probit models via expectation propagation

Binary regression models represent a popular model-based approach for binary classification. In the Bayesian framework, computational challenges in the form of the posterior distribution motivate still-ongoing fruitful research. Here, we focus on the computation of predictive probabilities in Bayesian probit models via expectation propagation (EP). Leveraging more general results in recent literature, we show that such predictive probabilities admit a closed-form expression. Improvements over state-of-the-art approaches are shown in a simulation study.

Bayesian Inference for the Multinomial Probit Model under Gaussian Prior Distribution

Multinomial probit (mnp) models are fundamental and widely-applied regression models for categorical data. Fasano and Durante (2022) proved that the class of unified skew-normal distributions is conjugate to several mnp sampling models. This allows to develop Monte Carlo samplers and accurate variational methods to perform Bayesian inference. In this paper, we adapt the abovementioned results for a popular special case: the discrete-choice mnp model under zero mean and independent Gaussian priors. This allows to obtain simplified expressions for the parameters of the posterior distribution and an alternative derivation for the variational algorithm that gives a novel understanding of the fundamental results in Fasano and Durante (2022) as well as computational advantages in our special settings.

A Class of Conjugate Priors for Multinomial Probit Models which Includes the Multivariate Normal One

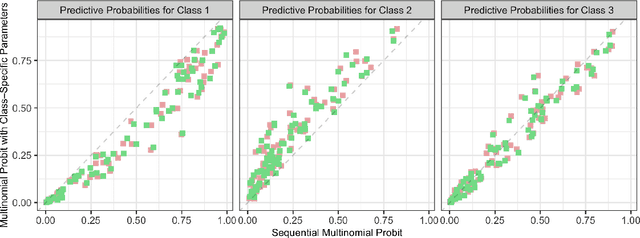
Multinomial probit models are widely-implemented representations which allow both classification and inference by learning changes in vectors of class probabilities with a set of p observed predictors. Although various frequentist methods have been developed for estimation, inference and classification within such a class of models, Bayesian inference is still lagging behind. This is due to the apparent absence of a tractable class of conjugate priors, that may facilitate posterior inference on the multinomial probit coefficients. Such an issue has motivated increasing efforts toward the development of effective Markov chain Monte Carlo methods, but state-of-the-art solutions still face severe computational bottlenecks, especially in large p settings. In this article, we prove that the entire class of unified skew-normal (SUN) distributions is conjugate to a wide variety of multinomial probit models, and we exploit the SUN properties to improve upon state-of-art-solutions for posterior inference and classification both in terms of closed-form results for key functionals of interest, and also by developing novel computational methods relying either on independent and identically distributed samples from the exact posterior or on scalable and accurate variational approximations based on blocked partially-factorized representations. As illustrated in a gastrointestinal lesions application, the magnitude of the improvements relative to current methods is particularly evident, in practice, when the focus is on large p applications.