Optimal lower bounds for logistic log-likelihoods

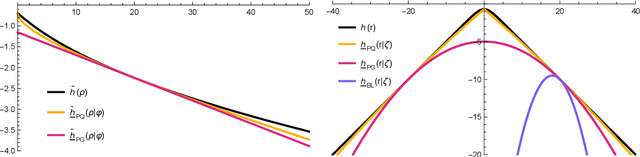
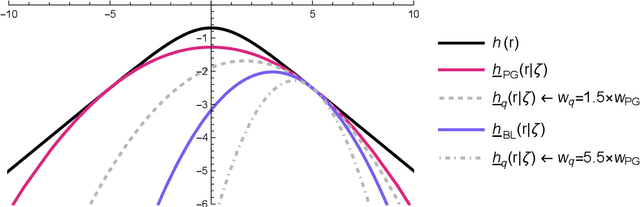
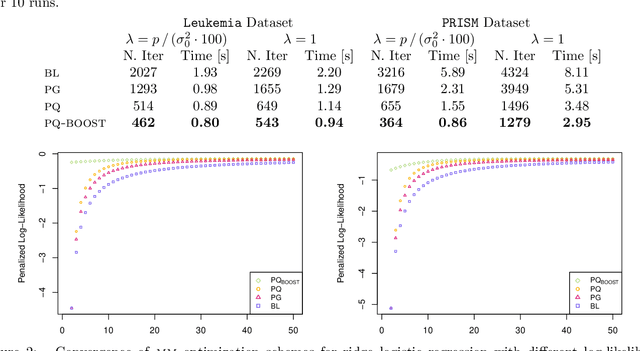
The logit transform is arguably the most widely-employed link function beyond linear settings. This transformation routinely appears in regression models for binary data and provides, either explicitly or implicitly, a core building-block within state-of-the-art methodologies for both classification and regression. Its widespread use, combined with the lack of analytical solutions for the optimization of general losses involving the logit transform, still motivates active research in computational statistics. Among the directions explored, a central one has focused on the design of tangent lower bounds for logistic log-likelihoods that can be tractably optimized, while providing a tight approximation of these log-likelihoods. Although progress along these lines has led to the development of effective minorize-maximize (MM) algorithms for point estimation and coordinate ascent variational inference schemes for approximate Bayesian inference under several logit models, the overarching focus in the literature has been on tangent quadratic minorizers. In fact, it is still unclear whether tangent lower bounds sharper than quadratic ones can be derived without undermining the tractability of the resulting minorizer. This article addresses such a challenging question through the design and study of a novel piece-wise quadratic lower bound that uniformly improves any tangent quadratic minorizer, including the sharpest ones, while admitting a direct interpretation in terms of the classical generalized lasso problem. As illustrated in a ridge logistic regression, this unique connection facilitates more effective implementations than those provided by available piece-wise bounds, while improving the convergence speed of quadratic ones.

Extended Stochastic Block Models

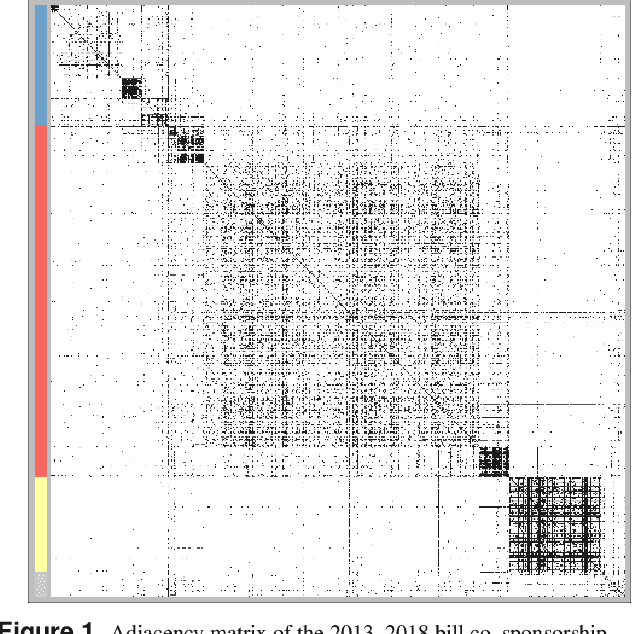
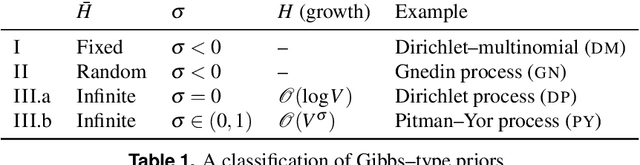
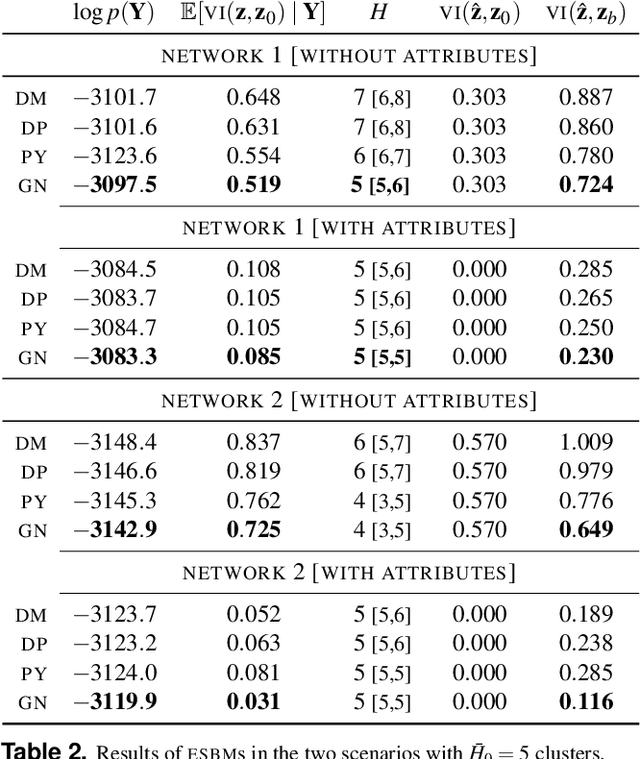
Stochastic block models (SBM) are widely used in network science due to their interpretable structure that allows inference on groups of nodes having common connectivity patterns. Although providing a well established model-based approach for community detection, such formulations are still the object of intense research to address the key problem of inferring the unknown number of communities. This has motivated the development of several probabilistic mechanisms to characterize the node partition process, covering solutions with fixed, random and infinite number of communities. In this article we provide a unified view of all these formulations within a single extended stochastic block model (ESBM), that relies on Gibbs-type processes and encompasses most existing representations as special cases. Connections with Bayesian nonparametric literature open up new avenues that allow the natural inclusion of several unexplored options to model the nodes partition process and to incorporate node attributes in a principled manner. Among these new alternatives, we focus on the Gnedin process as an example of a probabilistic mechanism with desirable theoretical properties and nice empirical performance. A collapsed Gibbs sampler that can be applied to the whole ESBM class is proposed, and refined methods for estimation, uncertainty quantification and model assessment are outlined. The performance of ESBM is assessed in simulations and an application to bill co-sponsorship networks in the Italian parliament, where we find key hidden block structures and core-periphery patterns.

A Class of Conjugate Priors for Multinomial Probit Models which Includes the Multivariate Normal One

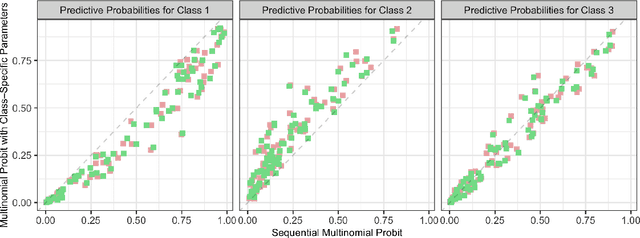
Multinomial probit models are widely-implemented representations which allow both classification and inference by learning changes in vectors of class probabilities with a set of p observed predictors. Although various frequentist methods have been developed for estimation, inference and classification within such a class of models, Bayesian inference is still lagging behind. This is due to the apparent absence of a tractable class of conjugate priors, that may facilitate posterior inference on the multinomial probit coefficients. Such an issue has motivated increasing efforts toward the development of effective Markov chain Monte Carlo methods, but state-of-the-art solutions still face severe computational bottlenecks, especially in large p settings. In this article, we prove that the entire class of unified skew-normal (SUN) distributions is conjugate to a wide variety of multinomial probit models, and we exploit the SUN properties to improve upon state-of-art-solutions for posterior inference and classification both in terms of closed-form results for key functionals of interest, and also by developing novel computational methods relying either on independent and identically distributed samples from the exact posterior or on scalable and accurate variational approximations based on blocked partially-factorized representations. As illustrated in a gastrointestinal lesions application, the magnitude of the improvements relative to current methods is particularly evident, in practice, when the focus is on large p applications.

Bayesian Learning of Dynamic Multilayer Networks

A plethora of networks is being collected in a growing number of fields, including disease transmission, international relations, social interactions, and others. As data streams continue to grow, the complexity associated with these highly multidimensional connectivity data presents novel challenges. In this paper, we focus on the time-varying interconnections among a set of actors in multiple contexts, called layers. Current literature lacks flexible statistical models for dynamic multilayer networks, which can enhance quality in inference and prediction by efficiently borrowing information within each network, across time, and between layers. Motivated by this gap, we develop a Bayesian nonparametric model leveraging latent space representations. Our formulation characterizes the edge probabilities as a function of shared and layer-specific actors positions in a latent space, with these positions changing in time via Gaussian processes. This representation facilitates dimensionality reduction and incorporates different sources of information in the observed data. In addition, we obtain tractable procedures for posterior computation, inference, and prediction. We provide theoretical results on the flexibility of our model. Our methods are tested on simulations and infection studies monitoring dynamic face-to-face contacts among individuals in multiple days, where we perform better than current methods in inference and prediction.

Locally Adaptive Dynamic Networks

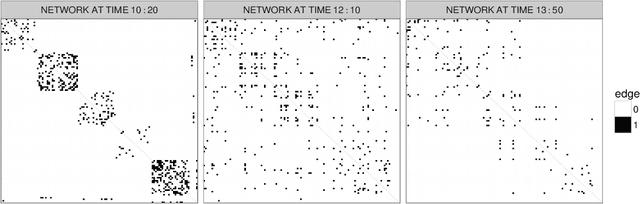
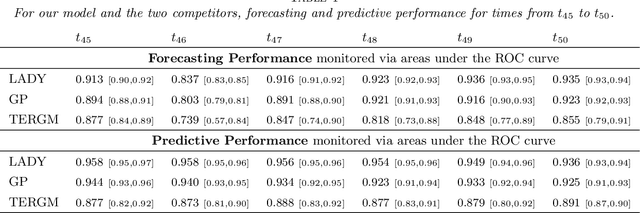
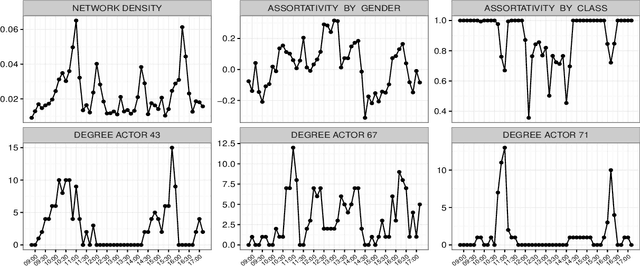
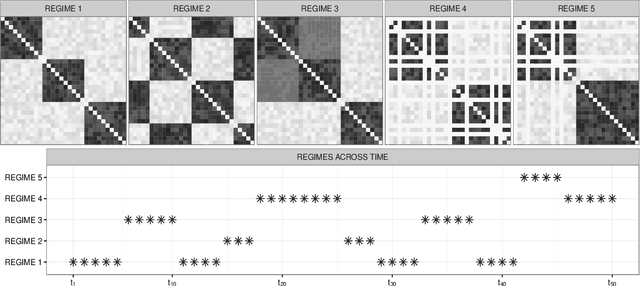
Our focus is on realistically modeling and forecasting dynamic networks of face-to-face contacts among individuals. Important aspects of such data that lead to problems with current methods include the tendency of the contacts to move between periods of slow and rapid changes, and the dynamic heterogeneity in the actors' connectivity behaviors. Motivated by this application, we develop a novel method for Locally Adaptive DYnamic (LADY) network inference. The proposed model relies on a dynamic latent space representation in which each actor's position evolves in time via stochastic differential equations. Using a state space representation for these stochastic processes and P\'olya-gamma data augmentation, we develop an efficient MCMC algorithm for posterior inference along with tractable procedures for online updating and forecasting of future networks. We evaluate performance in simulation studies, and consider an application to face-to-face contacts among individuals in a primary school.

Nonparametric Bayes dynamic modeling of relational data

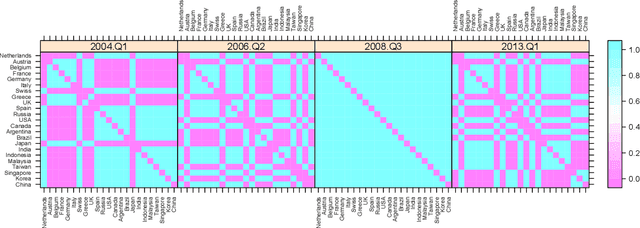
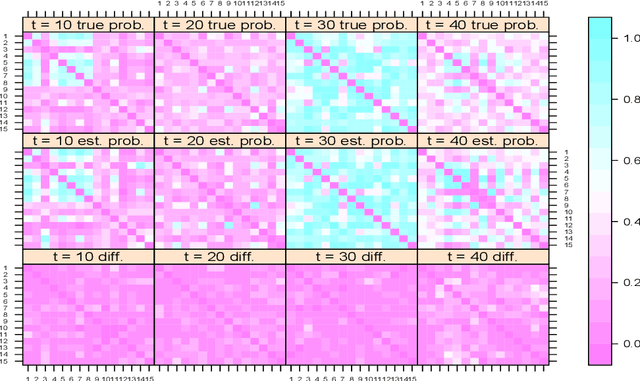
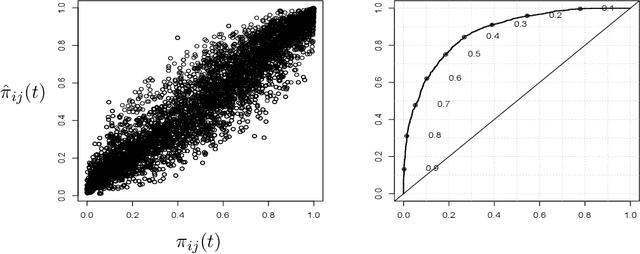
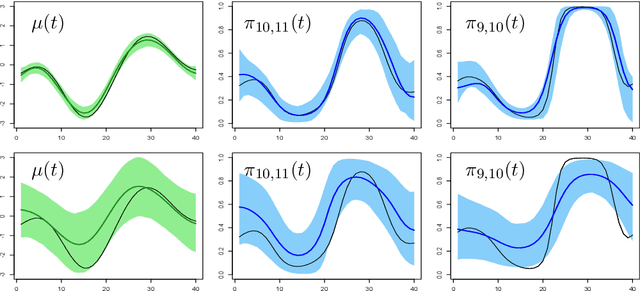
Symmetric binary matrices representing relations among entities are commonly collected in many areas. Our focus is on dynamically evolving binary relational matrices, with interest being in inference on the relationship structure and prediction. We propose a nonparametric Bayesian dynamic model, which reduces dimensionality in characterizing the binary matrix through a lower-dimensional latent space representation, with the latent coordinates evolving in continuous time via Gaussian processes. By using a logistic mapping function from the probability matrix space to the latent relational space, we obtain a flexible and computational tractable formulation. Employing P\`olya-Gamma data augmentation, an efficient Gibbs sampler is developed for posterior computation, with the dimension of the latent space automatically inferred. We provide some theoretical results on flexibility of the model, and illustrate performance via simulation experiments. We also consider an application to co-movements in world financial markets.

Locally adaptive factor processes for multivariate time series

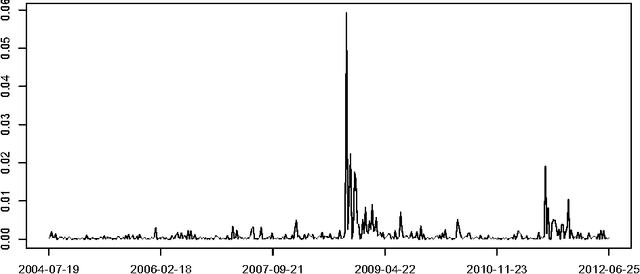
In modeling multivariate time series, it is important to allow time-varying smoothness in the mean and covariance process. In particular, there may be certain time intervals exhibiting rapid changes and others in which changes are slow. If such time-varying smoothness is not accounted for, one can obtain misleading inferences and predictions, with over-smoothing across erratic time intervals and under-smoothing across times exhibiting slow variation. This can lead to mis-calibration of predictive intervals, which can be substantially too narrow or wide depending on the time. We propose a locally adaptive factor process for characterizing multivariate mean-covariance changes in continuous time, allowing locally varying smoothness in both the mean and covariance matrix. This process is constructed utilizing latent dictionary functions evolving in time through nested Gaussian processes and linearly related to the observed data with a sparse mapping. Using a differential equation representation, we bypass usual computational bottlenecks in obtaining MCMC and online algorithms for approximate Bayesian inference. The performance is assessed in simulations and illustrated in a financial application.