Optimal lower bounds for logistic log-likelihoods

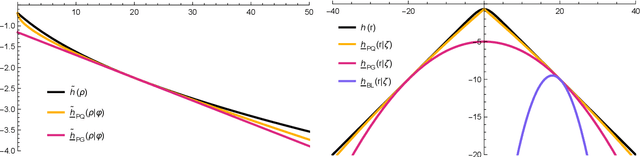
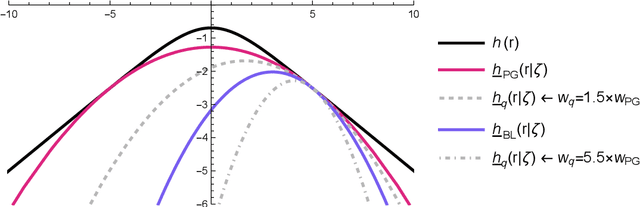
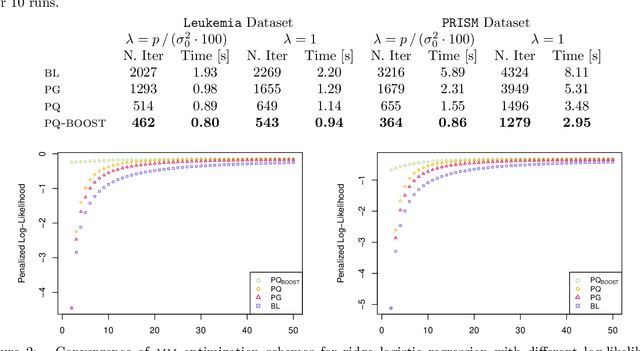
The logit transform is arguably the most widely-employed link function beyond linear settings. This transformation routinely appears in regression models for binary data and provides, either explicitly or implicitly, a core building-block within state-of-the-art methodologies for both classification and regression. Its widespread use, combined with the lack of analytical solutions for the optimization of general losses involving the logit transform, still motivates active research in computational statistics. Among the directions explored, a central one has focused on the design of tangent lower bounds for logistic log-likelihoods that can be tractably optimized, while providing a tight approximation of these log-likelihoods. Although progress along these lines has led to the development of effective minorize-maximize (MM) algorithms for point estimation and coordinate ascent variational inference schemes for approximate Bayesian inference under several logit models, the overarching focus in the literature has been on tangent quadratic minorizers. In fact, it is still unclear whether tangent lower bounds sharper than quadratic ones can be derived without undermining the tractability of the resulting minorizer. This article addresses such a challenging question through the design and study of a novel piece-wise quadratic lower bound that uniformly improves any tangent quadratic minorizer, including the sharpest ones, while admitting a direct interpretation in terms of the classical generalized lasso problem. As illustrated in a ridge logistic regression, this unique connection facilitates more effective implementations than those provided by available piece-wise bounds, while improving the convergence speed of quadratic ones.

Extended Stochastic Block Models

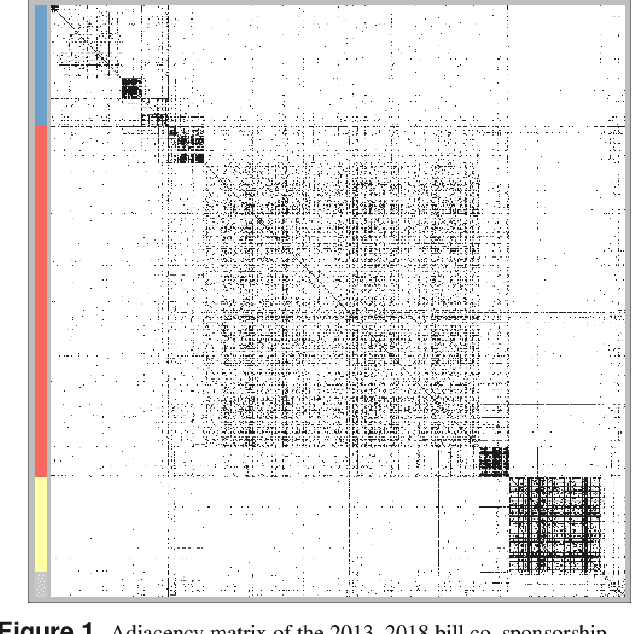
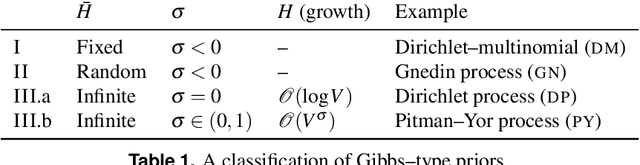
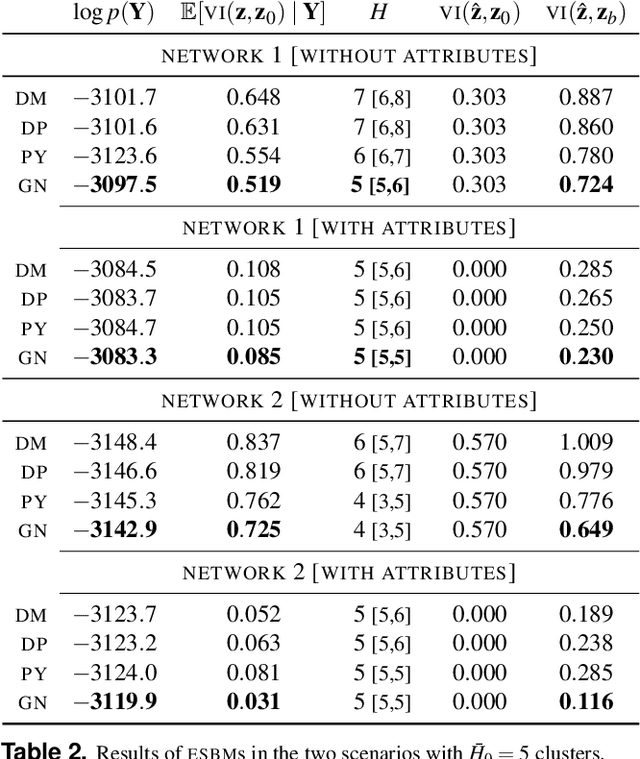
Stochastic block models (SBM) are widely used in network science due to their interpretable structure that allows inference on groups of nodes having common connectivity patterns. Although providing a well established model-based approach for community detection, such formulations are still the object of intense research to address the key problem of inferring the unknown number of communities. This has motivated the development of several probabilistic mechanisms to characterize the node partition process, covering solutions with fixed, random and infinite number of communities. In this article we provide a unified view of all these formulations within a single extended stochastic block model (ESBM), that relies on Gibbs-type processes and encompasses most existing representations as special cases. Connections with Bayesian nonparametric literature open up new avenues that allow the natural inclusion of several unexplored options to model the nodes partition process and to incorporate node attributes in a principled manner. Among these new alternatives, we focus on the Gnedin process as an example of a probabilistic mechanism with desirable theoretical properties and nice empirical performance. A collapsed Gibbs sampler that can be applied to the whole ESBM class is proposed, and refined methods for estimation, uncertainty quantification and model assessment are outlined. The performance of ESBM is assessed in simulations and an application to bill co-sponsorship networks in the Italian parliament, where we find key hidden block structures and core-periphery patterns.

A generalized Bayes framework for probabilistic clustering

Loss-based clustering methods, such as k-means and its variants, are standard tools for finding groups in data. However, the lack of quantification of uncertainty in the estimated clusters is a disadvantage. Model-based clustering based on mixture models provides an alternative, but such methods face computational problems and large sensitivity to the choice of kernel. This article proposes a generalized Bayes framework that bridges between these two paradigms through the use of Gibbs posteriors. In conducting Bayesian updating, the log likelihood is replaced by a loss function for clustering, leading to a rich family of clustering methods. The Gibbs posterior represents a coherent updating of Bayesian beliefs without needing to specify a likelihood for the data, and can be used for characterizing uncertainty in clustering. We consider losses based on Bregman divergence and pairwise similarities, and develop efficient deterministic algorithms for point estimation along with sampling algorithms for uncertainty quantification. Several existing clustering algorithms, including k-means, can be interpreted as generalized Bayes estimators under our framework, and hence we provide a method of uncertainty quantification for these approaches.