Sirio Legramanti
Extended Stochastic Block Models
Jul 16, 2020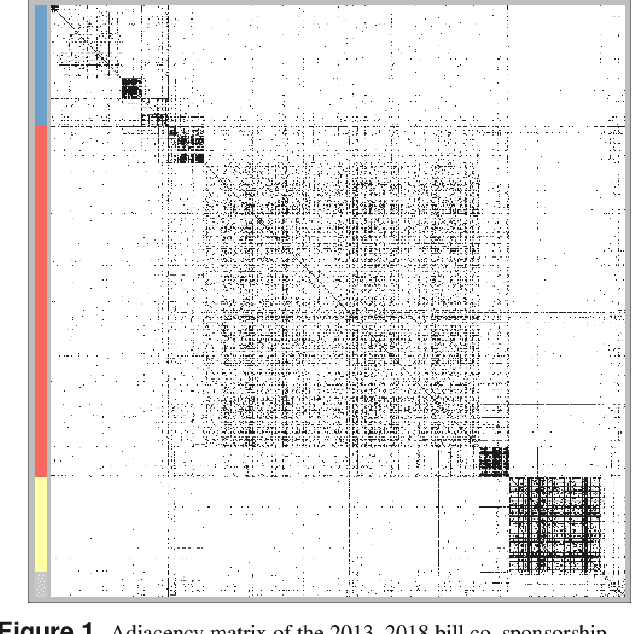
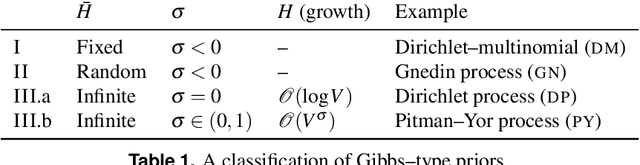
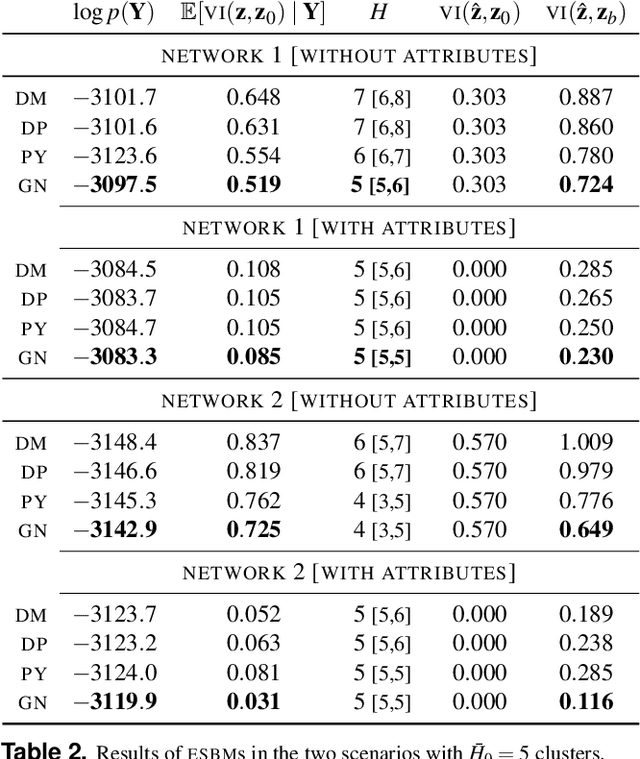

Abstract:Stochastic block models (SBM) are widely used in network science due to their interpretable structure that allows inference on groups of nodes having common connectivity patterns. Although providing a well established model-based approach for community detection, such formulations are still the object of intense research to address the key problem of inferring the unknown number of communities. This has motivated the development of several probabilistic mechanisms to characterize the node partition process, covering solutions with fixed, random and infinite number of communities. In this article we provide a unified view of all these formulations within a single extended stochastic block model (ESBM), that relies on Gibbs-type processes and encompasses most existing representations as special cases. Connections with Bayesian nonparametric literature open up new avenues that allow the natural inclusion of several unexplored options to model the nodes partition process and to incorporate node attributes in a principled manner. Among these new alternatives, we focus on the Gnedin process as an example of a probabilistic mechanism with desirable theoretical properties and nice empirical performance. A collapsed Gibbs sampler that can be applied to the whole ESBM class is proposed, and refined methods for estimation, uncertainty quantification and model assessment are outlined. The performance of ESBM is assessed in simulations and an application to bill co-sponsorship networks in the Italian parliament, where we find key hidden block structures and core-periphery patterns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge