Optimal lower bounds for logistic log-likelihoods
Paper and Code
Oct 14, 2024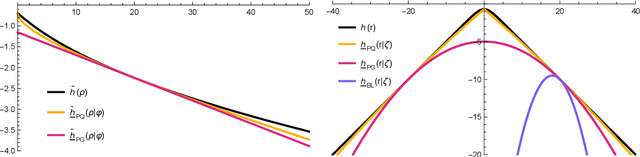
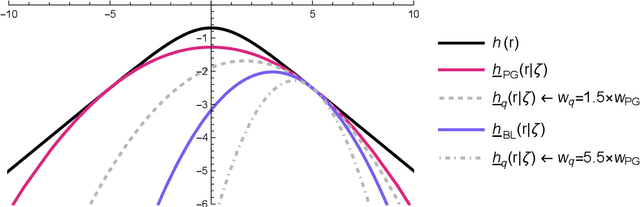
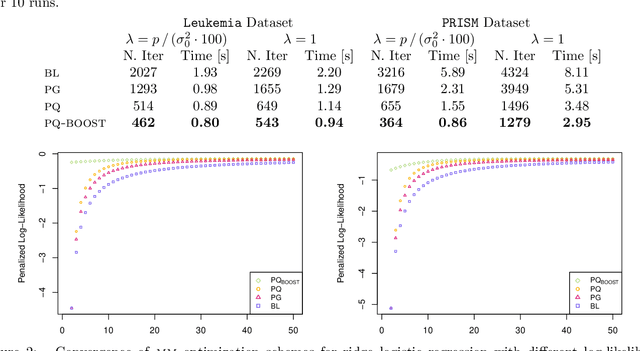
The logit transform is arguably the most widely-employed link function beyond linear settings. This transformation routinely appears in regression models for binary data and provides, either explicitly or implicitly, a core building-block within state-of-the-art methodologies for both classification and regression. Its widespread use, combined with the lack of analytical solutions for the optimization of general losses involving the logit transform, still motivates active research in computational statistics. Among the directions explored, a central one has focused on the design of tangent lower bounds for logistic log-likelihoods that can be tractably optimized, while providing a tight approximation of these log-likelihoods. Although progress along these lines has led to the development of effective minorize-maximize (MM) algorithms for point estimation and coordinate ascent variational inference schemes for approximate Bayesian inference under several logit models, the overarching focus in the literature has been on tangent quadratic minorizers. In fact, it is still unclear whether tangent lower bounds sharper than quadratic ones can be derived without undermining the tractability of the resulting minorizer. This article addresses such a challenging question through the design and study of a novel piece-wise quadratic lower bound that uniformly improves any tangent quadratic minorizer, including the sharpest ones, while admitting a direct interpretation in terms of the classical generalized lasso problem. As illustrated in a ridge logistic regression, this unique connection facilitates more effective implementations than those provided by available piece-wise bounds, while improving the convergence speed of quadratic ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge