Ilsang Ohn
Online Conformal Inference with Retrospective Adjustment for Faster Adaptation to Distribution Shift
Nov 06, 2025



Abstract:Conformal prediction has emerged as a powerful framework for constructing distribution-free prediction sets with guaranteed coverage assuming only the exchangeability assumption. However, this assumption is often violated in online environments where data distributions evolve over time. Several recent approaches have been proposed to address this limitation, but, typically, they slowly adapt to distribution shifts because they update predictions only in a forward manner, that is, they generate a prediction for a newly observed data point while previously computed predictions are not updated. In this paper, we propose a novel online conformal inference method with retrospective adjustment, which is designed to achieve faster adaptation to distributional shifts. Our method leverages regression approaches with efficient leave-one-out update formulas to retroactively adjust past predictions when new data arrive, thereby aligning the entire set of predictions with the most recent data distribution. Through extensive numerical studies performed on both synthetic and real-world data sets, we show that the proposed approach achieves faster coverage recalibration and improved statistical efficiency compared to existing online conformal prediction methods.
Knowledge Distillation of Uncertainty using Deep Latent Factor Model
Oct 22, 2025



Abstract:Deep ensembles deliver state-of-the-art, reliable uncertainty quantification, but their heavy computational and memory requirements hinder their practical deployments to real applications such as on-device AI. Knowledge distillation compresses an ensemble into small student models, but existing techniques struggle to preserve uncertainty partly because reducing the size of DNNs typically results in variation reduction. To resolve this limitation, we introduce a new method of distribution distillation (i.e. compressing a teacher ensemble into a student distribution instead of a student ensemble) called Gaussian distillation, which estimates the distribution of a teacher ensemble through a special Gaussian process called the deep latent factor model (DLF) by treating each member of the teacher ensemble as a realization of a certain stochastic process. The mean and covariance functions in the DLF model are estimated stably by using the expectation-maximization (EM) algorithm. By using multiple benchmark datasets, we demonstrate that the proposed Gaussian distillation outperforms existing baselines. In addition, we illustrate that Gaussian distillation works well for fine-tuning of language models and distribution shift problems.
Nonparametric estimation of a factorizable density using diffusion models
Jan 03, 2025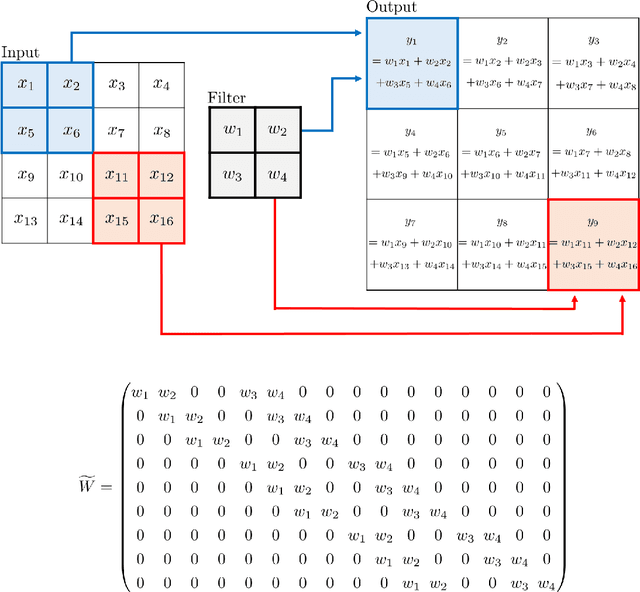
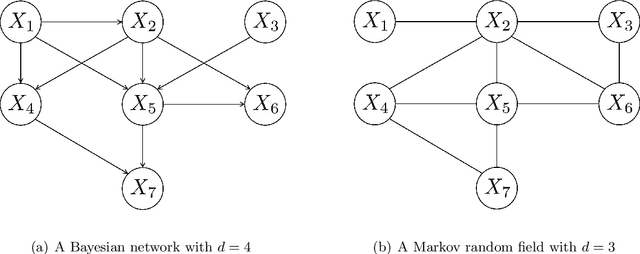
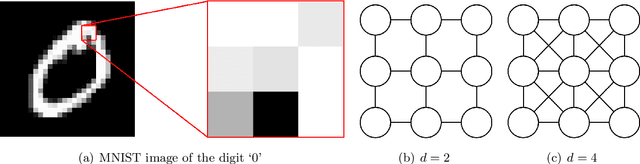
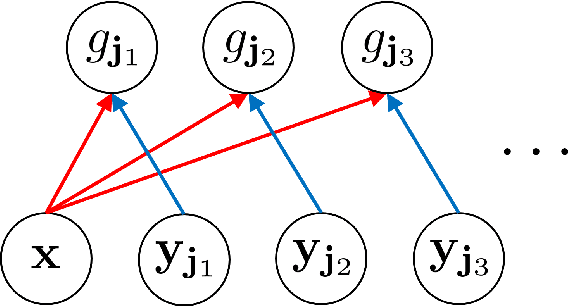
Abstract:In recent years, diffusion models, and more generally score-based deep generative models, have achieved remarkable success in various applications, including image and audio generation. In this paper, we view diffusion models as an implicit approach to nonparametric density estimation and study them within a statistical framework to analyze their surprising performance. A key challenge in high-dimensional statistical inference is leveraging low-dimensional structures inherent in the data to mitigate the curse of dimensionality. We assume that the underlying density exhibits a low-dimensional structure by factorizing into low-dimensional components, a property common in examples such as Bayesian networks and Markov random fields. Under suitable assumptions, we demonstrate that an implicit density estimator constructed from diffusion models adapts to the factorization structure and achieves the minimax optimal rate with respect to the total variation distance. In constructing the estimator, we design a sparse weight-sharing neural network architecture, where sparsity and weight-sharing are key features of practical architectures such as convolutional neural networks and recurrent neural networks.
A Bayesian sparse factor model with adaptive posterior concentration
May 29, 2023Abstract:In this paper, we propose a new Bayesian inference method for a high-dimensional sparse factor model that allows both the factor dimensionality and the sparse structure of the loading matrix to be inferred. The novelty is to introduce a certain dependence between the sparsity level and the factor dimensionality, which leads to adaptive posterior concentration while keeping computational tractability. We show that the posterior distribution asymptotically concentrates on the true factor dimensionality, and more importantly, this posterior consistency is adaptive to the sparsity level of the true loading matrix and the noise variance. We also prove that the proposed Bayesian model attains the optimal detection rate of the factor dimensionality in a more general situation than those found in the literature. Moreover, we obtain a near-optimal posterior concentration rate of the covariance matrix. Numerical studies are conducted and show the superiority of the proposed method compared with other competitors.
Masked Bayesian Neural Networks : Theoretical Guarantee and its Posterior Inference
May 24, 2023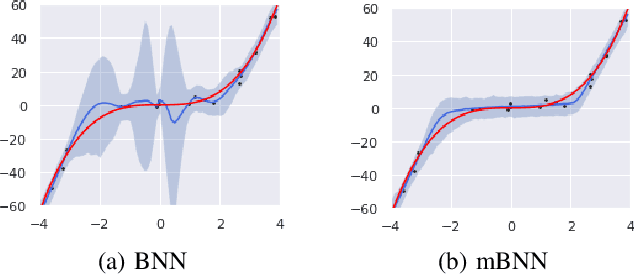
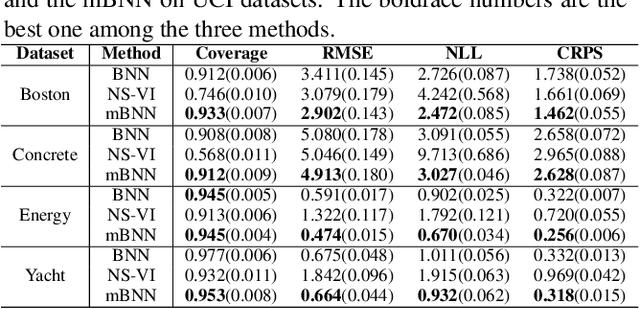
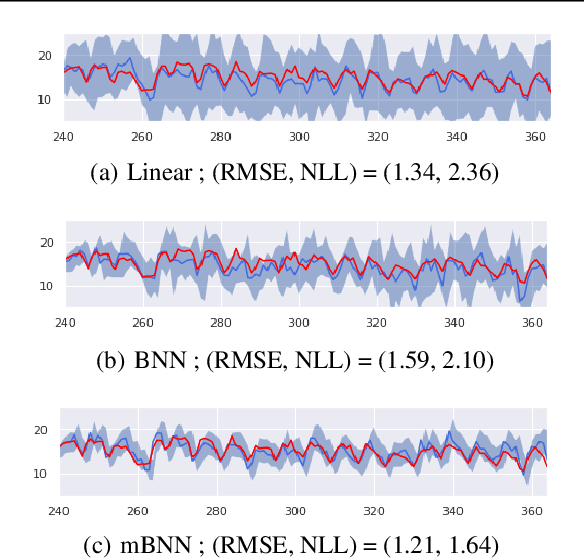
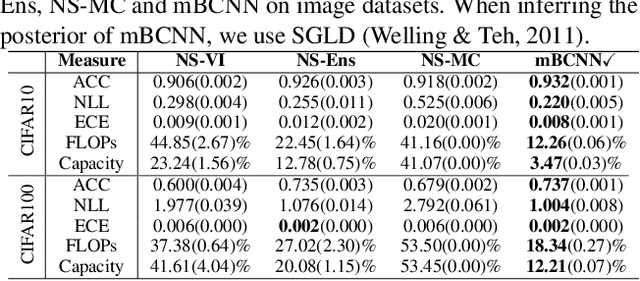
Abstract:Bayesian approaches for learning deep neural networks (BNN) have been received much attention and successfully applied to various applications. Particularly, BNNs have the merit of having better generalization ability as well as better uncertainty quantification. For the success of BNN, search an appropriate architecture of the neural networks is an important task, and various algorithms to find good sparse neural networks have been proposed. In this paper, we propose a new node-sparse BNN model which has good theoretical properties and is computationally feasible. We prove that the posterior concentration rate to the true model is near minimax optimal and adaptive to the smoothness of the true model. In particular the adaptiveness is the first of its kind for node-sparse BNNs. In addition, we develop a novel MCMC algorithm which makes the Bayesian inference of the node-sparse BNN model feasible in practice.
Intrinsic and extrinsic deep learning on manifolds
Feb 16, 2023Abstract:We propose extrinsic and intrinsic deep neural network architectures as general frameworks for deep learning on manifolds. Specifically, extrinsic deep neural networks (eDNNs) preserve geometric features on manifolds by utilizing an equivariant embedding from the manifold to its image in the Euclidean space. Moreover, intrinsic deep neural networks (iDNNs) incorporate the underlying intrinsic geometry of manifolds via exponential and log maps with respect to a Riemannian structure. Consequently, we prove that the empirical risk of the empirical risk minimizers (ERM) of eDNNs and iDNNs converge in optimal rates. Overall, The eDNNs framework is simple and easy to compute, while the iDNNs framework is accurate and fast converging. To demonstrate the utilities of our framework, various simulation studies, and real data analyses are presented with eDNNs and iDNNs.
The convergent Indian buffet process
Jun 16, 2022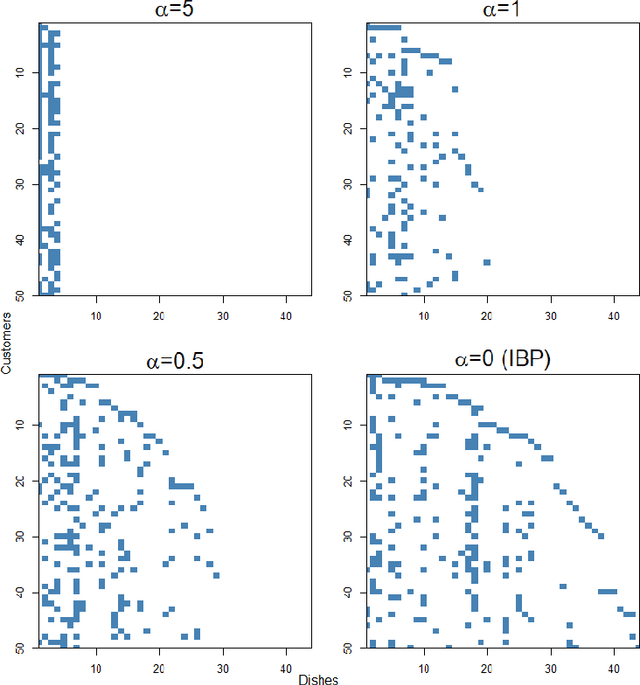
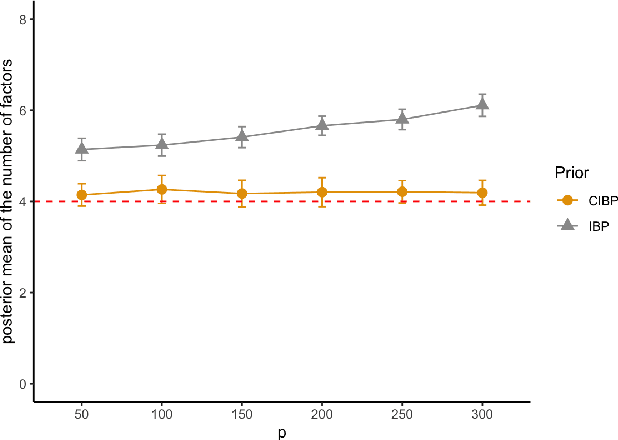
Abstract:We propose a new Bayesian nonparametric prior for latent feature models, which we call the convergent Indian buffet process (CIBP). We show that under the CIBP, the number of latent features is distributed as a Poisson distribution with the mean monotonically increasing but converging to a certain value as the number of objects goes to infinity. That is, the expected number of features is bounded above even when the number of objects goes to infinity, unlike the standard Indian buffet process under which the expected number of features increases with the number of objects. We provide two alternative representations of the CIBP based on a hierarchical distribution and a completely random measure, respectively, which are of independent interest. The proposed CIBP is assessed on a high-dimensional sparse factor model.
Masked Bayesian Neural Networks : Computation and Optimality
Jun 02, 2022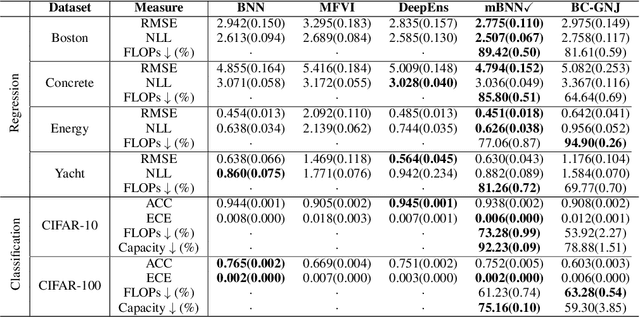
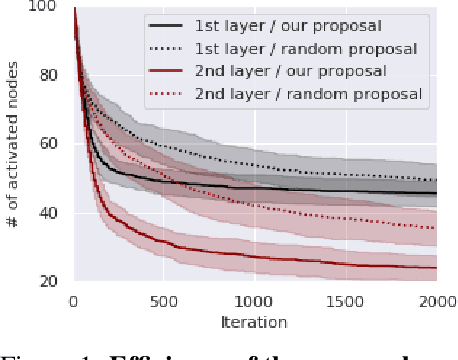
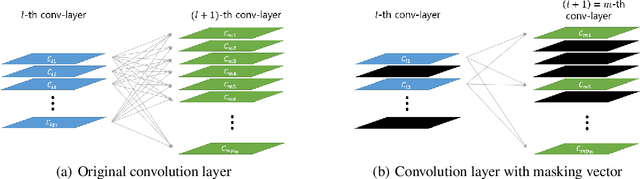
Abstract:As data size and computing power increase, the architectures of deep neural networks (DNNs) have been getting more complex and huge, and thus there is a growing need to simplify such complex and huge DNNs. In this paper, we propose a novel sparse Bayesian neural network (BNN) which searches a good DNN with an appropriate complexity. We employ the masking variables at each node which can turn off some nodes according to the posterior distribution to yield a nodewise sparse DNN. We devise a prior distribution such that the posterior distribution has theoretical optimalities (i.e. minimax optimality and adaptiveness), and develop an efficient MCMC algorithm. By analyzing several benchmark datasets, we illustrate that the proposed BNN performs well compared to other existing methods in the sense that it discovers well condensed DNN architectures with similar prediction accuracy and uncertainty quantification compared to large DNNs.
Learning fair representation with a parametric integral probability metric
Feb 17, 2022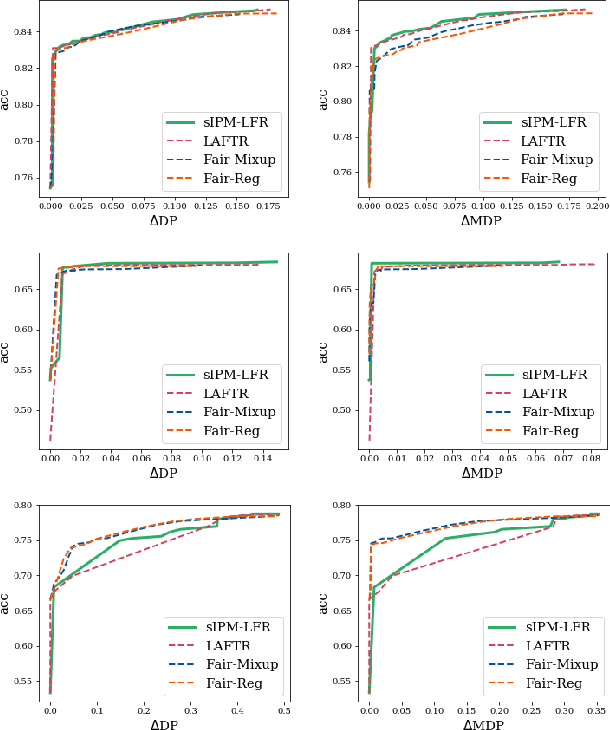
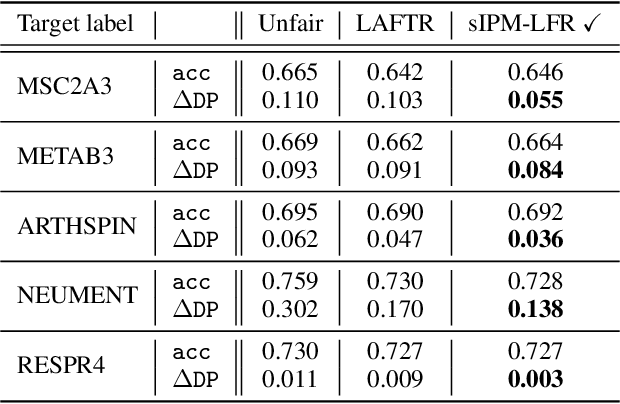
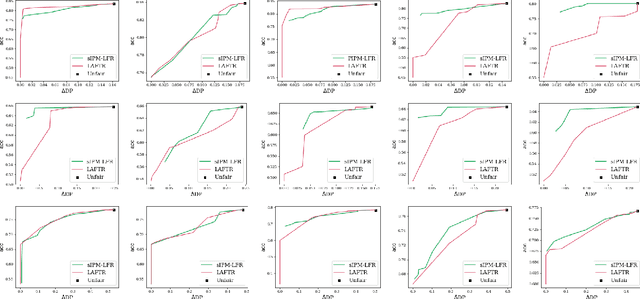
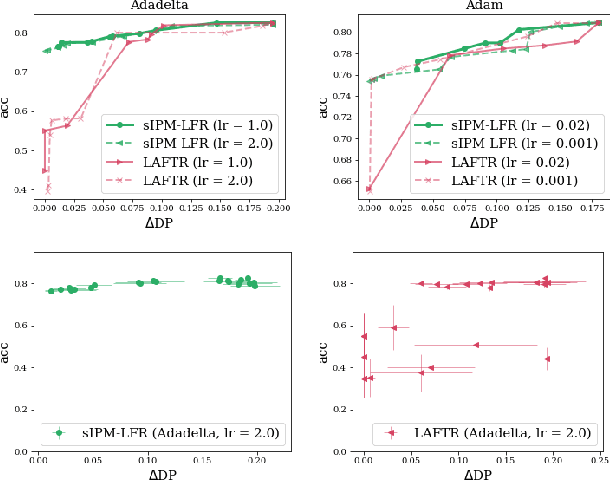
Abstract:As they have a vital effect on social decision-making, AI algorithms should be not only accurate but also fair. Among various algorithms for fairness AI, learning fair representation (LFR), whose goal is to find a fair representation with respect to sensitive variables such as gender and race, has received much attention. For LFR, the adversarial training scheme is popularly employed as is done in the generative adversarial network type algorithms. The choice of a discriminator, however, is done heuristically without justification. In this paper, we propose a new adversarial training scheme for LFR, where the integral probability metric (IPM) with a specific parametric family of discriminators is used. The most notable result of the proposed LFR algorithm is its theoretical guarantee about the fairness of the final prediction model, which has not been considered yet. That is, we derive theoretical relations between the fairness of representation and the fairness of the prediction model built on the top of the representation (i.e., using the representation as the input). Moreover, by numerical experiments, we show that our proposed LFR algorithm is computationally lighter and more stable, and the final prediction model is competitive or superior to other LFR algorithms using more complex discriminators.
SLIDE: a surrogate fairness constraint to ensure fairness consistency
Feb 07, 2022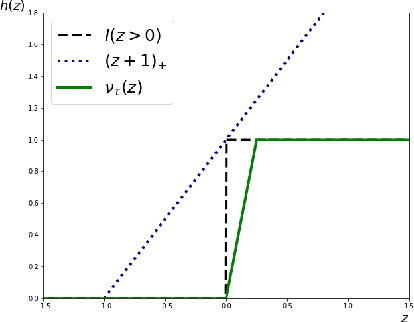
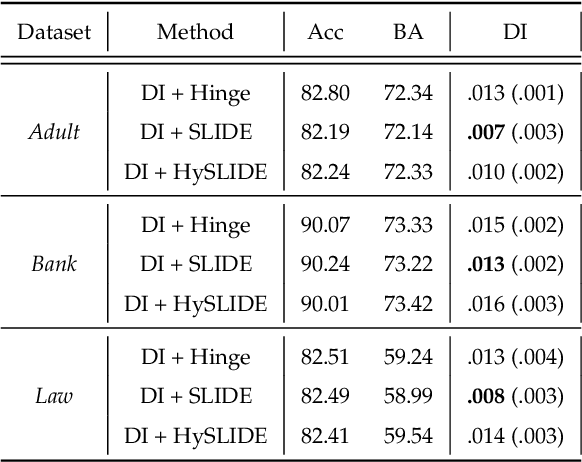
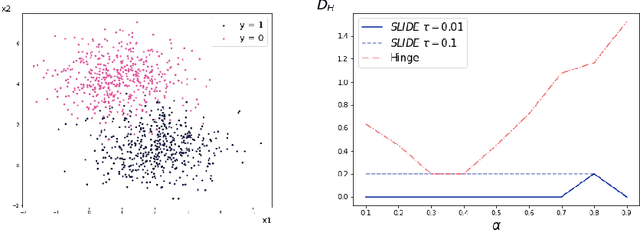
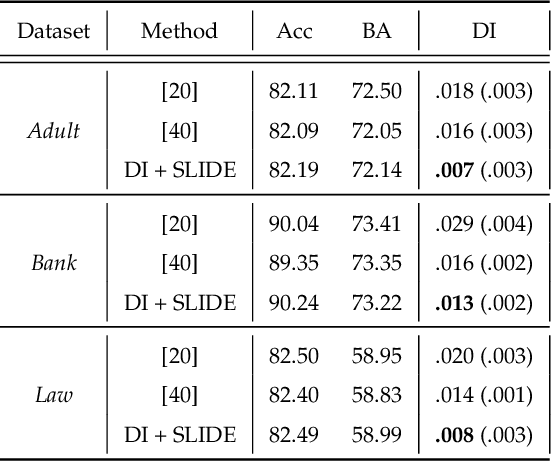
Abstract:As they have a vital effect on social decision makings, AI algorithms should be not only accurate and but also fair. Among various algorithms for fairness AI, learning a prediction model by minimizing the empirical risk (e.g., cross-entropy) subject to a given fairness constraint has received much attention. To avoid computational difficulty, however, a given fairness constraint is replaced by a surrogate fairness constraint as the 0-1 loss is replaced by a convex surrogate loss for classification problems. In this paper, we investigate the validity of existing surrogate fairness constraints and propose a new surrogate fairness constraint called SLIDE, which is computationally feasible and asymptotically valid in the sense that the learned model satisfies the fairness constraint asymptotically and achieves a fast convergence rate. Numerical experiments confirm that the SLIDE works well for various benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge