Nonconvex sparse regularization for deep neural networks and its optimality
Paper and Code
Mar 26, 2020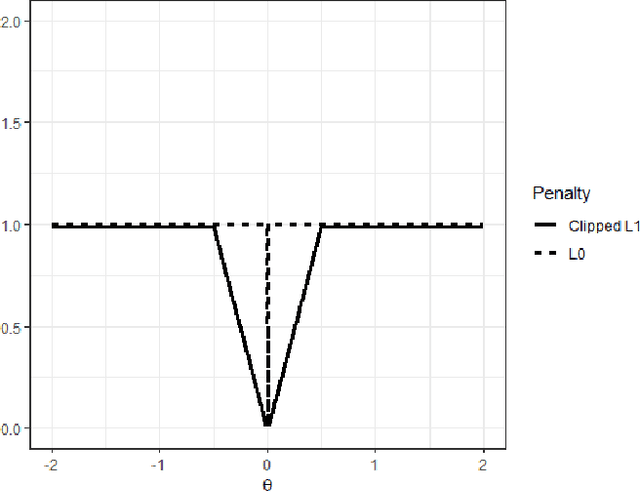

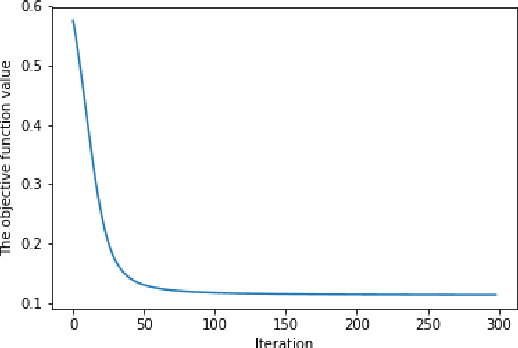
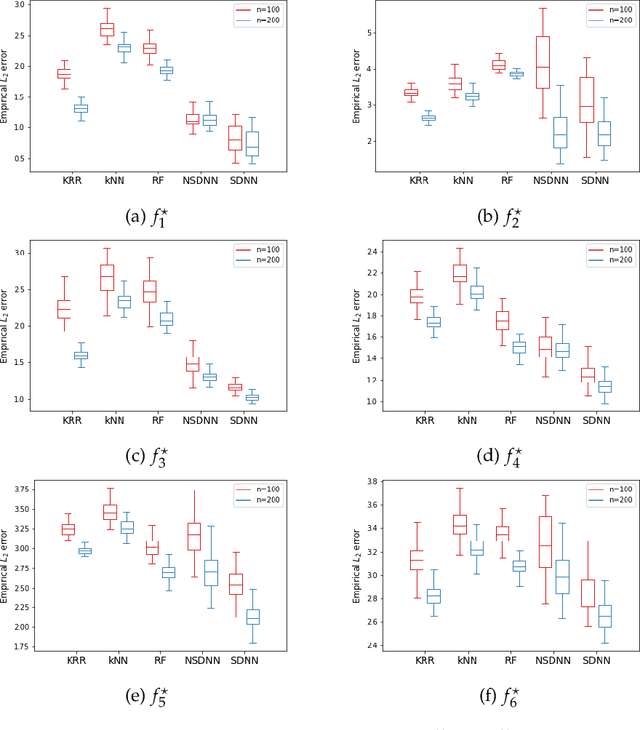
Recent theoretical studies proved that deep neural network (DNN) estimators obtained by minimizing empirical risk with a certain sparsity constraint can attain optimal convergence rates for regression and classification problems. However, the sparsity constraint requires to know certain properties of the true model, which are not available in practice. Moreover, computation is difficult due to the discrete nature of the sparsity constraint. In this paper, we propose a novel penalized estimation method for sparse DNNs, which resolves the aforementioned problems existing in the sparsity constraint. We establish an oracle inequality for the excess risk of the proposed sparse-penalized DNN estimator and derive convergence rates for several learning tasks. In particular, we prove that the sparse-penalized estimator can adaptively attain minimax convergence rates for various nonparametric regression problems. For computation, we develop an efficient gradient-based optimization algorithm that guarantees the monotonic reduction of the objective function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge