Adaptive variational Bayes: Optimality, computation and applications
Paper and Code
Sep 07, 2021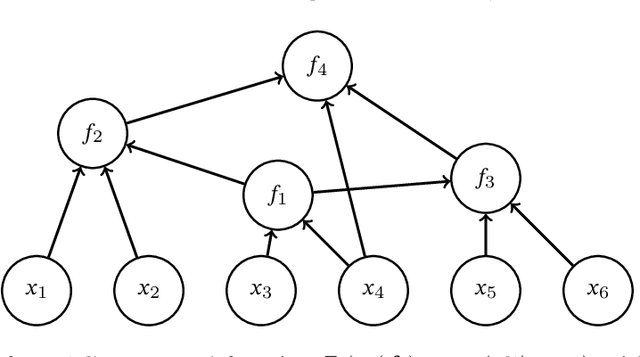
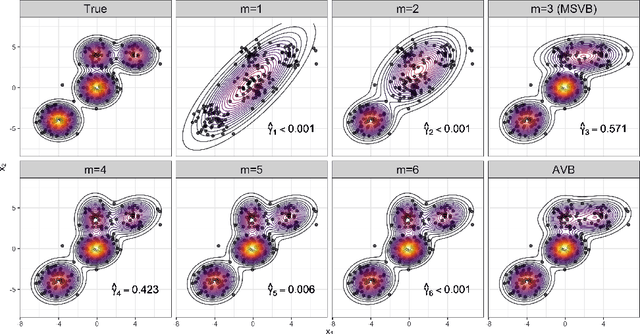
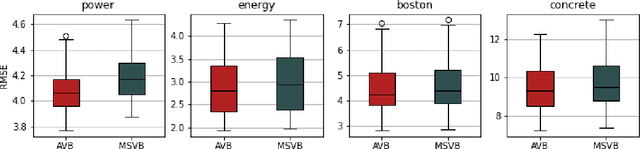
In this paper, we explore adaptive inference based on variational Bayes. Although a number of studies have been conducted to analyze contraction properties of variational posteriors, there is still a lack of a general and computationally tractable variational Bayes method that can achieve adaptive optimal contraction of the variational posterior. We propose a novel variational Bayes framework, called adaptive variational Bayes, which can operate on a collection of models with varying dimensions and structures. The proposed framework combines variational posteriors over individual models with certain weights to obtain a variational posterior over the entire model. It turns out that this combined variational posterior minimizes the Kullback-Leibler divergence to the original posterior distribution. We show that the proposed variational posterior achieves optimal contraction rates adaptively under very general conditions and attains model selection consistency when the true model structure exists. We apply the general results obtained for the adaptive variational Bayes to several examples including deep learning models and derive some new and adaptive inference results. Moreover, we consider the use of quasi-likelihood in our framework. We formulate conditions on the quasi-likelihood to ensure the adaptive optimality and discuss specific applications to stochastic block models and nonparametric regression with sub-Gaussian errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge