Nonparametric undirected graphical model selection using diffusion models

Undirected graphical models provide a fundamental framework for representing conditional independence structures among high-dimensional random variables. While undirected graphical model selection has become a central problem in high-dimensional statistics, most existing methods are restricted to parametric settings. In this paper, we develop a nonparametric approach to undirected graphical model selection based on diffusion models. Recent work has shown that diffusion models can adapt to the unknown graph structure of the underlying distribution, yet utilizing these models for explicit graph estimation remains unexplored. To bridge this gap, we introduce a novel diffusion-based method for nonparametric undirected graphical model selection. We establish the model selection consistency of the proposed method and demonstrate its empirical performance through extensive simulations and two real data analyses.

Stay Fair! Ensuring Group Fairness in Diffusion Models Across Guidance Scales

Diffusion models steer conditional generation with a tunable guidance scale to trade off prompt alignment and diversity. However, existing debiasing techniques are optimized for a single scale, degrading fairness when users adjust this parameter. We trace this behavior to a previously overlooked source by decomposing total bias into two components: a model bias and a guidance bias. While prior work primarily targets the former, we show that the guidance bias grows monotonically with the guidance scale, eventually dominating the high-guidance regimes users prefer. To address this, we extend Strong Demographic Parity to guidance and derive a condition under which the target distribution retains its group ratio across guidance scales. We propose StayFair, which leverages this condition to design fair guidance algorithms in both regimes. For classifier guidance, it equalizes the classifier's output distributions across groups; for classifier-free guidance, it shifts the null embedding by a prompt-dependent offset. Because StayFair modifies only the guidance step, it is orthogonal to model debiasing and can be layered onto existing fair diffusion models to extend their fairness across guidance scales. Across class-conditional and text-to-image generation, StayFair decouples fairness from the guidance scale without sacrificing image quality.

Multimodal Dataset Distillation Made Simple by Prototype-Guided Data Synthesis

Recent advances in multimodal learning have achieved remarkable success across diverse vision-language tasks. However, such progress heavily relies on large-scale image-text datasets, making training costly and inefficient. Prior efforts in dataset filtering and pruning attempt to mitigate this issue, but still require relatively large subsets to maintain performance and fail under very small subsets. Dataset distillation offers a promising alternative, yet existing multimodal dataset distillation methods require full-dataset training and joint optimization of image pixels and text features, making them architecture-dependent and limiting cross-architecture generalization. To overcome this, we propose a learning-free dataset distillation framework that eliminates the need for large-scale training and optimization while enhancing generalization across architectures. Our method uses CLIP to extract aligned image-text embeddings, obtains prototypes, and employs an unCLIP decoder to synthesize images, enabling efficient and scalable multimodal dataset distillation. Extensive experiments demonstrate that our approach consistently outperforms optimization-based dataset distillation and subset selection methods, achieving state-of-the-art cross-architecture generalization.

Distributionally Robust Classification for Multi-source Unsupervised Domain Adaptation

Unsupervised domain adaptation (UDA) is a statistical learning problem when the distribution of training (source) data is different from that of test (target) data. In this setting, one has access to labeled data only from the source domain and unlabeled data from the target domain. The central objective is to leverage the source data and the unlabeled target data to build models that generalize to the target domain. Despite its potential, existing UDA approaches often struggle in practice, particularly in scenarios where the target domain offers only limited unlabeled data or spurious correlations dominate the source domain. To address these challenges, we propose a novel distributionally robust learning framework that models uncertainty in both the covariate distribution and the conditional label distribution. Our approach is motivated by the multi-source domain adaptation setting but is also directly applicable to the single-source scenario, making it versatile in practice. We develop an efficient learning algorithm that can be seamlessly integrated with existing UDA methods. Extensive experiments under various distribution shift scenarios show that our method consistently outperforms strong baselines, especially when target data are extremely scarce.

Fairness Through Matching

Group fairness requires that different protected groups, characterized by a given sensitive attribute, receive equal outcomes overall. Typically, the level of group fairness is measured by the statistical gap between predictions from different protected groups. In this study, we reveal an implicit property of existing group fairness measures, which provides an insight into how the group-fair models behave. Then, we develop a new group-fair constraint based on this implicit property to learn group-fair models. To do so, we first introduce a notable theoretical observation: every group-fair model has an implicitly corresponding transport map between the input spaces of each protected group. Based on this observation, we introduce a new group fairness measure termed Matched Demographic Parity (MDP), which quantifies the averaged gap between predictions of two individuals (from different protected groups) matched by a given transport map. Then, we prove that any transport map can be used in MDP to learn group-fair models, and develop a novel algorithm called Fairness Through Matching (FTM), which learns a group-fair model using MDP constraint with an user-specified transport map. We specifically propose two favorable types of transport maps for MDP, based on the optimal transport theory, and discuss their advantages. Experiments reveal that FTM successfully trains group-fair models with certain desirable properties by choosing the transport map accordingly.

Nonparametric estimation of a factorizable density using diffusion models

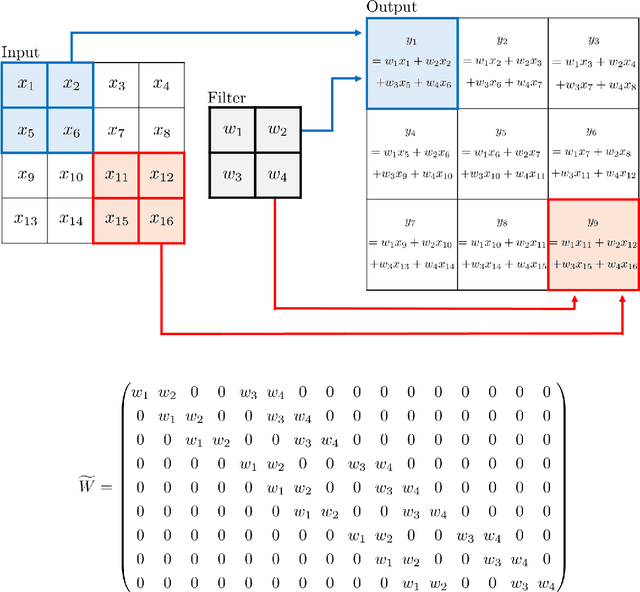
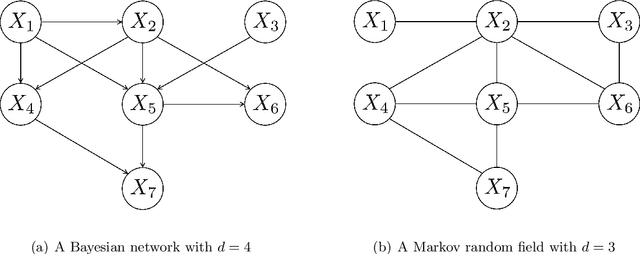
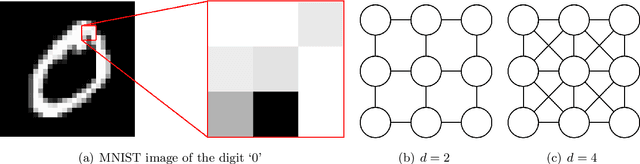
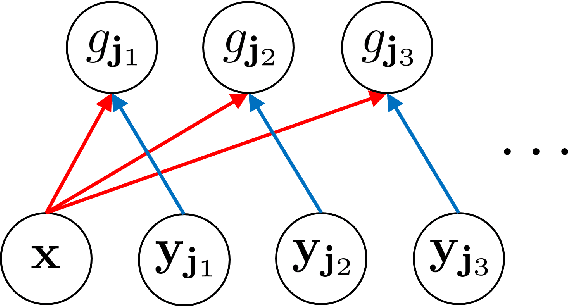
In recent years, diffusion models, and more generally score-based deep generative models, have achieved remarkable success in various applications, including image and audio generation. In this paper, we view diffusion models as an implicit approach to nonparametric density estimation and study them within a statistical framework to analyze their surprising performance. A key challenge in high-dimensional statistical inference is leveraging low-dimensional structures inherent in the data to mitigate the curse of dimensionality. We assume that the underlying density exhibits a low-dimensional structure by factorizing into low-dimensional components, a property common in examples such as Bayesian networks and Markov random fields. Under suitable assumptions, we demonstrate that an implicit density estimator constructed from diffusion models adapts to the factorization structure and achieves the minimax optimal rate with respect to the total variation distance. In constructing the estimator, we design a sparse weight-sharing neural network architecture, where sparsity and weight-sharing are key features of practical architectures such as convolutional neural networks and recurrent neural networks.

A likelihood approach to nonparametric estimation of a singular distribution using deep generative models

We investigate statistical properties of a likelihood approach to nonparametric estimation of a singular distribution using deep generative models. More specifically, a deep generative model is used to model high-dimensional data that are assumed to concentrate around some low-dimensional structure. Estimating the distribution supported on this low-dimensional structure such as a low-dimensional manifold is challenging due to its singularity with respect to the Lebesgue measure in the ambient space. In the considered model, a usual likelihood approach can fail to estimate the target distribution consistently due to the singularity. We prove that a novel and effective solution exists by perturbing the data with an instance noise which leads to consistent estimation of the underlying distribution with desirable convergence rates. We also characterize the class of distributions that can be efficiently estimated via deep generative models. This class is sufficiently general to contain various structured distributions such as product distributions, classically smooth distributions and distributions supported on a low-dimensional manifold. Our analysis provides some insights on how deep generative models can avoid the curse of dimensionality for nonparametric distribution estimation. We conduct thorough simulation study and real data analysis to empirically demonstrate that the proposed data perturbation technique improves the estimation performance significantly.