The convergent Indian buffet process
Paper and Code
Jun 16, 2022
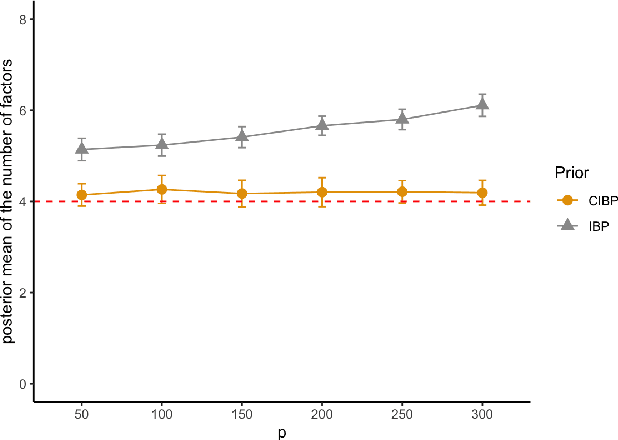
We propose a new Bayesian nonparametric prior for latent feature models, which we call the convergent Indian buffet process (CIBP). We show that under the CIBP, the number of latent features is distributed as a Poisson distribution with the mean monotonically increasing but converging to a certain value as the number of objects goes to infinity. That is, the expected number of features is bounded above even when the number of objects goes to infinity, unlike the standard Indian buffet process under which the expected number of features increases with the number of objects. We provide two alternative representations of the CIBP based on a hierarchical distribution and a completely random measure, respectively, which are of independent interest. The proposed CIBP is assessed on a high-dimensional sparse factor model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge