Mu Niu
Intrinsic Bayesian Optimisation on Complex Constrained Domain
Jan 29, 2023



Abstract:Motivated by the success of Bayesian optimisation algorithms in the Euclidean space, we propose a novel approach to construct Intrinsic Bayesian optimisation (In-BO) on manifolds with a primary focus on complex constrained domains or irregular-shaped spaces arising as submanifolds of R2, R3 and beyond. Data may be collected in a spatial domain but restricted to a complex or intricately structured region corresponding to a geographic feature, such as lakes. Traditional Bayesian Optimisation (Tra-BO) defined with a Radial basis function (RBF) kernel cannot accommodate these complex constrained conditions. The In-BO uses the Sparse Intrinsic Gaussian Processes (SIn-GP) surrogate model to take into account the geometric structure of the manifold. SInGPs are constructed using the heat kernel of the manifold which is estimated as the transition density of the Brownian Motion on manifolds. The efficiency of In-BO is demonstrated through simulation studies on a U-shaped domain, a Bitten torus, and a real dataset from the Aral sea. Its performance is compared to that of traditional BO, which is defined in Euclidean space.
Intrinsic Gaussian Process on Unknown Manifolds with Probabilistic Metrics
Jan 16, 2023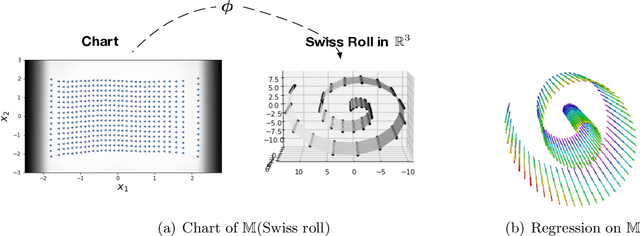

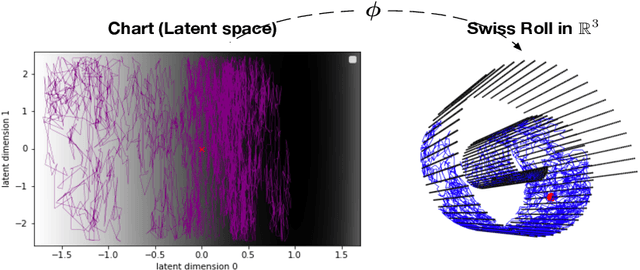
Abstract:This article presents a novel approach to construct Intrinsic Gaussian Processes for regression on unknown manifolds with probabilistic metrics (GPUM) in point clouds. In many real world applications, one often encounters high dimensional data (e.g. point cloud data) centred around some lower dimensional unknown manifolds. The geometry of manifold is in general different from the usual Euclidean geometry. Naively applying traditional smoothing methods such as Euclidean Gaussian Processes (GPs) to manifold valued data and so ignoring the geometry of the space can potentially lead to highly misleading predictions and inferences. A manifold embedded in a high dimensional Euclidean space can be well described by a probabilistic mapping function and the corresponding latent space. We investigate the geometrical structure of the unknown manifolds using the Bayesian Gaussian Processes latent variable models(BGPLVM) and Riemannian geometry. The distribution of the metric tensor is learned using BGPLVM. The boundary of the resulting manifold is defined based on the uncertainty quantification of the mapping. We use the the probabilistic metric tensor to simulate Brownian Motion paths on the unknown manifold. The heat kernel is estimated as the transition density of Brownian Motion and used as the covariance functions of GPUM. The applications of GPUM are illustrated in the simulation studies on the Swiss roll, high dimensional real datasets of WiFi signals and image data examples. Its performance is compared with the Graph Laplacian GP, Graph Matern GP and Euclidean GP.
Extrinsic Bayesian Optimizations on Manifolds
Dec 29, 2022Abstract:We propose an extrinsic Bayesian optimization (eBO) framework for general optimization problems on manifolds. Bayesian optimization algorithms build a surrogate of the objective function by employing Gaussian processes and quantify the uncertainty in that surrogate by deriving an acquisition function. This acquisition function represents the probability of improvement based on the kernel of the Gaussian process, which guides the search in the optimization process. The critical challenge for designing Bayesian optimization algorithms on manifolds lies in the difficulty of constructing valid covariance kernels for Gaussian processes on general manifolds. Our approach is to employ extrinsic Gaussian processes by first embedding the manifold onto some higher dimensional Euclidean space via equivariant embeddings and then constructing a valid covariance kernel on the image manifold after the embedding. This leads to efficient and scalable algorithms for optimization over complex manifolds. Simulation study and real data analysis are carried out to demonstrate the utilities of our eBO framework by applying the eBO to various optimization problems over manifolds such as the sphere, the Grassmannian, and the manifold of positive definite matrices.
Heat kernel and intrinsic Gaussian processes on manifolds
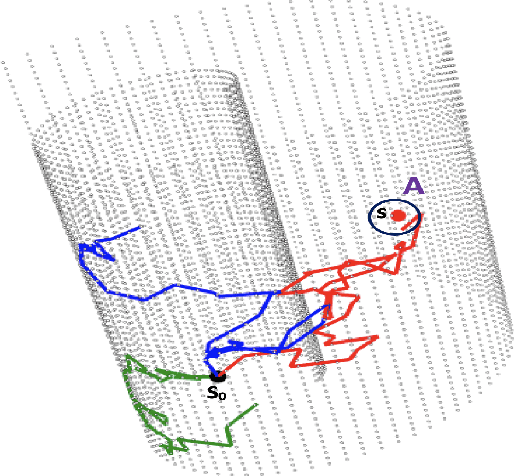
Jun 25, 2020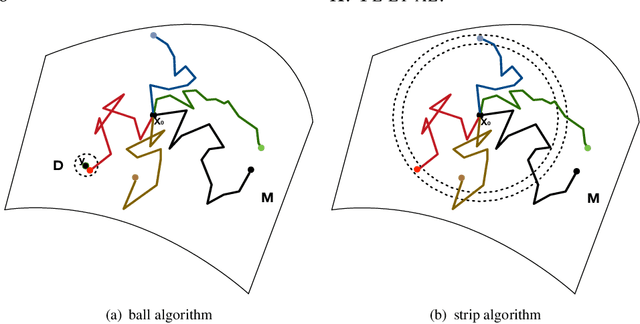

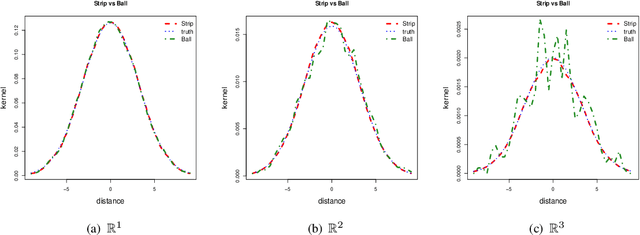

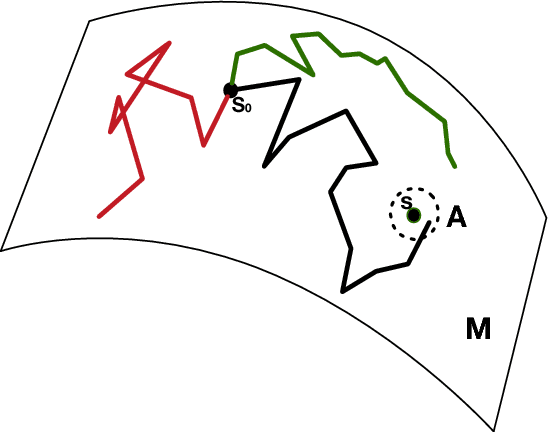
Abstract:There is an increasing interest in the problem of nonparametric regression like Gaussian processes with predictors locating on manifold. Some recent researches developed intrinsic Gaussian processes by using the transition density of the Brownian motion on submanifolds of $\mathbb R^2$ and $\mathbb R^3$ to approximate the heat kernels. {However}, when the dimension of a manifold is bigger than two, the existing method struggled to get good estimation of the heat kernel. In this work, we propose an intrinsic approach of constructing the Gaussian process on \if more \fi general manifolds \if {\color{red} in the matrix Lie groups} \fi such as orthogonal groups, unitary groups, Stiefel manifolds and Grassmannian manifolds. The heat kernel is estimated by simulating Brownian motion sample paths via the exponential map, which does not depend on the embedding of the manifold. To be more precise, this intrinsic method has the following features: (i) it is effective for high dimensional manifolds; (ii) it is applicable to arbitrary manifolds; (iii) it does not require the global parametrisation or embedding which may introduce redundant parameters; (iv) results obtained by this method do not depend on the ambient space of the manifold. Based on this method, we propose the ball algorithm for arbitrary manifolds and the strip algorithm for manifolds with extra symmetries, which is both theoretically proven and numerically tested to be much more efficient than the ball algorithm. A regression example on the projective space of dimension eight is given in this work, which demonstrates that our intrinsic method for Gaussian process is practically effective in great generality.
Intrinsic Gaussian processes on complex constrained domains
Jan 03, 2018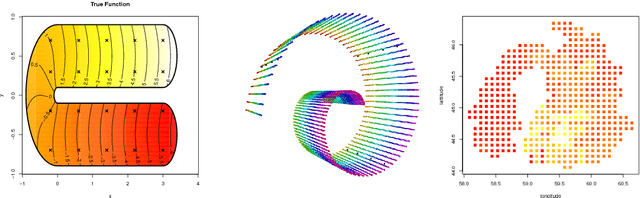


Abstract:We propose a class of intrinsic Gaussian processes (in-GPs) for interpolation, regression and classification on manifolds with a primary focus on complex constrained domains or irregular shaped spaces arising as subsets or submanifolds of R, R2, R3 and beyond. For example, in-GPs can accommodate spatial domains arising as complex subsets of Euclidean space. in-GPs respect the potentially complex boundary or interior conditions as well as the intrinsic geometry of the spaces. The key novelty of the proposed approach is to utilise the relationship between heat kernels and the transition density of Brownian motion on manifolds for constructing and approximating valid and computationally feasible covariance kernels. This enables in-GPs to be practically applied in great generality, while existing approaches for smoothing on constrained domains are limited to simple special cases. The broad utilities of the in-GP approach is illustrated through simulation studies and data examples.
Spatio-temporal Gaussian processes modeling of dynamical systems in systems biology
Oct 17, 2016
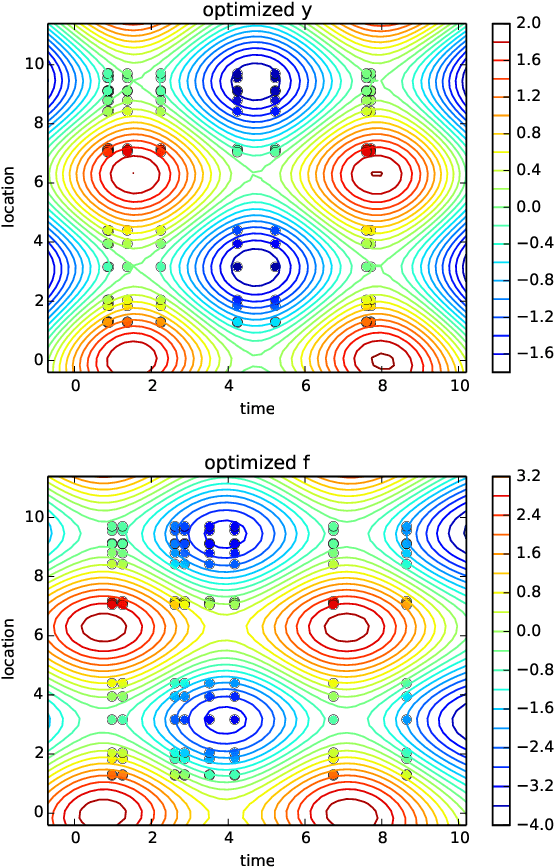
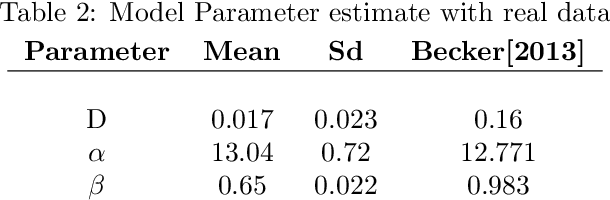
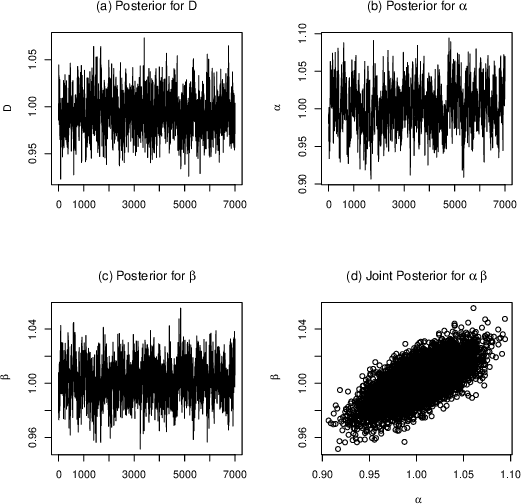
Abstract:Quantitative modeling of post-transcriptional regulation process is a challenging problem in systems biology. A mechanical model of the regulatory process needs to be able to describe the available spatio-temporal protein concentration and mRNA expression data and recover the continuous spatio-temporal fields. Rigorous methods are required to identify model parameters. A promising approach to deal with these difficulties is proposed using Gaussian process as a prior distribution over the latent function of protein concentration and mRNA expression. In this study, we consider a partial differential equation mechanical model with differential operators and latent function. Since the operators at stake are linear, the information from the physical model can be encoded into the kernel function. Hybrid Monte Carlo methods are employed to carry out Bayesian inference of the partial differential equation parameters and Gaussian process kernel parameters. The spatio-temporal field of protein concentration and mRNA expression are reconstructed without explicitly solving the partial differential equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge