Diffusion Model for Slate Recommendation

Slate recommendation is a technique commonly used on streaming platforms and e-commerce sites to present multiple items together. A significant challenge with slate recommendation is managing the complex combinatorial choice space. Traditional methods often simplify this problem by assuming users engage with only one item at a time. However, this simplification does not reflect the reality, as users often interact with multiple items simultaneously. In this paper, we address the general slate recommendation problem, which accounts for simultaneous engagement with multiple items. We propose a generative approach using Diffusion Models, leveraging their ability to learn structures in high-dimensional data. Our model generates high-quality slates that maximize user satisfaction by overcoming the challenges of the combinatorial choice space. Furthermore, our approach enhances the diversity of recommendations. Extensive offline evaluations on applications such as music playlist generation and e-commerce bundle recommendations show that our model outperforms state-of-the-art baselines in both relevance and diversity.

In-context Exploration-Exploitation for Reinforcement Learning

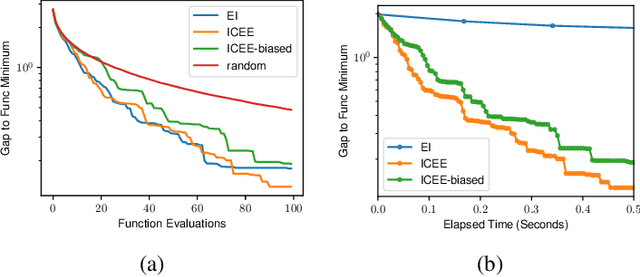
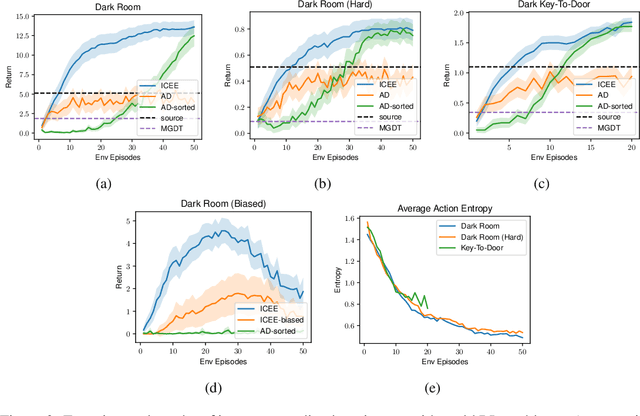
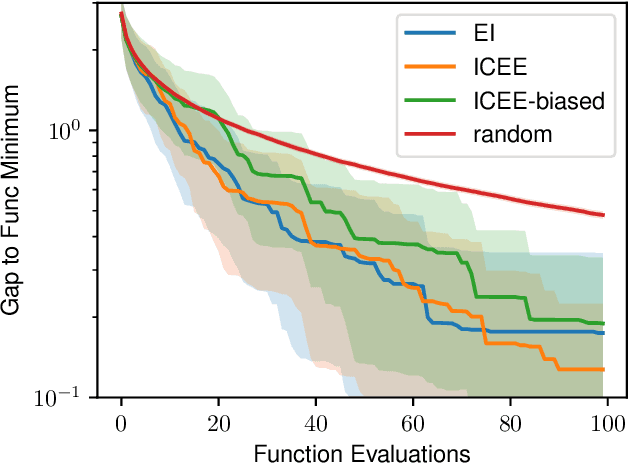
In-context learning is a promising approach for online policy learning of offline reinforcement learning (RL) methods, which can be achieved at inference time without gradient optimization. However, this method is hindered by significant computational costs resulting from the gathering of large training trajectory sets and the need to train large Transformer models. We address this challenge by introducing an In-context Exploration-Exploitation (ICEE) algorithm, designed to optimize the efficiency of in-context policy learning. Unlike existing models, ICEE performs an exploration-exploitation trade-off at inference time within a Transformer model, without the need for explicit Bayesian inference. Consequently, ICEE can solve Bayesian optimization problems as efficiently as Gaussian process biased methods do, but in significantly less time. Through experiments in grid world environments, we demonstrate that ICEE can learn to solve new RL tasks using only tens of episodes, marking a substantial improvement over the hundreds of episodes needed by the previous in-context learning method.

Automatic Music Playlist Generation via Simulation-based Reinforcement Learning

Personalization of playlists is a common feature in music streaming services, but conventional techniques, such as collaborative filtering, rely on explicit assumptions regarding content quality to learn how to make recommendations. Such assumptions often result in misalignment between offline model objectives and online user satisfaction metrics. In this paper, we present a reinforcement learning framework that solves for such limitations by directly optimizing for user satisfaction metrics via the use of a simulated playlist-generation environment. Using this simulator we develop and train a modified Deep Q-Network, the action head DQN (AH-DQN), in a manner that addresses the challenges imposed by the large state and action space of our RL formulation. The resulting policy is capable of making recommendations from large and dynamic sets of candidate items with the expectation of maximizing consumption metrics. We analyze and evaluate agents offline via simulations that use environment models trained on both public and proprietary streaming datasets. We show how these agents lead to better user-satisfaction metrics compared to baseline methods during online A/B tests. Finally, we demonstrate that performance assessments produced from our simulator are strongly correlated with observed online metric results.

A Strong Baseline for Batch Imitation Learning

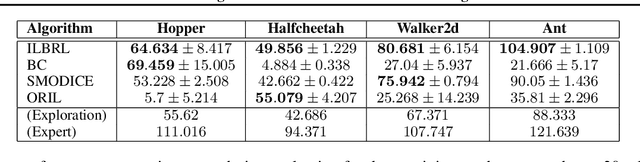
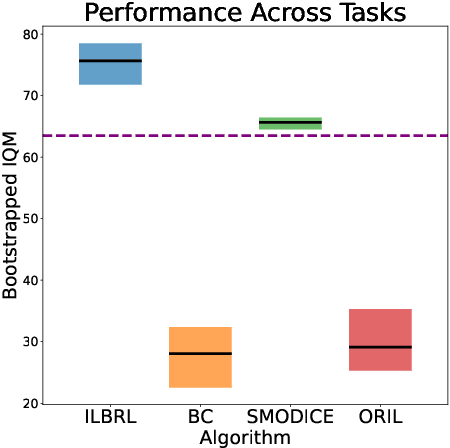
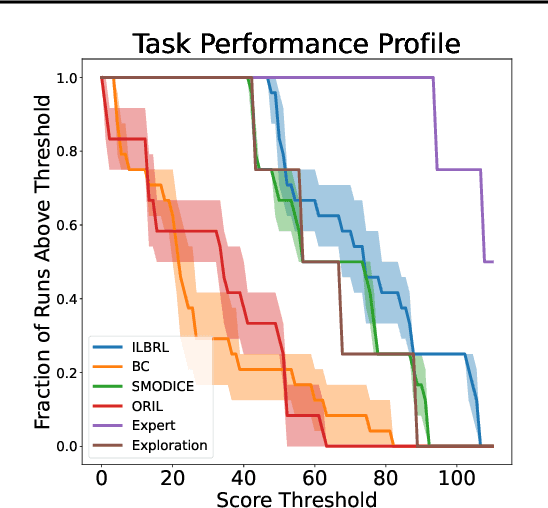
Imitation of expert behaviour is a highly desirable and safe approach to the problem of sequential decision making. We provide an easy-to-implement, novel algorithm for imitation learning under a strict data paradigm, in which the agent must learn solely from data collected a priori. This paradigm allows our algorithm to be used for environments in which safety or cost are of critical concern. Our algorithm requires no additional hyper-parameter tuning beyond any standard batch reinforcement learning (RL) algorithm, making it an ideal baseline for such data-strict regimes. Furthermore, we provide formal sample complexity guarantees for the algorithm in finite Markov Decision Problems. In doing so, we formally demonstrate an unproven claim from Kearns & Singh (1998). On the empirical side, our contribution is twofold. First, we develop a practical, robust and principled evaluation protocol for offline RL methods, making use of only the dataset provided for model selection. This stands in contrast to the vast majority of previous works in offline RL, which tune hyperparameters on the evaluation environment, limiting the practical applicability when deployed in new, cost-critical environments. As such, we establish precedent for the development and fair evaluation of offline RL algorithms. Second, we evaluate our own algorithm on challenging continuous control benchmarks, demonstrating its practical applicability and competitiveness with state-of-the-art performance, despite being a simpler algorithm.

Intrinsic Gaussian Process on Unknown Manifolds with Probabilistic Metrics

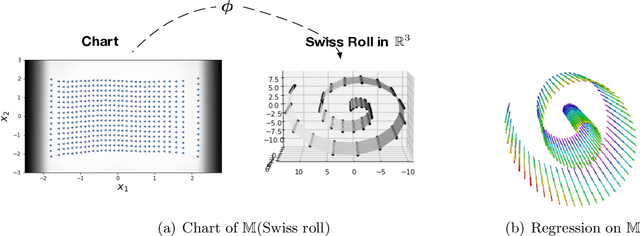
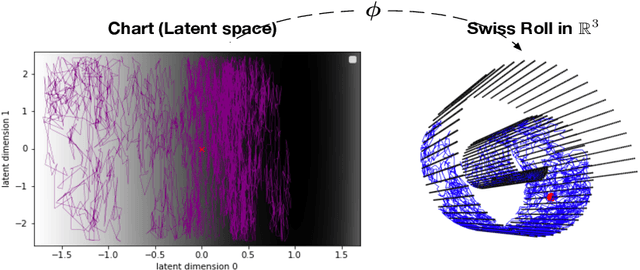
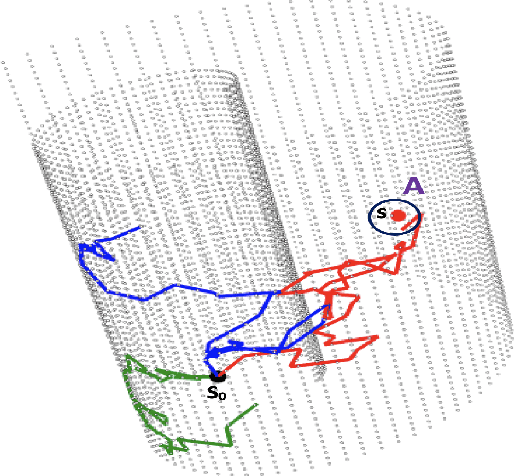
This article presents a novel approach to construct Intrinsic Gaussian Processes for regression on unknown manifolds with probabilistic metrics (GPUM) in point clouds. In many real world applications, one often encounters high dimensional data (e.g. point cloud data) centred around some lower dimensional unknown manifolds. The geometry of manifold is in general different from the usual Euclidean geometry. Naively applying traditional smoothing methods such as Euclidean Gaussian Processes (GPs) to manifold valued data and so ignoring the geometry of the space can potentially lead to highly misleading predictions and inferences. A manifold embedded in a high dimensional Euclidean space can be well described by a probabilistic mapping function and the corresponding latent space. We investigate the geometrical structure of the unknown manifolds using the Bayesian Gaussian Processes latent variable models(BGPLVM) and Riemannian geometry. The distribution of the metric tensor is learned using BGPLVM. The boundary of the resulting manifold is defined based on the uncertainty quantification of the mapping. We use the the probabilistic metric tensor to simulate Brownian Motion paths on the unknown manifold. The heat kernel is estimated as the transition density of Brownian Motion and used as the covariance functions of GPUM. The applications of GPUM are illustrated in the simulation studies on the Swiss roll, high dimensional real datasets of WiFi signals and image data examples. Its performance is compared with the Graph Laplacian GP, Graph Matern GP and Euclidean GP.

Model Selection for Production System via Automated Online Experiments

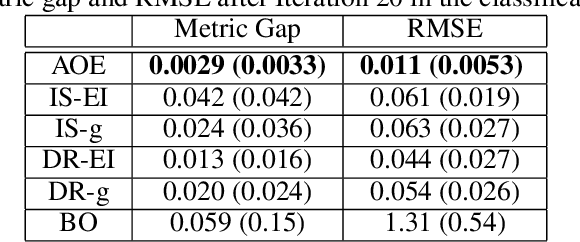
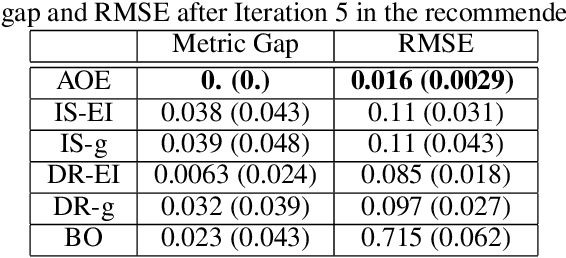
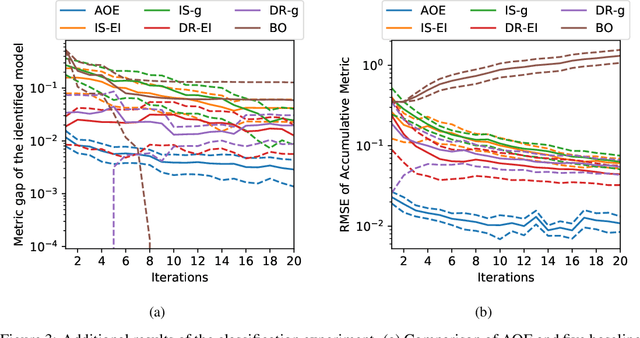
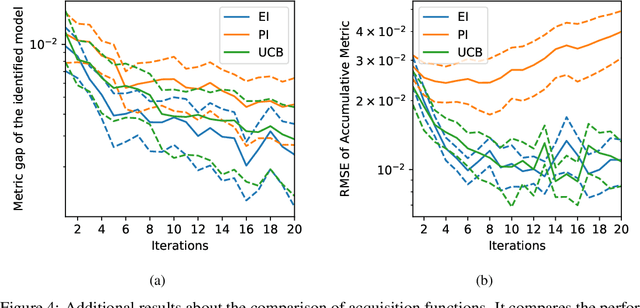
A challenge that machine learning practitioners in the industry face is the task of selecting the best model to deploy in production. As a model is often an intermediate component of a production system, online controlled experiments such as A/B tests yield the most reliable estimation of the effectiveness of the whole system, but can only compare two or a few models due to budget constraints. We propose an automated online experimentation mechanism that can efficiently perform model selection from a large pool of models with a small number of online experiments. We derive the probability distribution of the metric of interest that contains the model uncertainty from our Bayesian surrogate model trained using historical logs. Our method efficiently identifies the best model by sequentially selecting and deploying a list of models from the candidate set that balance exploration-exploitation. Using simulations based on real data, we demonstrate the effectiveness of our method on two different tasks.

Making Differentiable Architecture Search less local

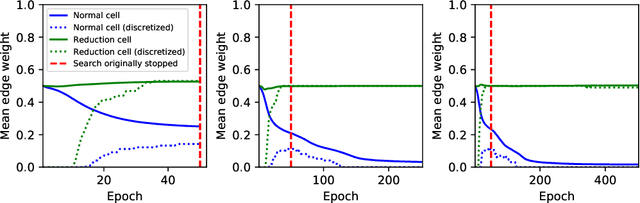
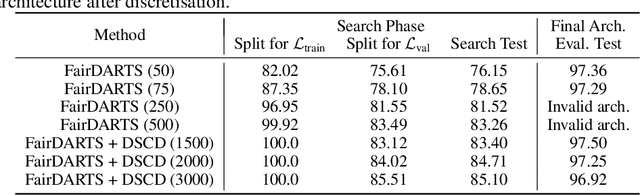
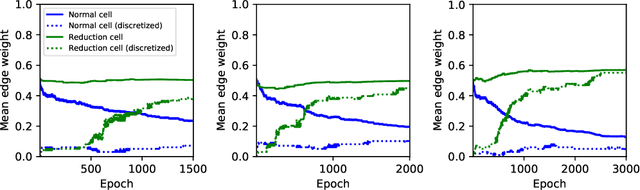
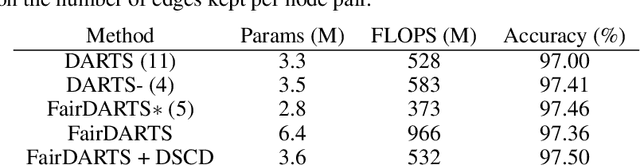
Neural architecture search (NAS) is a recent methodology for automating the design of neural network architectures. Differentiable neural architecture search (DARTS) is a promising NAS approach that dramatically increases search efficiency. However, it has been shown to suffer from performance collapse, where the search often leads to detrimental architectures. Many recent works try to address this issue of DARTS by identifying indicators for early stopping, regularising the search objective to reduce the dominance of some operations, or changing the parameterisation of the search problem. In this work, we hypothesise that performance collapses can arise from poor local optima around typical initial architectures and weights. We address this issue by developing a more global optimisation scheme that is able to better explore the space without changing the DARTS problem formulation. Our experiments show that our changes in the search algorithm allow the discovery of architectures with both better test performance and fewer parameters.

The Evidence Lower Bound of Variational Autoencoders Converges to a Sum of Three Entropies

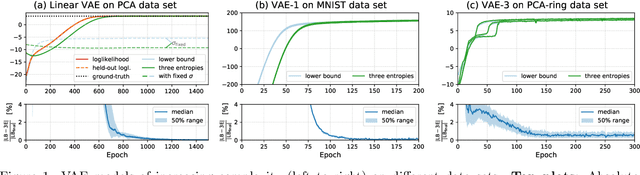
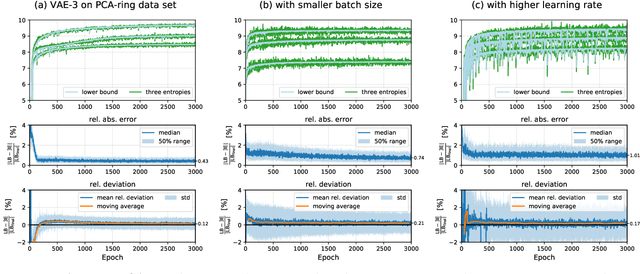
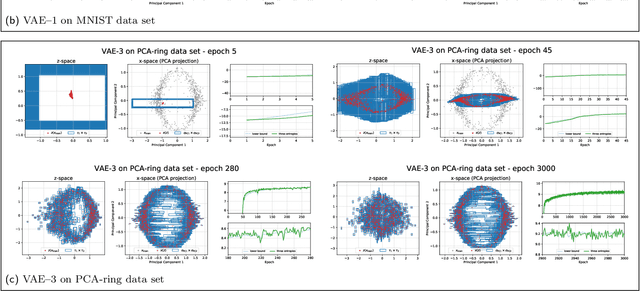
The central objective function of a variational autoencoder (VAE) is its variational lower bound. Here we show that for standard VAEs the variational bound is at convergence equal to the sum of three entropies: the (negative) entropy of the latent distribution, the expected (negative) entropy of the observable distribution, and the average entropy of the variational distributions. Our derived analytical results are exact and apply for small as well as complex neural networks for decoder and encoder. Furthermore, they apply for finite and infinitely many data points and at any stationary point (including local and global maxima). As a consequence, we show that the variance parameters of encoder and decoder play the key role in determining the values of variational bounds at convergence. Furthermore, the obtained results can allow for closed-form analytical expressions at convergence, which may be unexpected as neither variational bounds of VAEs nor log-likelihoods of VAEs are closed-form during learning. As our main contribution, we provide the proofs for convergence of standard VAEs to sums of entropies. Furthermore, we numerically verify our analytical results and discuss some potential applications. The obtained equality to entropy sums provides novel information on those points in parameter space that variational learning converges to. As such, we believe they can potentially significantly contribute to our understanding of established as well as novel VAE approaches.

Black-box density function estimation using recursive partitioning

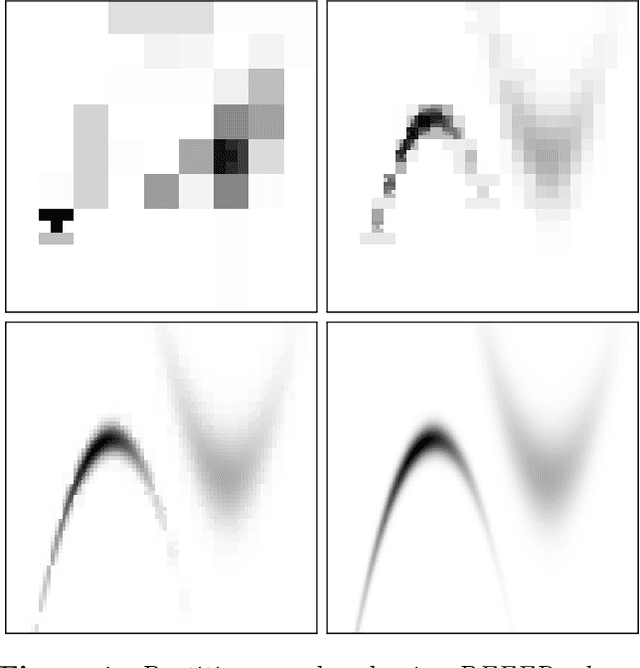
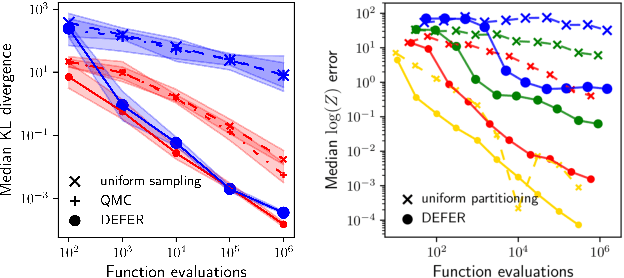
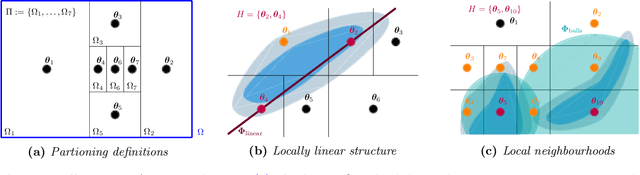
We present a novel approach to Bayesian inference and general Bayesian computation that is defined through a recursive partitioning of the sample space. It does not rely on gradients, nor require any problem-specific tuning, and is asymptotically exact for any density function with a bounded domain. The output is an approximation to the whole density function including the normalization constant, via partitions organized in efficient data structures. This allows for evidence estimation, as well as approximate posteriors that allow for fast sampling and fast evaluations of the density. It shows competitive performance to recent state-of-the-art methods on synthetic and real-world problem examples including parameter inference for gravitational-wave physics.

ProSper -- A Python Library for Probabilistic Sparse Coding with Non-Standard Priors and Superpositions

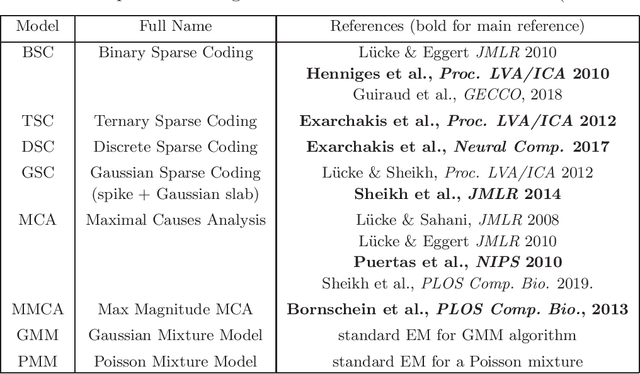
ProSper is a python library containing probabilistic algorithms to learn dictionaries. Given a set of data points, the implemented algorithms seek to learn the elementary components that have generated the data. The library widens the scope of dictionary learning approaches beyond implementations of standard approaches such as ICA, NMF or standard L1 sparse coding. The implemented algorithms are especially well-suited in cases when data consist of components that combine non-linearly and/or for data requiring flexible prior distributions. Furthermore, the implemented algorithms go beyond standard approaches by inferring prior and noise parameters of the data, and they provide rich a-posteriori approximations for inference. The library is designed to be extendable and it currently includes: Binary Sparse Coding (BSC), Ternary Sparse Coding (TSC), Discrete Sparse Coding (DSC), Maximal Causes Analysis (MCA), Maximum Magnitude Causes Analysis (MMCA), and Gaussian Sparse Coding (GSC, a recent spike-and-slab sparse coding approach). The algorithms are scalable due to a combination of variational approximations and parallelization. Implementations of all algorithms allow for parallel execution on multiple CPUs and multiple machines for medium to large-scale applications. Typical large-scale runs of the algorithms can use hundreds of CPUs to learn hundreds of dictionary elements from data with tens of millions of floating-point numbers such that models with several hundred thousand parameters can be optimized. The library is designed to have minimal dependencies and to be easy to use. It targets users of dictionary learning algorithms and Machine Learning researchers.