Evolutionary Variational Optimization of Generative Models

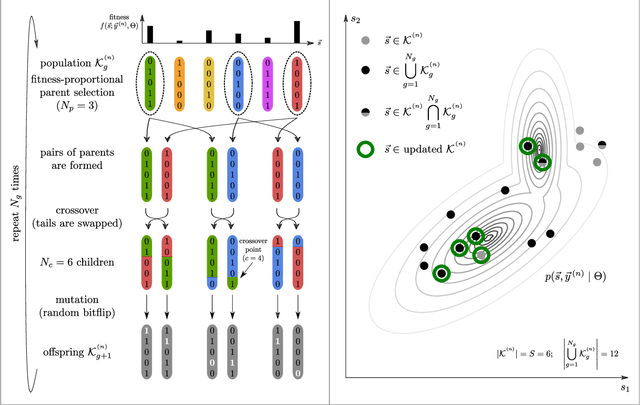
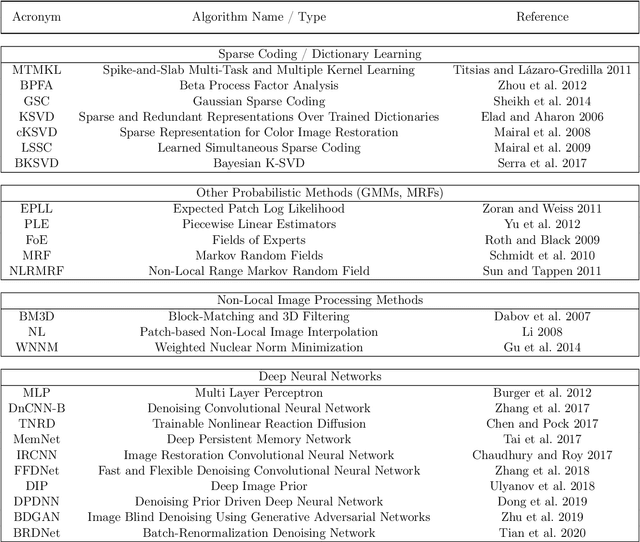
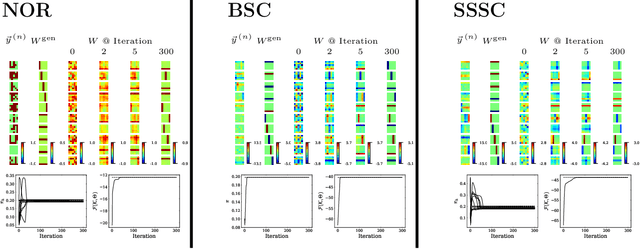
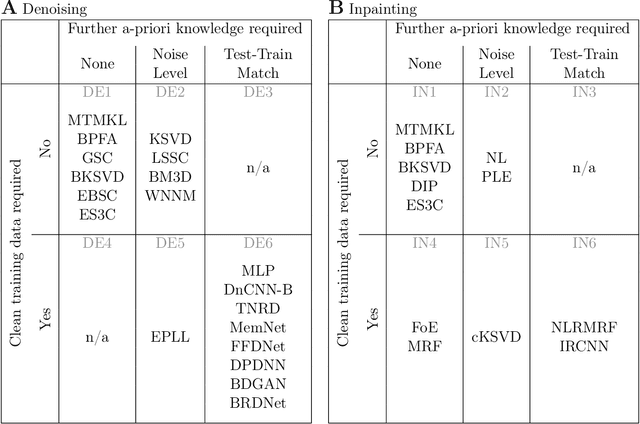
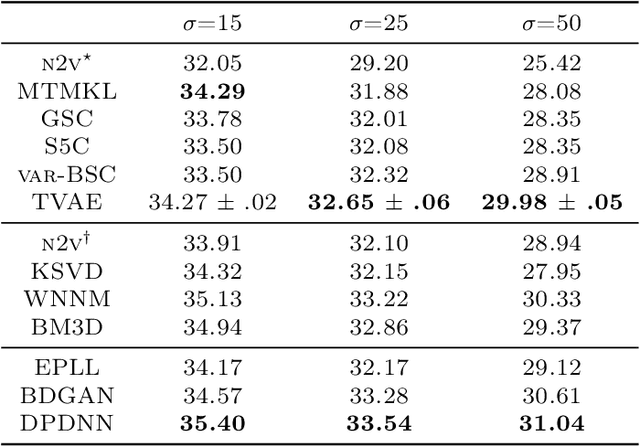
We combine two popular optimization approaches to derive learning algorithms for generative models: variational optimization and evolutionary algorithms. The combination is realized for generative models with discrete latents by using truncated posteriors as the family of variational distributions. The variational parameters of truncated posteriors are sets of latent states. By interpreting these states as genomes of individuals and by using the variational lower bound to define a fitness, we can apply evolutionary algorithms to realize the variational loop. The used variational distributions are very flexible and we show that evolutionary algorithms can effectively and efficiently optimize the variational bound. Furthermore, the variational loop is generally applicable ("black box") with no analytical derivations required. To show general applicability, we apply the approach to three generative models (we use noisy-OR Bayes Nets, Binary Sparse Coding, and Spike-and-Slab Sparse Coding). To demonstrate effectiveness and efficiency of the novel variational approach, we use the standard competitive benchmarks of image denoising and inpainting. The benchmarks allow quantitative comparisons to a wide range of methods including probabilistic approaches, deep deterministic and generative networks, and non-local image processing methods. In the category of "zero-shot" learning (when only the corrupted image is used for training), we observed the evolutionary variational algorithm to significantly improve the state-of-the-art in many benchmark settings. For one well-known inpainting benchmark, we also observed state-of-the-art performance across all categories of algorithms although we only train on the corrupted image. In general, our investigations highlight the importance of research on optimization methods for generative models to achieve performance improvements.

Direct Evolutionary Optimization of Variational Autoencoders With Binary Latents

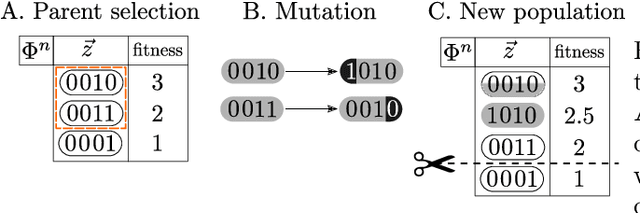
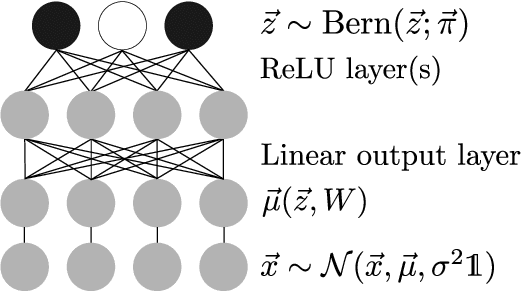
Discrete latent variables are considered important for real world data, which has motivated research on Variational Autoencoders (VAEs) with discrete latents. However, standard VAE-training is not possible in this case, which has motivated different strategies to manipulate discrete distributions in order to train discrete VAEs similarly to conventional ones. Here we ask if it is also possible to keep the discrete nature of the latents fully intact by applying a direct discrete optimization for the encoding model. The approach is consequently strongly diverting from standard VAE-training by sidestepping sampling approximation, reparameterization trick and amortization. Discrete optimization is realized in a variational setting using truncated posteriors in conjunction with evolutionary algorithms. For VAEs with binary latents, we (A) show how such a discrete variational method ties into gradient ascent for network weights, and (B) how the decoder is used to select latent states for training. Conventional amortized training is more efficient and applicable to large neural networks. However, using smaller networks, we here find direct discrete optimization to be efficiently scalable to hundreds of latents. More importantly, we find the effectiveness of direct optimization to be highly competitive in `zero-shot' learning. In contrast to large supervised networks, the here investigated VAEs can, e.g., denoise a single image without previous training on clean data and/or training on large image datasets. More generally, the studied approach shows that training of VAEs is indeed possible without sampling-based approximation and reparameterization, which may be interesting for the analysis of VAE-training in general. For `zero-shot' settings a direct optimization, furthermore, makes VAEs competitive where they have previously been outperformed by non-generative approaches.

Maximal Causes for Exponential Family Observables

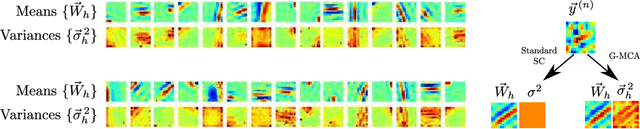
The data model of standard sparse coding assumes a weighted linear summation of latents to determine the mean of Gaussian observation noise. However, such a linear summation of latents is often at odds with non-Gaussian observables (e.g., means of the Bernoulli distribution have to lie in the unit interval), and also in the Gaussian case it can be difficult to justify for many types of data. Alternative superposition models (i.e., links between latents and observables) have therefore been investigated repeatedly. Here we show that using the maximum instead of a linear sum to link latents to observables allows for the derivation of very general and concise parameter update equations. Concretely, we derive a set of update equations that has the same functional form for all distributions of the exponential family (given that derivatives w.r.t. their parameters can be taken). Our results consequently allow for the development of latent variable models for commonly as well as for unusually distributed data. We numerically verify our analytical result assuming standard Gaussian, Gamma, Poisson, Bernoulli and Exponential distributions and point to some potential applications.

ProSper -- A Python Library for Probabilistic Sparse Coding with Non-Standard Priors and Superpositions

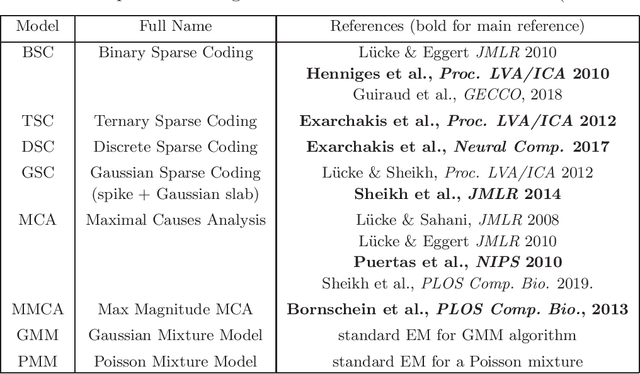
ProSper is a python library containing probabilistic algorithms to learn dictionaries. Given a set of data points, the implemented algorithms seek to learn the elementary components that have generated the data. The library widens the scope of dictionary learning approaches beyond implementations of standard approaches such as ICA, NMF or standard L1 sparse coding. The implemented algorithms are especially well-suited in cases when data consist of components that combine non-linearly and/or for data requiring flexible prior distributions. Furthermore, the implemented algorithms go beyond standard approaches by inferring prior and noise parameters of the data, and they provide rich a-posteriori approximations for inference. The library is designed to be extendable and it currently includes: Binary Sparse Coding (BSC), Ternary Sparse Coding (TSC), Discrete Sparse Coding (DSC), Maximal Causes Analysis (MCA), Maximum Magnitude Causes Analysis (MMCA), and Gaussian Sparse Coding (GSC, a recent spike-and-slab sparse coding approach). The algorithms are scalable due to a combination of variational approximations and parallelization. Implementations of all algorithms allow for parallel execution on multiple CPUs and multiple machines for medium to large-scale applications. Typical large-scale runs of the algorithms can use hundreds of CPUs to learn hundreds of dictionary elements from data with tens of millions of floating-point numbers such that models with several hundred thousand parameters can be optimized. The library is designed to have minimal dependencies and to be easy to use. It targets users of dictionary learning algorithms and Machine Learning researchers.