ConStellaration: A dataset of QI-like stellarator plasma boundaries and optimization benchmarks

Stellarators are magnetic confinement devices under active development to deliver steady-state carbon-free fusion energy. Their design involves a high-dimensional, constrained optimization problem that requires expensive physics simulations and significant domain expertise. Recent advances in plasma physics and open-source tools have made stellarator optimization more accessible. However, broader community progress is currently bottlenecked by the lack of standardized optimization problems with strong baselines and datasets that enable data-driven approaches, particularly for quasi-isodynamic (QI) stellarator configurations, considered as a promising path to commercial fusion due to their inherent resilience to current-driven disruptions. Here, we release an open dataset of diverse QI-like stellarator plasma boundary shapes, paired with their ideal magnetohydrodynamic (MHD) equilibria and performance metrics. We generated this dataset by sampling a variety of QI fields and optimizing corresponding stellarator plasma boundaries. We introduce three optimization benchmarks of increasing complexity: (1) a single-objective geometric optimization problem, (2) a "simple-to-build" QI stellarator, and (3) a multi-objective ideal-MHD stable QI stellarator that investigates trade-offs between compactness and coil simplicity. For every benchmark, we provide reference code, evaluation scripts, and strong baselines based on classical optimization techniques. Finally, we show how learned models trained on our dataset can efficiently generate novel, feasible configurations without querying expensive physics oracles. By openly releasing the dataset along with benchmark problems and baselines, we aim to lower the entry barrier for optimization and machine learning researchers to engage in stellarator design and to accelerate cross-disciplinary progress toward bringing fusion energy to the grid.

Evolutionary Variational Optimization of Generative Models

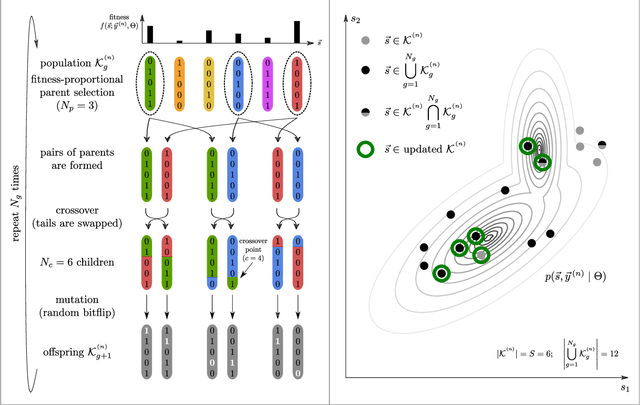
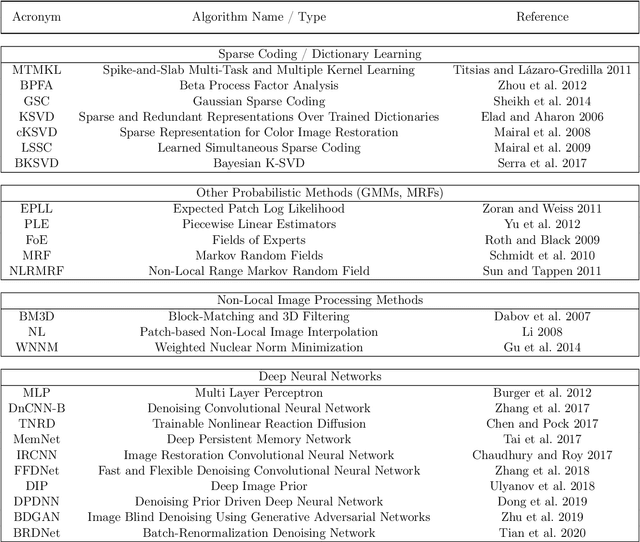
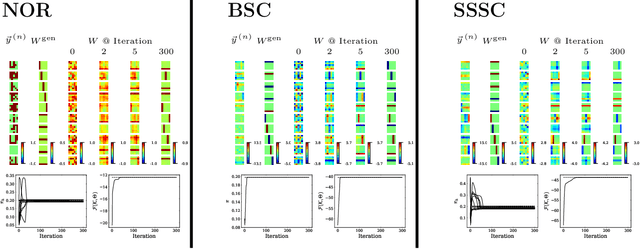
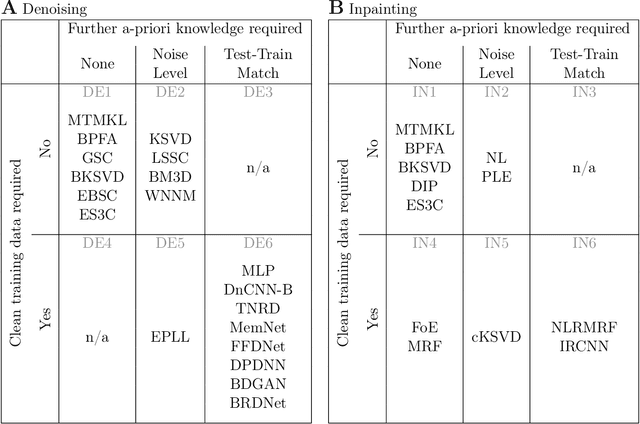
We combine two popular optimization approaches to derive learning algorithms for generative models: variational optimization and evolutionary algorithms. The combination is realized for generative models with discrete latents by using truncated posteriors as the family of variational distributions. The variational parameters of truncated posteriors are sets of latent states. By interpreting these states as genomes of individuals and by using the variational lower bound to define a fitness, we can apply evolutionary algorithms to realize the variational loop. The used variational distributions are very flexible and we show that evolutionary algorithms can effectively and efficiently optimize the variational bound. Furthermore, the variational loop is generally applicable ("black box") with no analytical derivations required. To show general applicability, we apply the approach to three generative models (we use noisy-OR Bayes Nets, Binary Sparse Coding, and Spike-and-Slab Sparse Coding). To demonstrate effectiveness and efficiency of the novel variational approach, we use the standard competitive benchmarks of image denoising and inpainting. The benchmarks allow quantitative comparisons to a wide range of methods including probabilistic approaches, deep deterministic and generative networks, and non-local image processing methods. In the category of "zero-shot" learning (when only the corrupted image is used for training), we observed the evolutionary variational algorithm to significantly improve the state-of-the-art in many benchmark settings. For one well-known inpainting benchmark, we also observed state-of-the-art performance across all categories of algorithms although we only train on the corrupted image. In general, our investigations highlight the importance of research on optimization methods for generative models to achieve performance improvements.

Direct Evolutionary Optimization of Variational Autoencoders With Binary Latents

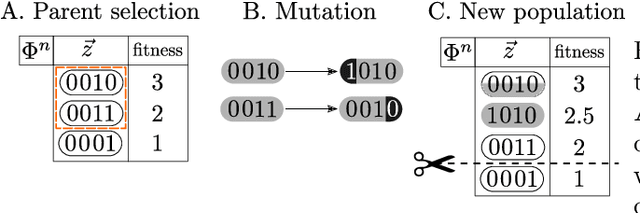
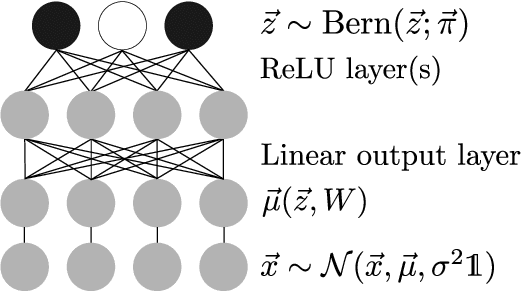
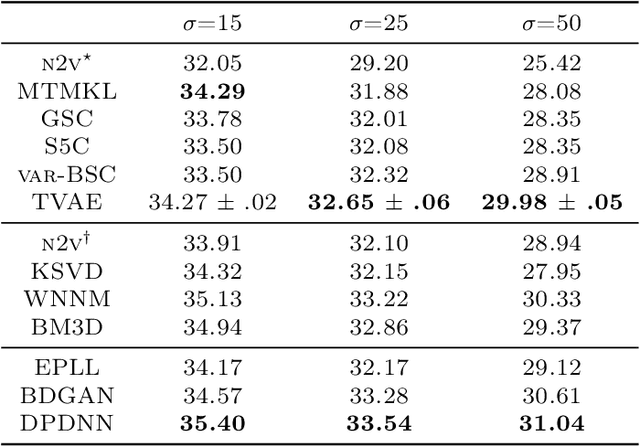
Discrete latent variables are considered important for real world data, which has motivated research on Variational Autoencoders (VAEs) with discrete latents. However, standard VAE-training is not possible in this case, which has motivated different strategies to manipulate discrete distributions in order to train discrete VAEs similarly to conventional ones. Here we ask if it is also possible to keep the discrete nature of the latents fully intact by applying a direct discrete optimization for the encoding model. The approach is consequently strongly diverting from standard VAE-training by sidestepping sampling approximation, reparameterization trick and amortization. Discrete optimization is realized in a variational setting using truncated posteriors in conjunction with evolutionary algorithms. For VAEs with binary latents, we (A) show how such a discrete variational method ties into gradient ascent for network weights, and (B) how the decoder is used to select latent states for training. Conventional amortized training is more efficient and applicable to large neural networks. However, using smaller networks, we here find direct discrete optimization to be efficiently scalable to hundreds of latents. More importantly, we find the effectiveness of direct optimization to be highly competitive in `zero-shot' learning. In contrast to large supervised networks, the here investigated VAEs can, e.g., denoise a single image without previous training on clean data and/or training on large image datasets. More generally, the studied approach shows that training of VAEs is indeed possible without sampling-based approximation and reparameterization, which may be interesting for the analysis of VAE-training in general. For `zero-shot' settings a direct optimization, furthermore, makes VAEs competitive where they have previously been outperformed by non-generative approaches.